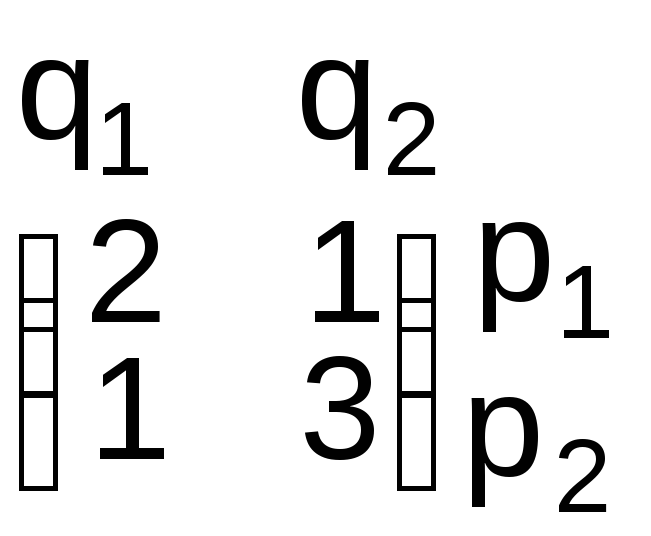Графический способ решения матричной игры

Найдем графическим методом решение следующей матричной игры:

Данная матричная игра неразрешима в чистых стратегиях.

Графически решается задача игрока, имеющего две стратегии, т.е. в данном случае первого игрока. Оптимальная стратегия второго игрока находится аналитическим путем после решения задачи первого игрока.

Максминная стратегия первого игрока находится путем решения следующей задачи первого игрока:

Идея графического метода состоит в том, что функция , показывающая минимальные (гарантированные) выигрыши первого игрока при всевозможных его смешанных стратегиях р, строится графически. График этой функции называется нижней границей выигрышей первого игрока. Затем на нижней границе находится точка, соответствующая максимальному выигрышу первого игрока.

Графические построения осуществляются следующим образом.

На горизонтальной прямой берется отрезок единичной длины. Каждой точке этого отрезка сопоставляется смешанная стратегия первого игрока по следующему правилу:

р₁ - это расстояние от точки до правого конца отрезка, а р₂ - расстояние от точки до левого конца отрезка (рис. 1).

Любой смешанной стратегии первого игрока на единичном отрезке будет отвечать некоторая единственная точка, найденная по указанному правилу. Таким образом, между точками отрезка и смешанными стратегиями первого игрока устанавливается взаимно однозначное соответствие.

Затем к концам единичного отрезка проводятся две вертикальные прямые. На левой вертикальной прямой откладываются выигрыши первого игрока, соответствующие первой его чистой стратегии (значения элементов первой строки платежной матрицы А), а на правой вертикальной прямой - выигрыши, соответствующие второй его стратегии (значения элементов второй строки матрицы А). Положительные значения элементов откладываются на прямых вверх от единичного отрезка, а отрицательные - вниз. Точки, соответствующие элементам одного столбца матрицы (стратегии второго игрока), соединяются отрезками с указанием их номеров (номеров соответствующих столбцов) (рис.2).

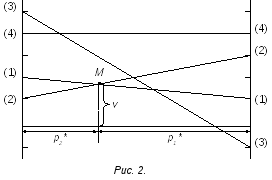
На рис. 2 - это четыре отрезка, соответствующие чистым стратегиям второго игрока.

Находим теперь нижнюю границу выигрышей первого игрока в виде ломаной линии, огибающей снизу все эти отрезки (эта граница показана жирной линией).

Расстояние от любой точки, расположенной на нижней границе до ближайшей точки единичного отрезка, взятое с учетом знака ("+", если точка границы находится выше единичного отрезка и "-", если она расположена ниже единичного отрезка), характеризует тот выигрыш, который гарантирован первому игроку в случае выбора им смешанной стратегии .

Другими словами, это расстояние совпадает с величиной , к максимизации которой стремится первый игрок.

Решение задачи первого игрока сводится, таким образом, к отысканию на нижней границе его выигрышей точки, соответствующей наибольшему выигрышу, т.е. наиболее удаленной точки от единичного отрезка. На рис. 2 - это точка М, находящаяся на пересечении первого и второго отрезков. Первая и вторая чистые стратегии второго игрока называются активными, и он их должен использовать в своей оптимальной стратегии с ненулевой вероятностью. Третий же и четвертый отрезки не проходят через точку М, поэтому третья и четвертая стратегии, наоборот, называются пассивными – второй игрок не должен их использовать в оптимальной стратегии.

Далее определяются графически цена игры v как расстояние от точки М до единичного отрезка (взятое с учетом знака) и оптимальная смешанная стратегия .

Так как графическое определение числовых значений этих величин является довольно грубым, то следует уточнить их аналитически путем решения системы линейных уравнений. При составлении систем уравнений для нахождения оптимальных стратегий игроков используются лишь два столбца матрицы А, соответствующие активным стратегиям второго игрока, т.е. матрица

(1)

При составлении системы уравнений для первого игрока столбцы этой матрицы умножаются скалярно на столбец неизвестных .

Приравнивая эти значения к цене игры v и добавляя уравнение , получим следующую систему линейных уравнений для определения вектора и величины v:

(2)

Вычитая из первого уравнения системы второе, получим уравнение , откуда .

С учетом третьего уравнения находим , . Для определения величины v можно использовать либо первое, либо второе уравнение системы. Беря первое, получим:

Найдем теперь оптимальную стратегию второго игрока. Как уже отмечалось, третья и четвертая стратегии его являются пассивными, поэтому . Остальные компоненты вектора находятся аналитически путем решения системы уравнений, составляемых также на основе приведенной матрицы (1).

При составлении системы для второго игрока строчки матрицы скалярно умножаются на строку неизвестных .

Приравнивая результаты умножения к цене игры v и добавляя уравнение , получим систему уравнений:

(3)

Так как значение v уже известно, для определения неизвестных достаточно взять какие-либо два уравнения этой системы. Возьмем, например, первое и третье уравнения:

откуда находим ,

В итоге получим следующее оптимальное решение игры в смешанных стратегиях и ее цену:

Ниже показаны некоторые из возможных картинок, которые могут получиться при графическом решении игры. На рис. 3а точка М расположена ниже единичного отрезка, поэтому цена игры v будет отрицательной. На рис. 3б показана игра с нулевой ценой, а на рис. 3в – игра, имеющая множество оптимальных решений. Любой точке отрезка М₁М₂ нижней границы соответствует оптимальная смешанная стратегия первого игрока.

В некоторых задачах раздела необходимо найти оптимальную игру с платежной матрицей размером m2, т.е. когда у второго игрока две стратегии. В этом случае графически решается задача второго игрока (находится минимаксная его стратегия).

Пусть, например, задана следующая платежная матрица

В этой игре необходимо найти оптимальные стратегии , соответственно первого и второго игроков и цену игры v.

Оптимизационная задача второго игрока такова:

и она решается путем построения графика функции и отыскания на нем точки минимума.

Так же выбирается отрезок единичной длины на горизонтальной прямой и к его концам проводятся перпендикулярные прямые. Здесь каждой точке единичного отрезка ставится в соответствие смешанная стратегия второго игрока, где - это расстояние от точки до правого конца отрезка, a - расстояние до левого конца.

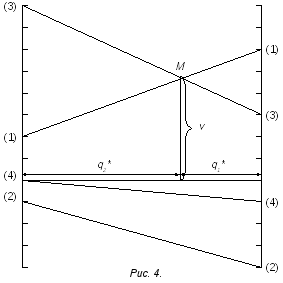
На левой вертикальной прямой откладываются проигрыши второго игрока, соответствующие первой его стратегии (элементы первого столбца), а на правой прямой - проигрыши, соответствующие второй стратегии (элементы второго столбца). Отрезками соединяются точки, соответствующие элементам одной и той же строки (стратегии первого игрока).

На рис. 4 показан результат такого графического построения.

Находим верхнюю границу проигрышей второго игрока (ломаную линию, огибающую сверху построенные отрезки) и на этой границе - точку минимума М.

Графически определяем цену игры v и оптимальную смешанную стратегию второго игрока.

Далее аналитически уточняем эти величины и определяем .оптимальную стратегию первого игрока.

Так как точка М находится на пересечении первого и третьего отрезков, то при составлении систем уравнений используются первая и третья строки матрицы А, т.е. матрица:

Тогда:

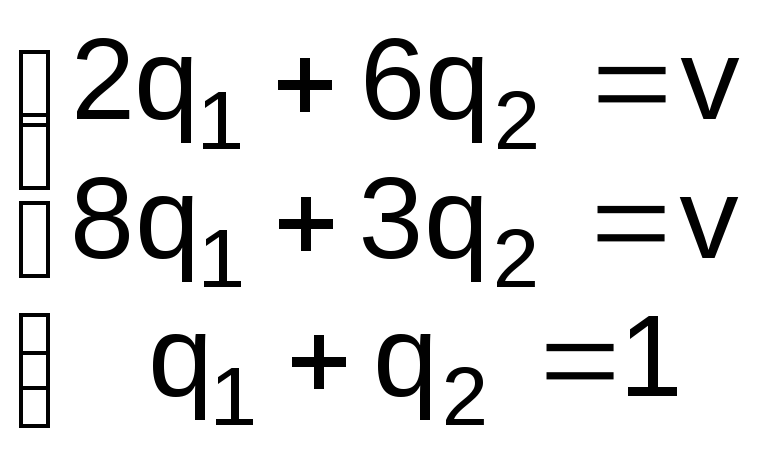
Решая эти системы, получим следующий ответ: