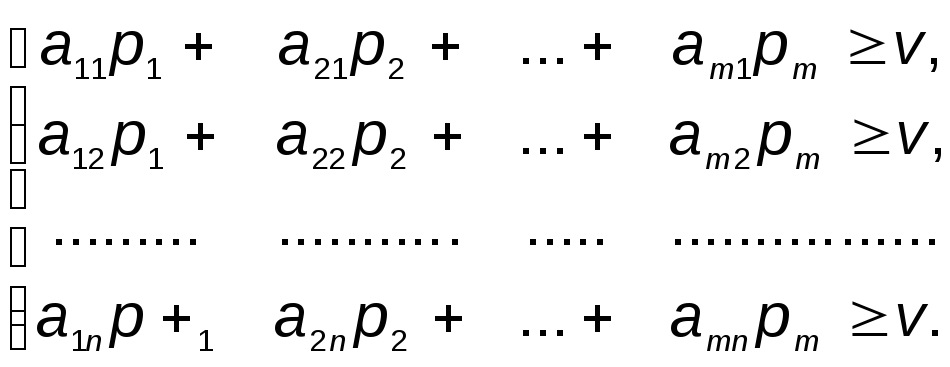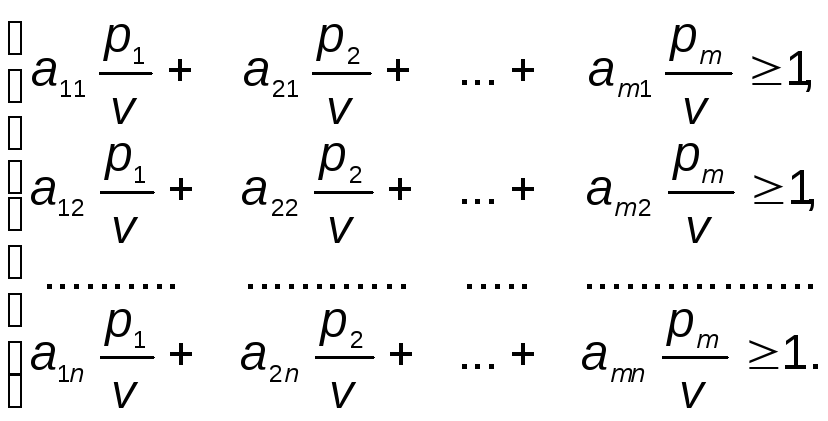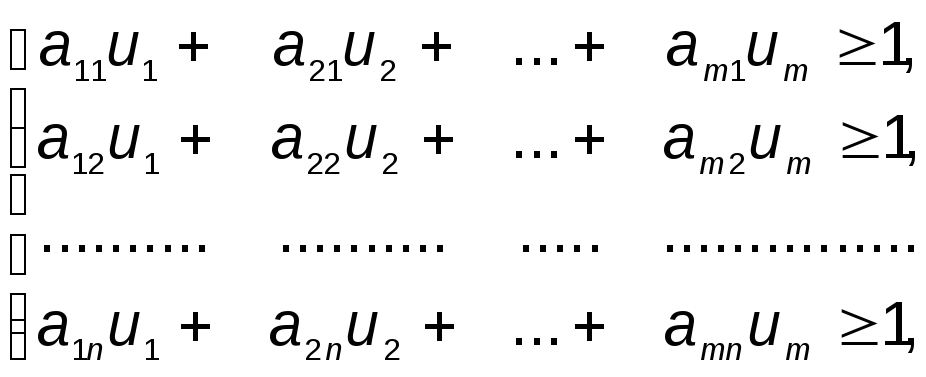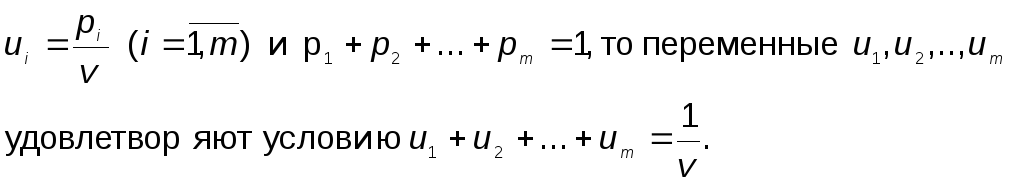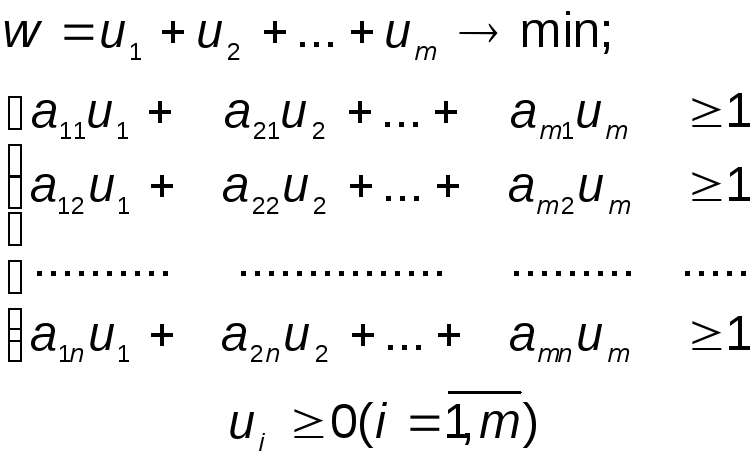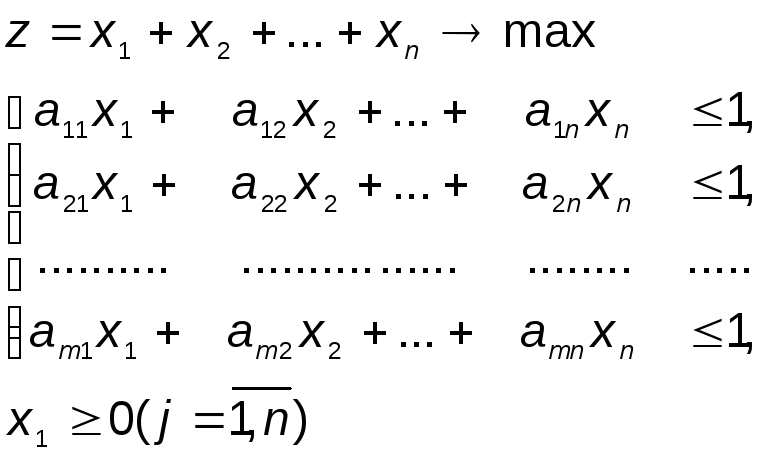11.3.Решение игры без седловой точки

Игры с седловой точкой встречаются редко. Большинство игр седловой точки не имеют. К ним относится и рассмотренная игра полковника Блотто.

Если седловая точка отсутствует, то игрок А, применяя свою максиминную стратегию, выиграет не менее v₁, а игрок В, применяя свою минимаксную стратегию, проиграет не более v₂, где v₁< v₂. Применение чистых стратегий в каждой партии такой игры не дает возможности игрокам увеличить выигрыш (v₁) или уменьшить проигрыш (v₂). Для того чтобы это было возможно, необходимо применять не одну, а несколько чистых стратегий, чередуя их случайным образом с какими-то частотами. Такая стратегия получила название смешанной стратегии. Ее элементами являются чистые стратегии.

В одной партии одноходовой игры игрок может использовать только одну чистую стратегию. Поэтому смешанная стратегия имеет смысл при условии, что игра состоит более чем из одной партии. Перед каждой партией игрок выбирает стратегию некоторым случайным образом, например бросает жребий и применяет ту стратегию, которая выпала.

Поведение игрока, при котором он с определенной частотой или вероятностью случайно чередует все свои чистые стратегии, называется смешанной стратегией.

Обозначим смешанную стратегию игрока I как:

(9)

а смешанную стратегию игрока II как:

(10)

где:

p_i - вероятность выбора игроком I i-й чистой стратегии;

q_j - вероятность выбора игроком II j-й чистой стратегии.

Результаты использования игроками смешанных стратегий p и q оцениваются с помощью функций выигрыша (платежной функции):

(11)

выражающей математическое ожидание выигрыша игрока I и соответственного проигрыша игрока II.

Для матричных игр справедлива следующая теорема Неймана:

Любая матричная игра имеет оптимальное решение в смешанных стратегиях.

Лишь в некоторых случаях оптимальное решение игры возможно в чистых стратегиях, когда оба игрока применяют в каждой партии одну чистую стратегию с единичной вероятностью, а остальные с нулевой вероятностью. Такое может быть только в играх с платежными матрицами, обладающими специальным свойством - седловой точкой.

Чистые стратегии игроков А и В, для которых вероятность p_i и q_j отличны от нуля, называются активными. В частном случае, когда все вероятности, кроме одной равны нулю, а эта одна равна единице, смешанная стратегия превращается в чистую.

Решение игры, не имеющей седловой точки, может осуществляться различными методами. Рассмотрим некоторые из них.

1. Чаще всего матричная игра решается путем сведения ее к задаче линейного программирования. Эта задачи могут быть решена, например, симплекc-методом и, следовательно, найдено решение игры.

2. Известны несколько методов приближенного решения матричной игры, например, метод Брауна.

3. Если матица игры имеет размерность, равную двум (у одного из игроков имеется только две стратегии), то решение игры может быть получено графически.

Решение матричной игры с помощью симплекс-метода

Пусть имеется игра с платежной матрицей порядка (mn) без седловой точки. В предыдущем изложении обращалось внимание на сложность решения задач математического программирования большой размерности. Поскольку игра сводится к задаче линейного программирования, прежде чем заниматься этим, игру необходимо упростить, избавившись от лишних стратегий.

Лишние стратегии бывают двух видов: дублирующие и заведомо невыгодные. Рассмотрим процесс упрощения на примере игры, приведенной в табл. 3.

Таблица 3

Вj Аi	В1	В2	В3	В4
А1	2	4	8	6
А2	1	4	6	4
А3	2	4	8	6
А4	8	6	2	1

Вначале займемся стратегиями игрока А. Анализ матрицы игры показывает, что стратегия А₃ дублирует стратегию А₁. Поэтому стратегию А₃ (или А₁) можно исключить из рассмотрения. Далее, в строке А₁ все выигрыши больше (или равны) выигрышам в соответствующих столбцах строки А₂ (А₁ доминирует над А₂). Значит, для игрока А стратегия А₂ невыгодна по сравнению со стратегией А₁. Стратегию А₂ можно также исключить. После первого этапа упрощения игра примет вид, отраженный в табл. 4.

Теперь займемся стратегиями игрока В. Проанализируем игру, представленную табл. 4. В столбце В₃ все проигрыши больше проигрышей в соответствующих строках столбца В₄ (В₄ доминирует над В₃). Следовательно, для игрока В стратегия В₃ невыгодна по сравнению с В₄. Стратегию В₃ можно исключить из рассмотрения. Окончательно игра примет вид, представленный табл. 5.

Таблица 4						Таблица 5
Вj Аi	В1	В2	В3	В4		Вj Аi	В1	В2	В4
А1	2	4	8	6		А1	2	4	6
А4	8	6	2	1		А4	8	6	1

В результате проведенных упрощений игра с платежной матрицей 4-го порядка сведена к игре с платежной матрицей порядка 2х3.

Опишем теперь как матричная игра сводится к задаче линейного программирования.

Допустим, что все элементы a_ij платежной матрицы положительны. Этого можно добиться, добавив ко всем членам матрицы большое число М. От этого цена игры (v) увеличится на М, а решение p^*, q^* не изменится. Если все a_ij положительны, то и цена игры v>0. Необходимо найти решение игры, т.е. две оптимальные смешанные стратегии p*=(p₁, p₂,...p_m) и q*=(q₁, q₂,... q_n), дающие каждому игроку максимально возможный для него средний выигрыш (минимально возможный средний проигрыш). Найдем сначала p*. Известно, что игрок А, применяя свою оптимальную стратегию, не может сделать свой выигрыш меньше v, даже если игрок В применяет любые стратегии. На основании этого получим:

(12)

Разделим обе части каждого неравенства на положительную величину v:

(13)

Введем следующие обозначения:

(14)

Тогда система (13) примет вид:

(15)

где

Так как

Величина v - это гарантированный выигрыш игрока А. Его нужно сделать максимальным, а следовательно, величину - минимальной, т.е. если

Таким образом, решение игры свелось к следующей задаче. Найти неотрицательные значения переменных u₁, u₂, u₃,..., u_m, такие, чтобы они удовлетворяли линейным ограничениям - неравенствам и обращали в минимум линейную функцию этих переменных, а именно:

(16)

Задача (2) является задачей линейного программирования. Определив значения u₁, u₂, ... u_m, можно найти значения p₁, p₂, ... p_m, v, а значит, и оптимальную стратегию p*.

Оптимальная стратегия (q*) игрока В находится аналогично. Только игрок В стремится минимизировать свой проигрыш (v) и, следовательно, величина должна максимизироваться, а ограничения будут иметь вид “”.

Для игрока В задача линейного программирования будет выглядеть следующим образом:

(17)

Задачи (16) и (17) представляют собой пару двойственных задач. На основании первой основной теоремы действенности min w = max z. Следовательно, получим одинаковые цены игры, т.е. седловую точку.