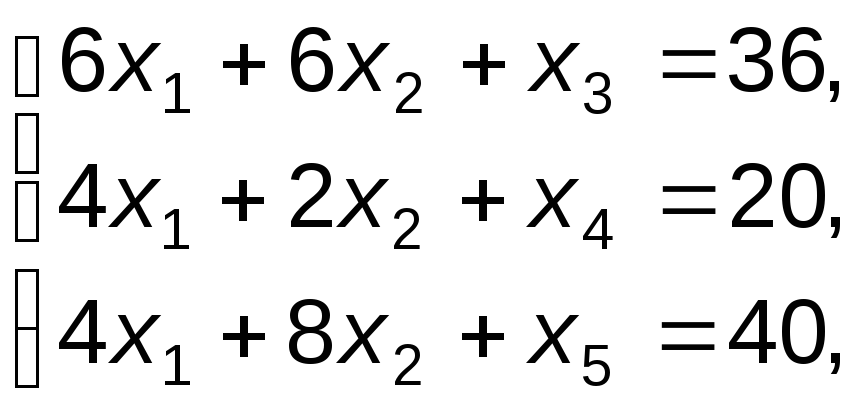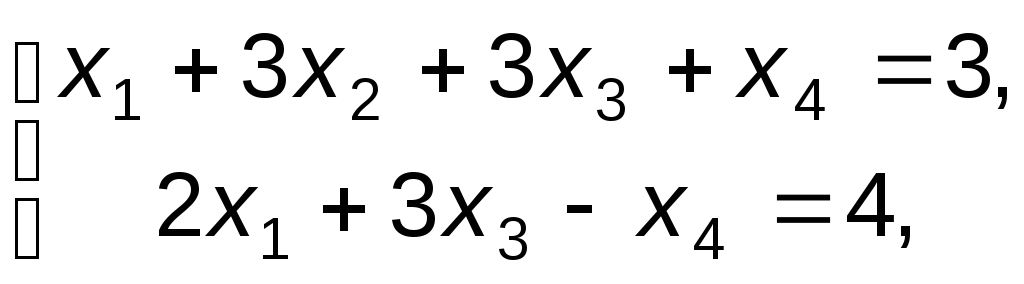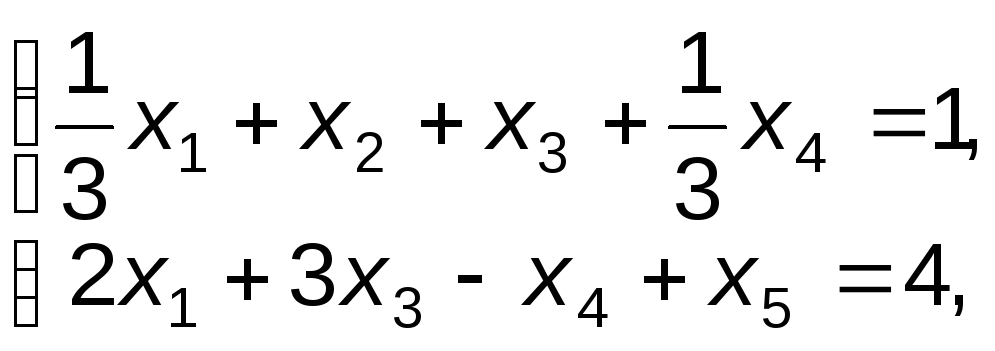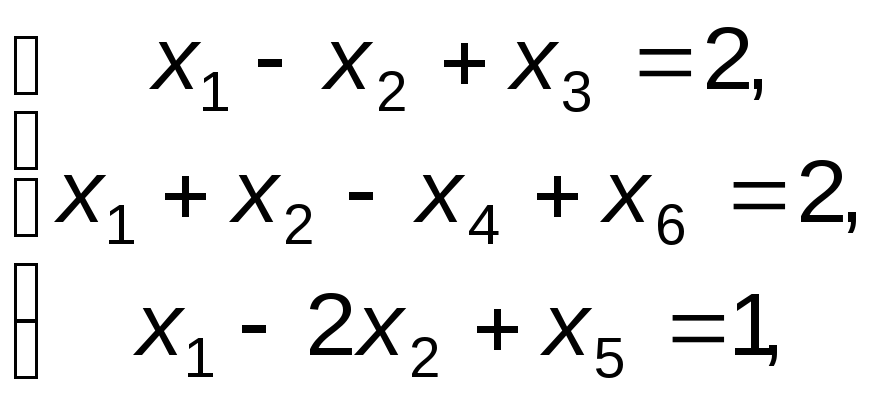5.10.Примеры решения задач линейного программирования симплекс-методом

Пример 1. Рассмотрим задачу об использовании ресурсов (1), постановка которой приведена в § 5.2. Эта задача была решена графическим методом (§ 5.5.), на примере этой задачи был показан процесс нахождения оптимального плана (§ 5.6). Теперь решим эту задачу, применяя алгоритм симплекс-метода.

Модель задачи имеет вид:

f=12x1+15x2  max; x10, x20.

Решение. Приведем задачу к канонической форме:

f=12x1+15x2+0 x3+0 x4+0 x5  max;

Выделяем базисные переменные. Количество базисных переменных должно быть равно количеству ограничений, т.е. трем. В каждом ограничении данной задачи можно выделить одну переменную, которая присутствует только в этом ограничении с коэффициентом +1. Следовательно, переменные x₃, x₄, x₅ являются базисными, а переменные x₁, x₂ - небазисными.

Определим исходный базисный план и значение целевой функции: x₁=0, x₂=0, x₃=36, x₄=20, x₅=40, f=0.

Исходные данные задачи, а также вычисленные по формуле (22) значения целевой функции (f=(-1) 0+0 36+0 20+0 40=0) и по формуле (23) значения относительных оценок (₁=(-1)  12+0 6+0 4+0 4=-12; ₂=(-1)  15+0 6+0 2+0 8=-15) перенесем в исходную симплексную таблицу (табл. 4).

Проверяем полученный план на оптимальность по условию оптимальности (_j0). Поскольку для данного плана существуют оценки ₁<0 и ₂<0, план не является оптимальным. Необходим переход к другому базисному плану.

В первую очередь среди небазисных переменных на основании (24) выберем переменную, которая будет вводиться в базис:

В базис будет вводиться переменная x₂, так как этой переменной соответствует максимальная по модулю относительная оценка =15. Столбец, отвечающий переменной x₂, является главным.

Далее на основании (25) выберем переменную, которая будет выводиться из базиса:

Из базиса будет выводиться переменная x₅, так как этой переменной соответствует минимальное отношение, равное 5. Строка, отвечающая переменной x₅, является главной.

Таблица 4								Таблица 5
Базис	-1	0	12	15			Базис		-1	0	12	0
	С	В	x1	x2					C	B	x1	x5
x3	0	36	6	6			x3		0	6	3	-3/4
x4	0	20	4	2			x4		0	10	3	-1/4
x5	0	40	4	8			x2		15	5	1/2	1/8
		0	-12	-15						75	-9/2	15/8

На пересечении главной строки и главного столбца стоит главный элемент, равный 8. В таблице для удобства расчетов главный элемент необходимо пометить.

Строим новую симплексную таблицу (табл. 5), в которой переменные x₅ и x₂ меняются местами, вместе со своими коэффициентами в целевой функции. Остальные переменные переписываются без изменений со своими коэффициентами.

Пересчитываем элементы табл. 4 и результаты заносим в соответствующие клетки табл. 5. Элементы главной строки табл. 4 пересчитываются путем деления каждого элемента этой строки на главный , главный элемент - путем деления единицы на главный элемент , элементы главного столбца - путем деления каждого элемента этого столбца на главный со знаком минус .

Все остальные элементы табл. 5 определяются по правилу прямоугольника. Например, для клетки x₃x₁ новый элемент равен .

Проверяем правильность расчета значений целевой функции f и оценок ₁, ₅ по формулам (22), (23):

f=(-1) 0+0 6+0 10+15 5=75, , .

Полученный в табл. 5 план не является оптимальным, так как существует . В число базисных вводится переменная x₁, а из базиса исключается переменная x₃.

Пересчитываем элементы табл. 5 и результаты заносим в табл. 6.

Таблица 6
Базис	-1	0	0	0
	С	В	x3	x5
x1	12	2	1/3	-1/4
x4	0	4	-1	1/2
x2	15	4	-1/6	1/4
		84	3/2	3/4

После проверки правильности расчета f и оценок ₃, ₅ делаем вывод о том, что полученный в табл. 6 план является оптимальным, так как оценки ₃, ₅ > 0.

Для получения максимального дохода в размере 84 ед., предприятию необходимо выпускать из имеющихся в наличии ресурсов 2 ед. продукции вида Р₁ и 4 ед. продукции Р₂.Ответ: x*₁=2, x*₂=4, f=84.

Пример 2. Рассмотрим решение задачи линейного программирования симплекс-методом, в которой для построения исходного плана применяется метод искусственного базиса:

f=x1-5x2-x3+x4  max; .

Решение. Исходная задачи записана в канонической форме. Для выделения базисных переменных обе части первого ограничения разделим на 3 и тогда в качестве базисной можно взять переменную x₂, а во второе ограничение введем искусственную переменную x₅:

f=x1-5x2-x3+x4-М x5  max; .

Определим исходный базисный план и значение целевой функции:

x1=0, x3=0, x4=0, x2=1, x5=4, f=-4M.

Заполним исходную симплексную таблицу (табл. 7). При проверке плана на оптимальность для выбора наибольшей по абсолютной величине относительной оценки достаточно рассматривать ту часть отрицательных _j, которая содержит М (в силу того что М – очень большое положительное число).

Таблица 7

Базис	-1	0	1	-1	1
	С	В	x1	x3	x4
x2	-5	1	1/3	1	1/3
x5	-М	4	2	3	-1
		-4М-5	-2М-8/3	-3М-4	М-8/3

Только при наличии нескольких одинаковых наибольших по абсолютной величине частей _j, содержащих М, рассматривается та часть _j, которая М не содержит.

Анализ табл. 7 показывает, что в базис вводится переменная x₃, а выводится - x₂. Пересчитываем элементы табл. 7 по известным формулам. Дальнейшее решение задачи показано в табл. 8-10. Поскольку в табл. 8 из базиса исключается искусственная переменная x₅, то соответствующий ей столбец в новую симплексную таблицу не включается.

Таблица 8

Базис	-1	0	1	-5	1
	С	В	x1	x2	x4
x3	-1	1	1/3	1	1/2
x5	-М	1	1	-3	-2
		-М-1	-М-4/3	3М+4	2М-4/3

Таблица 9

Базис	-1	0	-5	1
	С	В	x2	x4
x3	-1	2/3	2	1
x1	1	1	-3	-2
		1/3	0	-4

Таблица 10

Базис	-1	0	-5	1
	С	В	x2	x3
x4	1	2/3	2	1
x1	1	7/3	1	2
		3	8	4

Полученный в табл. 10 план является оптимальным, так как искусственные переменные в базисе отсутствуют и относительные оценки ₂, ₃>0.

Ответ:

Пример 3. Рассмотрим процесс решения задачи линейного программирования, имеющей бесконечное число планов (решений):

f=x1+x2  min x10, x20.

Решение данной задачи графическим методом приведено в §5.5 (см. рис. 5).

Решение. После приведения задачи к канонической форме для получения исходного базисного плана во второе ограничение введем искусственную переменную x₆. Тогда модель задачи примет следующий вид:

f=-x1-x2+0 x3+0 x4+0 x5-M x6 max .

Процесс получения оптимального плана показан в табл. 11-13. Оптимальный план соответствующий точке А (см. рис. 5), получен в табл. 12, так как ₁=0 и ₄=1. Наличие в оптимальном плане оценки ₁=0 говорит о том, что задача имеет бесконечное число решений. Включение в число базисных переменной x₁, которой отвечает оценка ₁=0, и исключение из базиса переменной x₅ не изменит значения целевой функции, но приведет к изменению базисного плана. Это произойдет на следующей итерации (табл. 13), в результате которой получается новый оптимальный план: f_min=2, соответствующий точке В (см. рис. 5).

Таблица 11

Базис	-1	0	-1	-1	0
	С	В	x1	x2	x4
x3	0	2	1	-1	0
x6	-М	2	1	1	-1
x5	0	1	1	-2	0
		-2М	-М+1	-М+1	М

Таблица 12

Базис	-1	0	-1	0
	С	В	x1	x4
x3	0	4	2	-1
x2	-1	2	1	-1
x5	0	5	3	-2
		-2	0	1

Таблица 13

базис	-1	0	0	0
	С	В	x5	x4
x3	0	2/3	-2/3	1/3
x2	-1	1/3	-1/3	-1/3
x1	-1	5/3	1/3	-2/3
		-2	0	1

Ответ. Оптимальные решения данной задачи будут лежать на отрезке, заключенном между точками А(0, 2) и В. В любой точке этого отрезка целевая функция f_min=2. Задача имеет бесконечное число решений. Координаты любой внутренней точки отрезка АВ могут быть найдены из следующих соотношений :

При =1 получаем координаты точки А, при =0 - координаты точки В.

Замечание. При решении практических задач наличие бесконечного числа оптимальных планов дает возможность выбирать такой план, который в наибольшей степени отвечает сложившейся производственной ситуации.