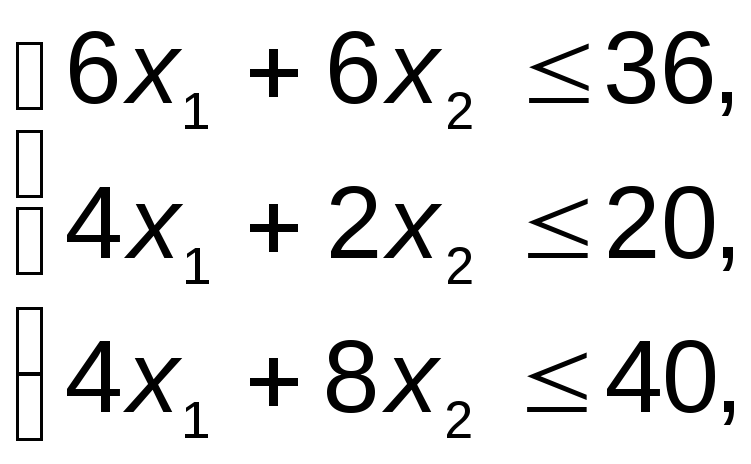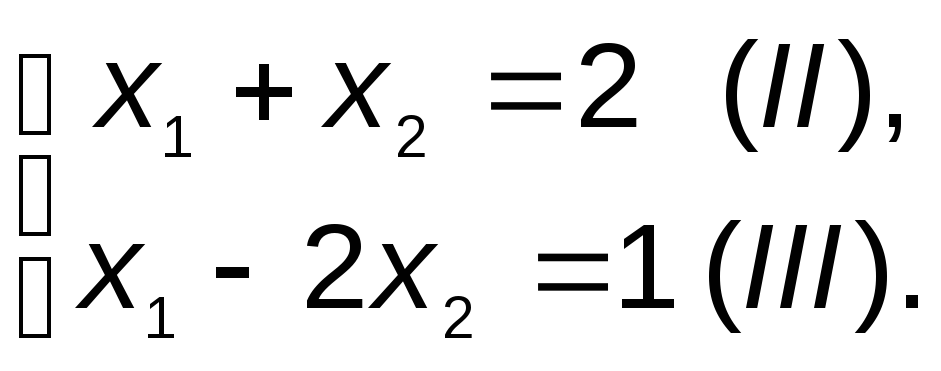- •Содержание
- •Введение
- •Тема 1. Экономико-математические методы и модели и их классификация
- •1.1. Социально-экономические системы, методы их исследования и моделирования
- •1.2.Этапы экономико-математического моделирования, классификация экономико-математических моделей и методов
- •Примеры описательных моделей
- •Тема 2. Балансовый метод в экономике
- •2.1. Общие понятия балансового метода, принципиальная схема межпродуктового баланса
- •2.2. Экономико-математическая модель межотраслевого баланса
- •2.3. Плановые расчеты на основе матричных моделей систем производства и распределения продукции
- •2.3.1. Методика расчета планового баланса по заданным валовым выпускам продукции Xiпл
- •2.3.2. Коэффициенты полных материальных затрат и методы их расчета
- •2.3.3. Методика расчета планового баланса по заданным плановым уровням конечной продукции Yiпл
- •2.4. Пример расчета планового баланса для трехотраслевой экономической системы
- •2.5. Использование балансового метода на предприятии
- •Тема 3. Математические методы сетевого планирования и управления
- •3.1. Основные понятия сетевой модели
- •Распределение (расслоение) вершин сетевого графика по рангам
- •3.2. Анализ сетевого графика и расчет его временных характеристик
- •3.2.1. Расчет временных характеристик событий
- •3.2.2. Расчет временных характеристик работ
- •3.3. Сетевое планирование в условиях неопределенности
- •Вероятностные оценки продолжительности работ
- •3.4. Оптимизация сетевой модели
- •Краткая характеристика метода оптимизации
- •Тема 4. Классификация задач математического программирования и область их эффективного применения в экономике
- •4.1. Математическая постановка и структура задачи оптимизации
- •4.2. Краткая классификация методов математического программирования
- •Тема 5. Линейное программирование
- •5.1. Предмет линейного программирования
- •5.2. Построение оптимизационных моделей для решения экономических задач
- •5.3. Общая задача линейного программирования. Основные определения
- •5.4. Графический метод решения задач линейного программирования
- •I этап. Графическая интерпретация области допустимых решений
- •II этап. Графическая интерпретация целевой функции
- •III этап. Нахождение оптимального решения
- •5.5. Примеры решения задач линейного программирования графическим методом
- •5.6. Понятие о симплекс-методе озлп
- •5.7. Каноническая форма задач линейного программирования
- •5.8. Базисные решения задачи линейного программирования
- •5.9. Алгоритм симплекс-метода озлп
- •5.10.Примеры решения задач линейного программирования симплекс-методом
- •Тема 6. Двойственность в линейном программировании
- •6.1.Понятие двойственности. Построение двойственных задач и их свойства
- •6.2. Основные теоремы двойственности и их экономическое содержание
- •Первая теорема двойственности
- •Вторая теорема двойственности (теорема о дополняющей нежесткости)
- •6.3.Экономическая интерпретация двойственной задачи Пример 1. Задача оптимального использования ресурсов.
- •6.4.Экономико-математический анализ полученных оптимальных решений
- •Свойство 1. Оценки как мера дефицитности ресурсов
- •Свойство 2. Оценки как мера влияния ограничений на функционал
- •Свойство 3. Оценки - инструмент определения эффективности отдельных вариантов (технологических способов) с позиций общего оптимума
- •Тема 7. Транспортная задача линейного программирования
- •7.1. Постановка транспортной задачи
- •Классическая постановка транспортной задачи
- •Модели транспортной задачи
- •7.2.Методы построения исходного плана
- •Метод северо-западного угла
- •Метод минимального элемента
- •7.3.Оптимизация исходного базисного плана перевозок. Метод потенциалов
- •Основные процедуры метода потенциалов
- •Алгоритм метода потенциалов
- •7.4. Пример решения транспортной задачи
- •7.5. Применение модели транспортной задачи при решении различных экономических задач
- •Тема 8. Модели и методы дискретного программирования
- •8.1. Постановка задачи дискретного программирования
- •Задача о назначении (проблема выбора, задача о женихах и невестах)
- •8.2.Краткая классификация математических моделей дискретного программирования
- •8.3.Методы решения задач дискретного программирования
- •8.3.1. Методы отсечения для решения полностью целочисленной задачи линейного программирования
- •8.3.2.Сущность метода ветвей и границ
- •Тема 9. Модели и методы динамического программирования
- •9.1. Моделирование процессов наилучшего распределения ресурсов методом динамического программирования
- •Итоговая таблица условно-оптимальных решений
- •Графики предельной и средней эффективности
- •Тема 10. О других моделях и методах математического программирования
- •10.1.Нелинейное программирование
- •10.2.Стохастическое программирование
- •Тема 11. Модели конфликтных ситуаций в теории игр
- •11.1.Основные понятия теории игр
- •11.2.Решение игры в чистых стратегиях
- •11.3.Решение игры без седловой точки
- •Графический способ решения матричной игры
- •11.4. Пример решения экономической задачи методами теории игр
- •Тема 12. Модели управления запасами
- •12.1. Основные понятия
- •12.2. Статические модели управления запасами Уилсона
- •12.2.1. Статическая модель без дефицита
- •12.2.2. Статическая модель с дефицитом
- •12.3. Модели со случайным спросом
- •Тема 13. Модели массового обслуживания
- •Литература
5.5. Примеры решения задач линейного программирования графическим методом
Пример 1. Решим графическим методом задачу об использовании ресурсов (1), рассмотренную в §5.2. Модель этой задачи имеет вид:
|
f=12x1+15x2 max
x10, x20. |
|
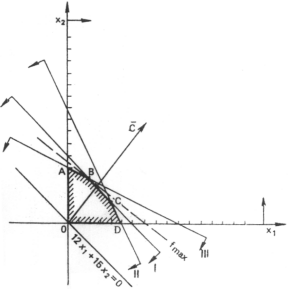
Рис. 4.
Рис. 4 показывает, что областью допустимых решений задачи является замкнутый ограниченный многоугольник ОАВСД и целевая функция достигает максимального значения в точке В. Точка В лежит на пересечении прямых:
|
|
(13) |
Для определения
координат точки В необходимо решить
систему (13) одним из следующих методов
(здесь удобнее пользоваться методом
Крамера). В результате получим, что
![]() ,
,
![]() ,
а fmax=122+154=84.
,
а fmax=122+154=84.
На основании полученного решения делаем вывод, что продукции вида Р1 следует выпускать 2 ед., продукции вида Р2 - 4 ед. При этом будет получен максимальный доход от ее реализации, который составит 84 ед. стоимости.
Пример 2. Решить графическим методом следующую задачу линейного программирования:
|
f=x1+x2 min
x10, x20. |
|
Областью допустимых решений данной задачи является замкнутый неограниченный многоугольник А'АВСС' (рис. 5).
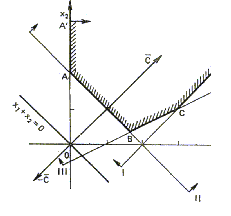
Рис. 5.
Поскольку прямая
f=x1+x2
=0 (целевая функция) и одна из граничных
прямых области определения x1+x2
=2 (рис. 5, прямая II) имеют
одинаковые угловые коэффициенты, при
параллельном перемещении прямой f=0
по области определения в направлении
вектора (-![]() )
она совпадает с указанной выше граничной
прямой.
)
она совпадает с указанной выше граничной
прямой.
Решением данной
задачи будет любая точка отрезка АВ.
Определим координаты граничных точек
отрезка АВ. Точка А имеет координаты
![]() ,
,
![]() .
Точка В лежит на пересечении прямых:
.
Точка В лежит на пересечении прямых:
|
|
(14) |
Следовательно,
целевая функция f
принимает минимальное значение в любой
точке отрезка, граничные точки которого
А(0, 2) и В![]() .
Задача имеет бесконечное число решений.
Для определения минимального значения
целевой функции необходимо подставить
координаты одной из точек отрезка, в
частности, точки А, в целевую функцию.
Тогда fmin=0+2=2.
.
Задача имеет бесконечное число решений.
Для определения минимального значения
целевой функции необходимо подставить
координаты одной из точек отрезка, в
частности, точки А, в целевую функцию.
Тогда fmin=0+2=2.
Пример 3. Рассмотрим задачу линейного программирования, которая не имеет оптимальных решений:
|
f=2x1+3x2 max
x10, x20. |
|
Областью допустимых решений данной задачи является замкнутый неограниченный многоугольник А'АВСС' (рис. 6).
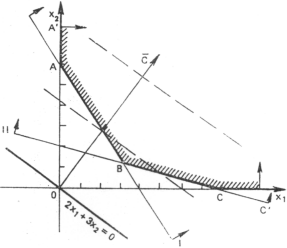
Рис. 6.
Передвигая прямую
f=2x1+3x2=0
параллельно самой себе по области
определения в направлении вектора
![]() (направление возрастания значений
целевой функции), убеждаемся в том, что
чем дальше эта прямая уходит от начала
координат, тем большее значение принимает
целевая функция.
(направление возрастания значений
целевой функции), убеждаемся в том, что
чем дальше эта прямая уходит от начала
координат, тем большее значение принимает
целевая функция.
Остановившись на одной из таких прямых, всегда можно найти допустимые точки, которые приносят большее значение целевой функции и лежат на других линиях уровня. Это обстоятельство дает возможность сделать вывод, что f . Данная задача решения не имеет, так как целевая функция не ограничена на множестве планов задачи.
Следовательно, в случае неограниченности множества допустимых решений задача линейного программирования может не иметь оптимальных решений.
Пример 4. Рассмотрим задачу линейного программирования, у которой отсутствуют допустимые решения:
|
f=2x1+x2 min
x10, x20. |
|
Рис. 7. показывает, что область определения данной задачи отсутствует, т.е. не существует точек, которые удовлетворяют одновременно всем ограничениям. Ограничения задачи несовместные. Задача решения не имеет, так как множество ее допустимых планов пусто.

Рис. 7.