
- •Спеціальна методика викладання математики
- •1. Методика розв'язування арифметичних задач
- •1.1. Задачі та їхня роль у навчанні і вихованні учнів допоміжної школи
- •1.2. Типи простих задач та їхня мета
- •Задачі на додавання
- •Задачі на віднімання
- •Задачі на множення
- •Задачі на ділення
- •1.3. Труднощі розв'язування арифметичних задач учнями допоміжної школи та помилки, які вони при цьому допускають
- •1.4. Організація роботи учнів над розв'язуванням арифметичних задач
- •1.5. Навчання учнів самостійному складанню задач
- •1.6. Перехід від розв'язування простих задач до складених
- •Порівняльний аналіз арифметичних задач
- •2. Усна лічба на уроках математики в допоміжній школі
- •2.1. Значення усної лічби для учнів допоміжної школи
- •2.2. Форми і прийоми усної лічби
- •2.3. Види вправ з усної лічби
- •5 Зупинок
- •2.4. Організація занять усною лічбою
- •3. Методика вивчення 1-го десятка
- •3.1. Причини виділення першого десятка в окремий концентр
- •3.2. Нумерація чисел в межах 1-го десятка
- •1. Знайомство з числом, кількістю і цифрою.
- •2. Визначення місця числа є числовому ряді.
- •3. Рахунок.
- •4. Порівняння чисел.
- •5. Склад числа.
- •3.3. Арифметичні дії з числами 1-го десятка
- •1. Знаходження суми або різниці шляхом перелічування.
- •3. Виконання арифметичних дій на основі знання складу чисел та складання таблиць додавання та віднімання у допоміжній школі.
- •4. Ознайомлення з переставною властивістю додавання.
- •5. Додавання і віднімання нуля і обчислення прикладів з відсутнім компонентом.
- •3.4. Розв'язування арифметичних задач в межах 10-ти учнями допоміжної школи1
- •4. Методика вивчення нумерації і арифметичних дій в межах 2-го десятка
- •4.1. Причини виділення другого десятка в окремий концентр
- •4.2. Вивчення нумерації чисел в межах 20-ти
- •Дев’ять на десять дев'ятнадцять
- •4.4. Розв'язування арифметичних задач у 2-му класі
- •5. Методика вивчення сотні у допоміжній школі
- •5.1. Причини виділення сотні в окремий концентр
- •5.2. Труднощі, які виникають в учнів допоміжної школи при вивченні сотні, та наочні посібники, які при цьому використовуються
- •5.3. Вивчення нумерації чисел в межах 100
- •1) Нумерація круглих десятків.
- •2) Вивчення нумерації круглих десятків.
- •3) Вивчення нумерації чисел 21-99.
- •5.4. Вивчення дій додавання і віднімання у межах 100
- •1. Додавання і віднімання без переходу через розряд.
- •2. Додавання і віднімання з переходом через розряд.
- •6. Методика вивчення множення і ділення
- •6.1. Формування в учнів поняття про множення і ділення
- •6.2. Навчання табличного множення і ділення в межах 100
- •6.3. Позатабличні випадки множення і ділення
- •6.4. Розв'язування задач у 3-4-му класах
- •7. Методика вивчення тисячі
- •7.2. Усна і письмова нумерація чисел в межах 1000
- •7.2.1. Знайомство з сотнею як новою лічильною одиницею та нумерація круглих сотень.
- •7.2.2. Утворення повних трицифрових чисел та їх запис.
- •7.2.3. Утворення неповних трицифрових чисел і їх запис.
- •7.3. Обчислення прикладів на додавання і віднімання в межах тисячі
- •1. Додавання і віднімання без переходу через розряд.
- •2. Додавання і віднімання з переходом через розряд.
- •8. Вивчення метричної системи мір
- •8.1. Метрична система мір та основні труднощі її засвоєння розумово відсталими школярами
- •8.1.1. Знайомство з мірами довжини.
- •8.1.2. Вивчення мір об'єму.
- •9.1.3. Вивчення мір маси.
- •8.1.4. Вивчення мір вартості.
- •8.2. Перетворення чисел, які виражаються метричними мірами
- •2. Додавання і віднімання іменованих чисел з перетворенням.
- •9. Методика вивчення мір часу
- •9.1. Час та особливості його вивчення учнями допоміжної школи
- •9.2. Перетворення чисел, виражених мірами часу і арифметичні дії з ними
3) Вивчення нумерації чисел 21-99.
Після вивчення круглих десятків вчитель показує учням утворення будь-якого повного двоцифрового числа. Для цього потрібно показати загальний принцип утворення цих чисел.
Вивчення нумерації чисел від 21 до 100 починається з повторення утворення і назв розрядних чисел другого розряду (10, 20, 30 ... 100), а потім уже організовується утворення будь-яких двоцифрових чисел. Як основний тип наочності при їх утворенні використовуються пучечки (десятки) і окремі палички. Порядок розташування чисел натурального ряду варто проілюструвати за допомогою квадрату "сотня", клітинки якого заповнюються учнями самостійно.
Для пояснення нумерації чисел від 21 до 100 використовується бесіда, мета якої – повідомити учням, що оскільки вони вже навчились рахувати і записувати числа до 20, то тепер так само зможуть вивчити назви й інших чисел, які йдуть після 20, тому що числовий ряд на цьому не закінчується.
На набірному полотні вчитель виставляє, або бере в руку 2 пучечки - 2 десятки паличок, тобто число 20 і до нього додає ще 1 паличку. "Скільки в нас було паличок?" (2 десятки або 20). "А тепер я до них додаю ще одну паличку. Отже, у нас буде два десятки паличок і ще одна паличка. Ми дістали нове число, на 1 більше, аніж число 20. Це число також має свою назву. Що ми зробили?" (До 20 додали 1 паличку). "Таким чином, двадцять і одна паличка утворює нове число, яке називається двадцять одне. Давайте повторимо його і розглянемо на рисунку, як воно утворюється". Після цього діти розглядають малюнок, а на набірному полотні відтворюють міркування педагога.

Після цього діти працюють самостійно. "Тепер у себе на партах відкладіть 2 пучечки - 2 десятки паличок і ще 1 паличку. Яке число отримали? Скільки в ньому десятків, скільки одиниць?" Утворення нових чисел продовжується. "До 21 додамо ще одну паличку, буде 2 десятки паличок і 2 палички, або 22 палички. Це число містить у собі 2 десятки і 2 палички і називається двадцять два.

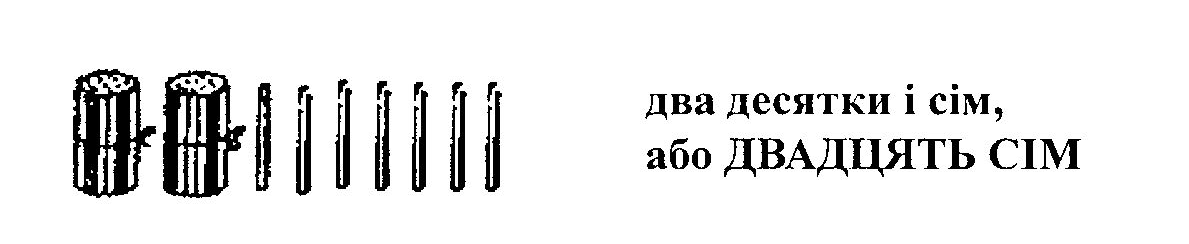
Вчитель продовжує: "Поставимо на набірне полотно до 2 десятків і 8 паличок ще 1 паличку. Скільки всього паличок стало? (Двадцять дев'ять). А тепер до 29 додамо ще 1 паличку, буде 2 десятки і ще 10 паличок, або 2 десятки і ще 1 десяток. Отже, всього буде З десятка, або тридцять.
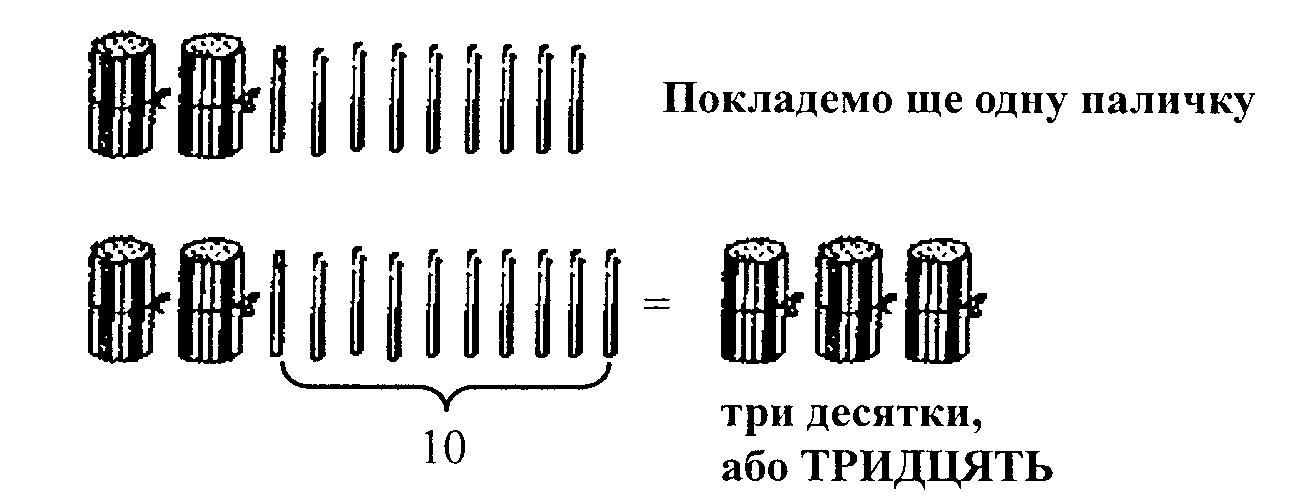
Після утворення числа 30 учитель просить учнів назвати усі числа від 20 – 30. Так само проводиться ознайомлення з числами від 31 – 40 і далі до 100.
Кожному учневі треба дати можливість порахувати по одному від 1-100 і навпаки як з використанням наочності, так і абстрактно. Особлива увага звертається на рахунок від заданого числа до заданого
3 переходом через розряд.
Для закріплення знань про нумерацію чисел в межах 100 можна запропонувати такі завдання:
назвати число на 1 менше (більше) даного;
які сусідні десятки числа, наприклад ... 40 ...;
виконати аналіз числа за його десятковим складом: 49 – це 4 десятки і 9 одиниць;
назвати всі числа третього десятка (четвертого, п'ятого тощо);
назвати всі двоцифрові числа, у яких число одиниць п'ять;
покласти 3 десятки паличок і ще 3 палички. Скільки паличок всього стало? Як дістати наступне число?
відкласти на рахівниці, абаці число 25, 44. Скільки в них десятків, скільки одиниць?
показати на лінійці 3 дм і 5 см. Скільки всього сантиметрів?
накреслити відрізок довжиною 2 дм і 4 см. Скільки це сантиметрів?
10) заповнити таблицю "сотня".
Вивчення нумерації можна починати і зі складання чисел за допомогою числових табличок з наклеєними на них різнокольоровими цифрами. Це потрібно робити для того, щоб уникнути помилок, які роблять розумово відсталі учні, коли зразу записують двоцифрові числа у зошиті. Наприклад, число 36 вони записують як 306 (тридцять і шість). Якщо не виправити помилки в цей період, то в наступному учні будуть не помічати помилок при записі чисел сто вісім (1008), сто тридцять шість (100306). Лише чітке усвідомлення того, що пишемо ми числа дещо по-іншому, аніж промовляємо і чуємо, дозволить уникнути таких помилок і, як наслідок, неправильних результатів обчислень.
Переваги використання даного прийому полягають у тому, що:
ми даємо учням цифрові таблички, серед яких немає нуля і тому уникаємо помилкового його застосування;
таблички легко можна поміняти місцями і тим самим показати залежність зміни величини числа від зміни місця цифр, які позначають дане число;
кожен учень може безпосередньо маніпулювати цими табличками;
вчителю легше контролювати діяльність школярів за рахунок використання різних кольорів для позначення десятків і одиниць.
Л. Єлєньска пропонує знайомство з нумерацією чисел в межах сотні проводити в три етапи.
На першому етапі потрібно пов'язати запис двоцифрового числа з конкретним образним уявленням цього числа. Для цього у спеціальній школі доцільно використати набір паличок, зв'язаних в пучки і розкладених по одиниці, арифметичну шухляду з брусками, що вказують десятки, і кубиками, що вказують одиниці.
Наприклад,
взяли 2 десятки паличок і ще 1 паличку і
отримали число
21. Роздаємо школярам два комплекти цифр
від 1 до 9 різного  кольору
- червоного, який позначає десятки, і
синього – який позначає одиниці.
Вчитель проводить пояснення: "Подивіться,
скільки паличок ми взяли. Знайдіть серед
набору синіх цифр ту, яка вказує на
кількість паличок
(знайдену цифру школярі кладуть під 1
паличкою). Подивіться,
скільки пучків ми взяли? Знайдіть серед
червоних цифр ту, яка вказує на кількість
пучків. Покладіть її під пучками паличок
(учні
кладуть 2 під пучками). Скільки десятків
є у даному числі? Скільки одиниць є у
ньому? (ці запитання краще підкреслюють
поняття
про розсипані палички, які позначають
одиниці, і про зв'язані, що
позначають десятки). Ми утворили нове
число - двадцять один". Вчитель
пояснює, що числівники утворюються з
двох слів. Спочатку вимовляються
десятки, а потім одиниці. Це число
відкладається на рахівницях. Так з
десятків і одиниць на конкретному
рахунковому матеріалі
учні повинні навчитися утворювати
будь-яке двоцифрове число
і називати його.
кольору
- червоного, який позначає десятки, і
синього – який позначає одиниці.
Вчитель проводить пояснення: "Подивіться,
скільки паличок ми взяли. Знайдіть серед
набору синіх цифр ту, яка вказує на
кількість паличок
(знайдену цифру школярі кладуть під 1
паличкою). Подивіться,
скільки пучків ми взяли? Знайдіть серед
червоних цифр ту, яка вказує на кількість
пучків. Покладіть її під пучками паличок
(учні
кладуть 2 під пучками). Скільки десятків
є у даному числі? Скільки одиниць є у
ньому? (ці запитання краще підкреслюють
поняття
про розсипані палички, які позначають
одиниці, і про зв'язані, що
позначають десятки). Ми утворили нове
число - двадцять один". Вчитель
пояснює, що числівники утворюються з
двох слів. Спочатку вимовляються
десятки, а потім одиниці. Це число
відкладається на рахівницях. Так з
десятків і одиниць на конкретному
рахунковому матеріалі
учні повинні навчитися утворювати
будь-яке двоцифрове число
і називати його.
На другому етапі школярів потрібно підвести до усвідомлення значення місця цифри у числі. Для цього вчитель дає завдання: скласти число 23 з розрізнених паличок і паличок, зв'язаних у пучки. Підставляємо під пучки цифру 2, а під розрізнені палички - 3. Називаємо це число зліва направо - двадцять три. Потім пропонуємо забрати 1 паличку і добавити 1 пучок. Підставляємо знову під пучки і палички цифри відповідного кольору, наприклад, 3 і 2. Яке число утворилось? Називаємо його - тридцять два. Отже, цифри залишились ті ж, а число змінилось. Ставимо запитання "Яка цифра тепер позначає десятки, а яка одиниці?"
У процесі виконання таких завдань вчитель звертає увагу школярів на місце, на якому лежить цифра, що позначає десятки, і цифра, що позначає одиниці. Кращому закріпленню залежності між величиною числа і місцем цифри, яка позначає дане число, сприяє перехід до запису чисел під диктовку на дошці з відповідним коментуванням.
Особливу увагу потрібно звернути на запис чисел, які позначаються двома однаковими цифрами: 22, 33, 44 і т.д. Вчитель повинен показати, що за числом 21 іде наступне число - 22, що випливає з закономірностей утворення числового ряду. При позначенні цього числа використовуємо дві однакові цифри (в даному випадку двійки).Але перша справа двійка вказує на кількість у ньому одиниць, а друга - десятків. Тому це число читається як двадцять два. Завдання, які виконуються школярами самостійно, викликають у них цікавість і мають значне освітнє значення.
Лише після того, як учні навчаться складати на таблицях будь-яке двоцифрове число, читати і записувати його, відкладати на рахівницях, на набірному полотні і виконувати з ним інші дії, можна переходити до вивчення числового ряду від 1 до 100.
На третьому етапі Л. Єлєньска пропонує знайомити школярів з 0 як арифметичним знаком, що позначає відсутність одиниць певного розряду. Лише після того, як школярі зрозуміють, що цифра, яка стоїть у числі на першому місці справа позначає одиниці, а цифра, яка стоїть на другому - десятки, можна переходити до усвідомлення значення нуля.
Нуль - це геніальний винахід. Введення нуля для позначення пустого розряду дозволило десяткову систему числення визначити найбільш ефективною для обчислення і відкинути абак. Але потрібно вказати, що 0 як арифметичний знак, що позначає відсутність одиниць в якомусь розряді, був винайдений лише в IV столітті нашої ери в Індії. З Індії він перейшов до арабів, потім в Іспанію в X столітті, а далі в Італію та Францію. На територію України нуль потрапив лише на початку XIV століття.
Для того, щоб усвідомити значення 0, потрібно відчути нагальну необхідність у ньому. Для цього Л. Єлєньска використовує лабораторно-практичний метод: "Позначте цифрами число 21 (для цього учні повинні використовувати лише цифрові кольорові таблички). Відкинемо 1. Яке число залишилось? Що позначає цифра 2?" Вчитель підкреслює значення місця у цифри: "Яку цифру ми можемо покласти біля 2, щоб позначити число двадцять?" Потрібно зазначити, що хоч школярі вже знайомі з числом 20 і писали його на задане запитання вони знаходять відповідь не відразу. Це є свідченням неусвідомленого розуміння арифметичного знака 0. Після того, як школярі попробують декілька варіантів утворення числа двадцять за допомогою таблиць, їм пояснюється, що у цьому випадку у розряд одиниці ставиться арифметичний знак 0, який позначає їх відсутність у даному розряді.
 Під
час вивчення 0 від школярів вимагається
пояснення його використання:
"Покладіть на парту цифру 3. Як зробити,
щоб вона позначала
3 десятки? Для чого ми поклали правіше
0? Яке число утворилось?"1
Під
час вивчення 0 від школярів вимагається
пояснення його використання:
"Покладіть на парту цифру 3. Як зробити,
щоб вона позначала
3 десятки? Для чого ми поклали правіше
0? Яке число утворилось?"1
Після засвоєння загального принципу утворення і запису двоцифрових чисел, переходять до роботи над утворенням і записом чисел 21-99 та закріпленням знань послідовності чисел від 1 до 100.
Під час роботи з розумово відсталими учнями по вивченню нумерації постійно звертається увага на утворення кожного нового десятка, проводячи розгорнутий аналіз і використовуючи для цього наочні посібники:
29 + 1 = 2 дес. 9 од. + 1 од. = 2 дес. 10 од. = 3 дес.
30 – 1 = 3 дес. – 1 од. = 2 дес. 10 од. – 1 од. = 2 дес. 9 од. = 29
99 + 1 = 9 дес. 9 од. + 1 од. = 9 дес. 10 од. = 10 дес. = 100
100 – 1 = 10 дес. – 1 од. = 9 дес. 10 од. – 1 од. = 9 дес. 9 од. = 99.
Кожній дитині варто запропонувати порахувати по одному від 1 до 100 і назад, оперуючи різними посібниками і без них.
Для фронтальної роботи в класі вчитель виготовляє таблицю чисел від 1 до 100, які можна вписати у сто клітинок квадрата 10x10 ("сотня"). Спочатку учні читають числа, потім розбираються в структурі таблиці з допомогою вчителя. Вони приходять до висновку, що кожен ряд - це десяток, останній стовпчик - це круглі десятки, всього 100 чисел, в кожному ряді кількість десятків змінюється в останньому числі і т.д. (див. рис. 5.1., стор. 181).
Вони повинні накреслити таку таблицю в себе в зошиті, вміти заповнювати квадрати числами у прямому і зворотному порядку, вписувати парні, непарні числа, групові числа тощо. За допомогою таблиці можна порівнювати числа, які стоять поруч у ряді (на скільки одиниць одне число більше або менше за сусіднє); усі числа одного ряду (число десятків однакове, крім останнього числа, а число одиниць змінюється); числа між собою в стовпчиках (число десятків змінюється, а число одиниць - ні). Кожне число в стовпчик}? можна порівняти з тими, які знаходяться вище і нижче нього.
Всі випадки утворення наступного десятка потрібно виписати і розібрати:
29 + 1 = 30 – отримуємо новий десяток.
39 + 1 = 40 – отримуємо новий десяток.
99 + 1 = 100 – отримуємо сотню.
Так само розглядаються і випадки віднімання:
60 – 1 =... – розбиваємо один десяток на одиниці і віднімаємо 1, залишається 5 десятків 9 одиниць. Отже, 60 – 1 = 59.
Всі ці дії виконуються під керівництвом вчителя і ілюструються за допомогою наочного матеріалу (паличок, рахівниці, таблиць, абаку тощо).
Особлива увага звертається на рахунок від заданого до заданого числа з переходом через десяток у прямому і зворотному напрямку. Так само, як і при вивченні чисел 1-го і 2-го десятка, необхідно закріпити зі школярами властивості натурального ряду чисел: кожне число більше попереднього і менше наступного на одиницю.
При вивченні нумерації в межах 100 учні знайомляться з розрядною таблицею (див табл. 5.3.). Вчитель вводить новий термін "розряд", повідомляючи, що одиниці відносяться до першого розряду і пишуться в числі на першому місці праворуч, десятки - до другого розряду і пишуться в числі на другому місці праворуч, а сотні - до третього розряду і пишуться в числі на третьому місці праворуч: 3-й розряд - сотні; 2-й розряд - десятки; 1-й розряд-одиниці. Для пояснення цього матеріалу можна використати абак, в якому всі цифри мають різний колір і вказують на різні розрядні одиниці.
Таблиця 5.3.
|
сотні |
десятки |
одиниці |
|
|
|
|
Починаючи з 3-го класу, вчитель формує у школярів вміння порівнювати числа між собою, використовуючи таблиці розрядів. При цьому він зазначає, що порівняння починається з вищих розрядів (якщо число десятків більше, то на одиниці можна і не дивитись, тому що все число буде більше: 45 < 54, адже 4 дес. < 5 дес.). При порівнянні чисел за допомогою таблиць доцільно дотримуватись такої послідовності:
 Таблиця
5.4.
Таблиця
5.4.
|
десятки |
одиниці |
|
7 |
2 |
|
9 |
2 |
Таблиця 5.5.
|
десятки |
одиниці |
|
2 |
6 |
|
6 |
2 |
Таблиця 5.6.
|
десятки |
одиниці |
|
2 |
1 |
|
1 |
1 |
Таблиця 5.7.
|
десятки |
одиниці |
|
2 |
8 |
|
3 |
1 |
Окремо вивчаються випадки порівняння чисел 1 і 10, 1 і 100, 10 і 100, 1 і 20, 2 і 20, 30 і 10 і т.д. Тренуючись у порівнянні чисел, школярі поступово навчаться не лише правильно виділяти більше або менше з них, але й пояснювати свій вибір.
Учні мають навчитися змінювати розряди в числі. Використовуючи набірне полотно, рахівницю, вчитель дає завдання скласти число, а потім провести в ньому певні зміни (збільшити, зменшити).
У школярів потрібно сформувати вміння записувати одне і те ж число трьома різними способами: 36; 30 + 6; З дес. 6 од.
На всіх уроках бажано використовувати рахівниці. Потрібно навчити учнів рахувати на них у прямому і зворотному напрямку, групами, складати числа, вносити зміни в числа тощо. Особливу увагу приділяють лічбі на рахівницях у прямому і зворотному напрямку, що надалі стане основою для вивчення додавання і віднімання.
Для закріплення нумерації учням даються приклади на виконання дій додавання і віднімання, прийоми обчислень яких опираються на знання властивостей натурального ряду чисел (24 + 1 =, 25 – 1 =), а також на знання десяткового складу чисел (40 + 8 =, 48 – 8 =, 48 – 40 =). Тут можна використати цікаві квадрати, у яких сума або різниця повинні співпадати по вертикалі і горизонталі.
Для обчислення прикладів типу 24 + 1 = і 25 – 1 = наочним посібником виступає таблиця з записом чисел від 1 до 100 (щоб довідатися результат додавання до числа одиниці, потрібно в числовому ряді знайти наступне за ним число, а щоб взнати результат віднімання від числа одиниці - попереднє число). Спочатку при додаванні і відніманні чисел з одиницею учні опираються на знання властивостей числового ряду. Потім цим посібником дозволяється користуватися лише тим школярам, які ще недостатньо вивчили послідовність чисел.
На вивчення нумерації виділяється не менше 5-й уроків, завдання яких повністю передбачають знайомство з властивостями чисел в межах 100. На першому уроці учні знайомляться з утворенням та записом круглих десятків; на другому - утворення і запис чисел першої сотні; на третьому – пряма і зворотна лічба по одному в межах 100; на четвертому – число і цифра; помісне значення цифри у числі; порівняння чисел; на п'ятому – повторення нумерації чисел в межах 100.
Під час вивчення нумерації урок може мати таку структуру:
повторення прямого і зворотного рахунку від 1 до 10;
повторення прямого і зворотного рахунку від 10 до 100 (+10; – 10);
повторення назв розрядів і робота з розрядною сіткою. Запис чисел у таблицю під диктовку. Читання чисел, записаних у таблицю і т.д.;
робота з паличками, з арифметичною шухлядою;
складання чисел з допомогою карток, запис результатів чисел 15 – 1 дес. 5 од., 15 = 10 + 5;
робота з рахівницею. Місце одиниць і десятків на рахівниці. Складання чисел, зміна чисел. Запис чисел у зошитах

 порівняння
чисел типу: 26 8; 39 27; 5 54;
8
88; 2 92 і т.д.
порівняння
чисел типу: 26 8; 39 27; 5 54;
8
88; 2 92 і т.д.запис чисел в зошит стовпчиком з дотриманням правила позначення розрядів1.
Але це не значить, що на наступних уроках цьому питанню не потрібно приділяти уваги. На кожному уроці у час, відведений для усного рахунку, педагог проводить повторення і закріплення знань нумерації". При включенні в план наступних уроків вправ на нумерацію вчителю необхідно слідкувати за тим, щоб вони не суперечили темі, були логічно пов'язані з матеріалом, давались у певній послідовності, відповідали індивідуальним особливостям школярів тощо.
