2.2. Форми і прийоми усної лічби

Форми усних обчислень різноманітні, але всі їх можна розді­лити на три основні групи - слухові, зорові та зорово-слухові.

При застосуванні першого типу учням пропонуються вправи в чисто слуховій формі. Школярі здійснюють обчислення або з запи­сом, який йде слідом за усним розв'язуванням, або без нього. Вихован­ці сприймають завдання, опираючись лише на слуховий аналізатор. Така форма усної лічби використовується, коли треба відпрацювати навички швидкої лічби.

У другому випадку школярам пропонується виконати вправи у зоровій формі. Вчитель записує арифметичні приклади або задачі на таблицях, картках, на класній дошці тощо. Зорове сприймання чисел звільняє учнів від необхідності утримувати їх у пам'яті до тих пір, поки розв'язання буде виконане. Цей тип усної лічби використову­ється на всіх роках шкільного навчання, але перевага надається все-таки у молодших класах.

Третій тип вправ можна пропонувати для обчислення шко­лярам у зорово-слуховій формі. Учні сприймають завдання не тільки на слух, але й з використанням наочних посібників. При цьому вони можуть відповідати як усно, так і з записом у зошиті та на дошці.

Усні обчислення проводяться при наявності класних та індивідуальних таблиць, записів на дошці, з використанням індивіду­альних карток. Числа і арифметичні дії вказані у цих записах і такимчином звільняють школярів від необхідності виконувати їх запис у зошитах. Наведемо приклади завдань, які рекомендуються для вико­ристання в допоміжній школі¹.

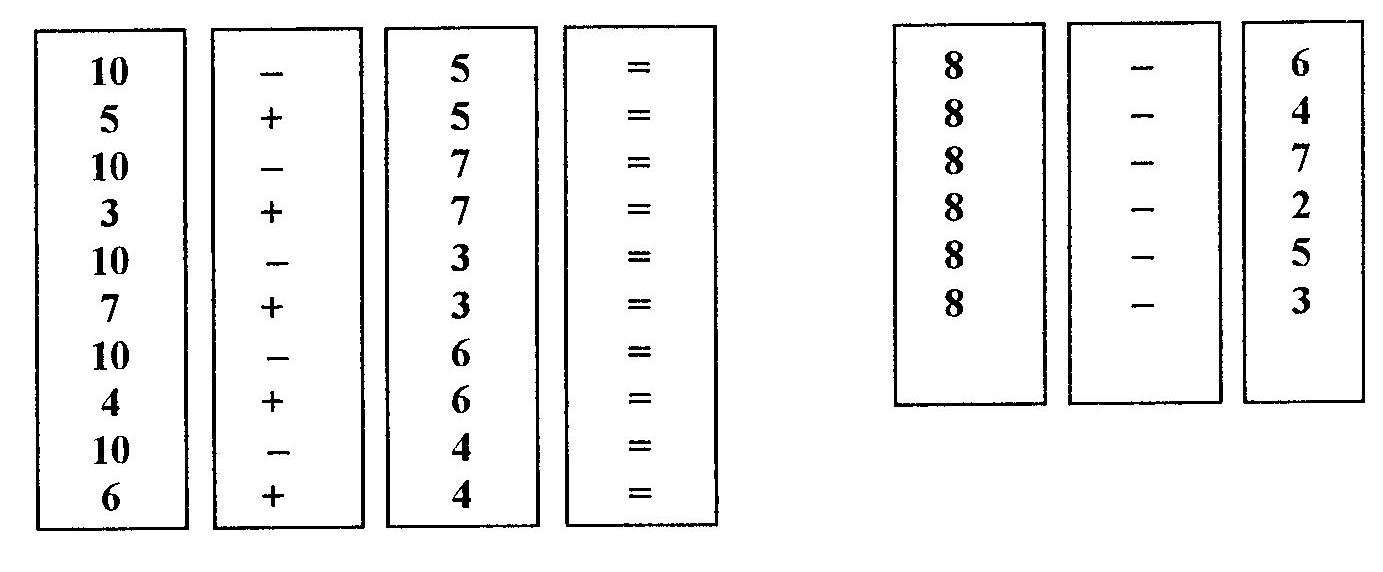
1. Вчитель вивішує перед учнями з набору лічильних стрічок дві стрічки з числами і проміжну стрічну з вказаними на ній арифме­тичними знаками дій, та пропонує їм виконати обчислення:

2. На дошці вчитель креслить квадрат або коло для гри в мовчанку і розставляє в ньому декілька квадратиків з прикладами, які школярі мають обчислити усно.

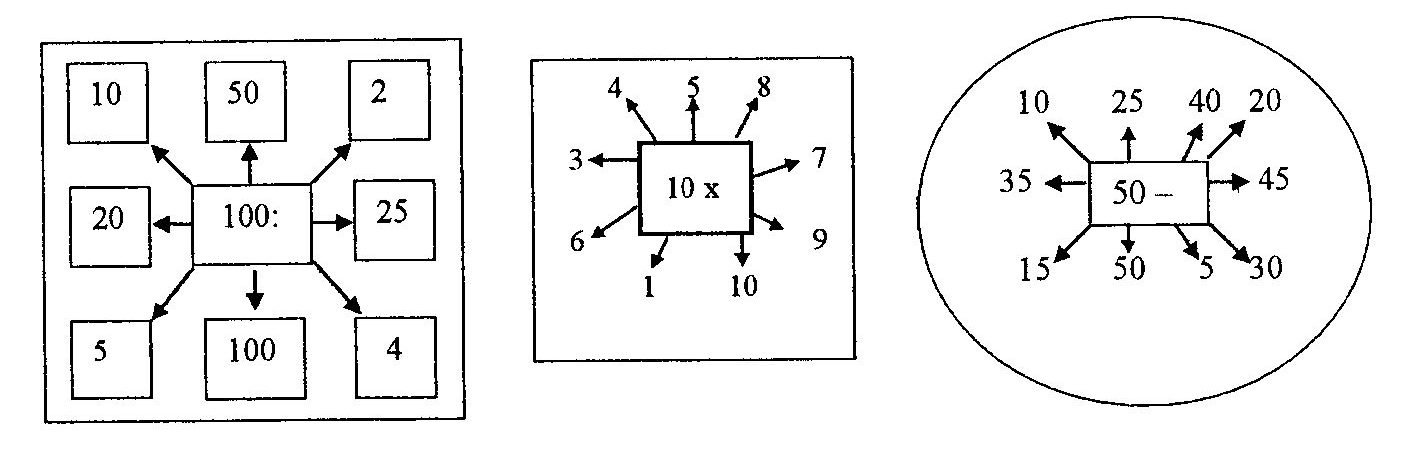
3. Перед початком вправ в усному рахунку кожен з учнів отри­мує табличку з прикладами "кругові приклади". Вчитель пропонує уважно їх розглянути, обдумати відповідь, тобто попередньо самостійно виконати обчислення і підготуватись до відповіді. А оскільки всі таблички різні, то інші учні повинні уважно слухати відповіді товаришів і у випадку необхідності коригувати або доповнювати їх.

На перших етапах роботи школярам дозволяється користуватись табличками з цифрової каси. Для окремих школярів, які відчувають значні труднощі в запам'ятовуванні чисел, цифрові таблички можуть залишатись і на триваліший час. Коли діти оволодівають принципом побудови "кругового прикладу", їм пропонується виконувати обчис­лення усно, попередньо прочитуючи кожен рядок вголос.

Зразки табличок з "круговими прикладами"

1-й клас: 6 + 4 =  – 5 =  + 3 =  – 2 = 6

4-й клас: 100 : 4 = ?

? х 3 = ?

? – 25 = ?

? х 2 = ?

? : 5 = ?

? х 4 = ?

? – 30 = ?

? + 40 = ?

? – 60 = ?

? + 70 = 100

Вчитель може підготувати картки з "круговими прикладами" на цупкому папері різного кольору для занять на уроках і для домаш­ніх завдань. Кожен з наборів "серії" прикладів виконується на папері одного кольору. Це дає можливість швидко привести до порядку всю картотеку після роботи з нею на уроці, а головне - полегшує вчителю можливості роздачі карток-завдань учням з урахуванням їхніх індивідуальних можливостей. Картки "кругових прикладів" можуть бути виконані учнями і для особистого користування в домашніх умовах і під час ігор.

4. Набори лічильних стовпчиків і стрічок також є цікавим посібником для використання на заняттях усним рахунком. Наведемо приклади лічильних стовпчиків.

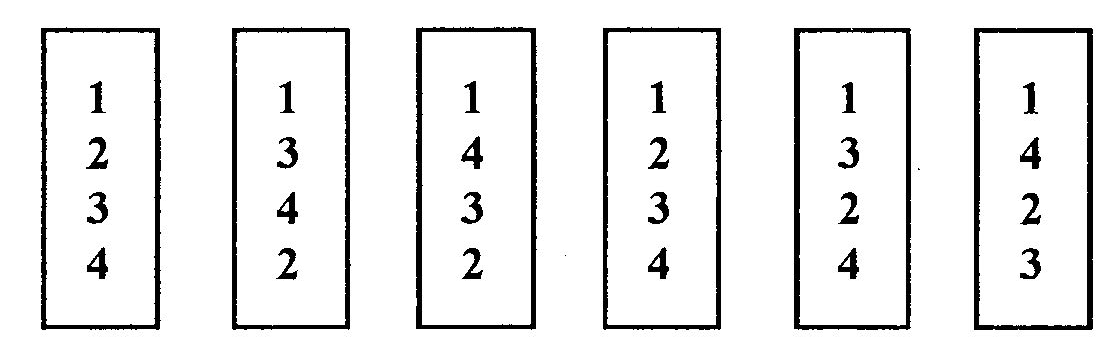
Кожен з учнів отримує стовпчик з цифрами (в даних випад­ках - перший) і по ньому виконує обчислення на додавання, послідов­но додаючи одне число до іншого:

1 + 2 = 3 3 + 3 = 6 6 + 4 = 10

Наступний раз кожен учень отримує один або два стовпчики з цифрами і самостійно складає приклади.

Вправа може бути змінена: вчитель пише на класній дошці число 10 і пропонує школярам відняти всі числа, написані на стовп­чику:

10 – 1 = 9 9 – 2 =7 7 – 3 = 4 4 – 4 = 0

На одному з занять школярам пропонується додати три пер­ших числа і від їхньої суми відняти останнє:

1+2+3=6 6 – 4=2

Можна запропонувати додати два перших числа і два останніх і від більшої суми відняти меншу:

1 + 2 = 3 3+4=7 7 – 3 = 4

Рахункові стрічки

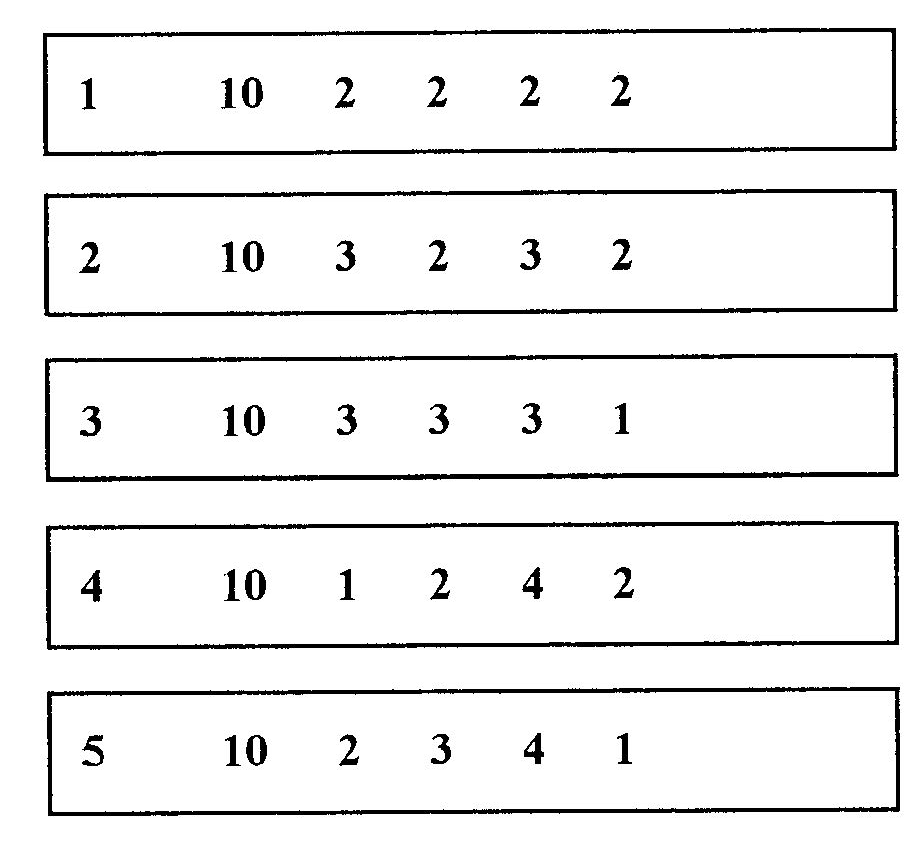
На уроках можна запропонувати школярам виконати такі завдання з лічильними стрічками:

• від 10 послідовно відняти число за числом;

• додати всі одноцифрові числа і отриману суму відняти від 10 і т.д.

Ці стрічки можуть бути виготовлені не лише у вигляді роздаткового матеріалу, але й у вигляді наочних посібників більшого розміру. При цьому вчитель може його розміщувати перед учнем, намічає той чи інший тип вправ, пояснює його школяру і, показуючи число за числом указкою, проводить заняття.

Вправи з усної лічби можуть супроводжуватись записом лише результатів обчислень або наступним записом кожного вирішеного прикладу:

1. Вчитель диктує приклади, використовуючи для цього серію табличок:

а) 75 + 25 – 50 б) 100 : 2 + 25 в) 25 x 4 – 75

60 + 40 – 80 100 : 4 + 50 30 x 3 – 40

35 + 45 – 30 100 – 60 + 25 15 x 6 – 25

48 + 32 – 60 100 – 80 + 50 10 x 6 – 15

Учні записують у зошит відповіді: а) 50; 20; 50; 20. б) 75; 75; 65; 70. в) 25; 50; 65; 45.

2. На дошці записуються приклади:

а) 250 x 2 – 325 б) 1000 : 2 – 250 в) 500 х 2 : 4

500 x 2 – 750 1000 : 2 + 250 500 x 2 : 10

350 x 2 – 350 1000 : 4 x 3 250 : 5 x 7

400 x 2 – 225 1000 : 5 x 4 250 : 5 x 10

Учні виконують обчислення і записують його результати, а потім під час самостійної роботи на уроці або при виконанні домаш­нього завдання їм пропонується скласти приклади на ту чи іншу арифметичну дію або на всі арифметичні дії, щоб в результаті були отримані тільки що записані числа.

3. Вчитель записує на дошці ряд чисел і пропонує учням скласти два-три складні приклади на одну арифметичну дію так, щоб в результаті було дане число. Приклади складаються усно, а потім записуються письмово:

а) додавання б) віднімання в) множення г) ділення

750 250 600 150

250 + 300 + 200 1000 – 500 – 250 100x2x3 900:3:2

400 + 200+150 750 – 150 – 350 25x4x6 900:2:3

105 + 245 + 400 1000 – 420 – 330 50x6x2 900:6:1

4. Вчитель записує на дошці число і пропонує кожному учню скласти по чотири приклади: по одному на кожну арифметичну дію так, щоб в результаті було отримане дане число. Складаються прик­лади усно, а потім записуються і зачитуються.

Запис вчителя

а) 75 б) 100 в) 250 г) 500

Роботи школярів а) б) в) г)

25 + 50 50 + 50 125 + 125 250 + 250

100–25 250–150 500–250 1000–500

25x3 25x4 50x5 125x4

150:2 500:5 1000:4 1000:2

Можна запропонувати учням скласти складні приклади на декілька арифметичних дій з заданою відповіддю. Багатоманітність варіантів в запропонованих учням прикладах розширює арифметичні уявлення школярів, створює цікавість до роботи, привчає до самостій­ності і сприяє міцності знань і виховання навичок усного рахунку.

5. Робота по формуванню навичок усного рахунку може про­водитись з використанням лічильних карток. При цьому перед школярами ставиться завдання заповнити пусті клітинки відповід­ними числами.

2
				20
3		9		15
	21		27
9			36
	63			90

Картки можуть даватись школярам (по одній кожному), і вони один за одним відповідають, "заповнюючи" пусті клітинки своєї картки. Також карти можуть бути накреслені на дошці, а викликаний учень заповнює пусті клітинки табличками з відповідними числами. Після заповнення картки можна запропонувати школярам виконати додаткові завдання, наприклад, записати стовпчики прикладів на додавання, віднімання тощо. Наприклад:

10+10 = 20; 20 + 10 = 30; 30+10 = 40.... 90 + 10=100

10x2 = 20; 10x3 = 30; 10x4 = 40.... 10x10=100

100–10 = 90; 90–10 = 80; 80–10 = 70 .... 20–10 = 10.

6. Робота з лічильними квадратами. Кожен учень отримує квадрат, який розділений на 9 клітинок (три ряди по три клітинки), або креслить такий квадрат у себе в зошиті. Вчитель креслить такий самий квадрат на дошці, далі в середній і кутових клітинках ставить числа і пропонує школярам у вільні клітинки поставити такі числа, щоб сума чисел в кожному рядку і в кожному стовпчику дорівнювала 15.

2		6		8		6		4		8		4		2
	5				5				5				5
4		8		4		2		2		6		8		6

7. Стрічка числового ряду. Під час роботи з нею школярам пропонується знайти суму всіх парних чисел, а потім всіх непарних і результати записати у вигляді прикладів.

1

2

3

4

5

6

7

8

9

10

Вправи в обчисленні арифметичних прикладів без поперед­нього або наступного запису чисел - це третя форма усних обчислень. Як і перші дві, вона необхідна на всіх роках навчання школярів. Ускладнення окремих вправ можливе завдяки ускладненню матеріалу, який вивчається.

На перший план у них виступають вправи в "швидкому рахун­ку". Особливу увагу до цього типу занять потрібно надавати у молодших класах, щоб рахунок у межах першої сотні був чітким і безумовно правильним до того часу, як учень почне вивчати багатоцифрові числа і дроби.

Для того, щоб уміння рахувати усно було сформоване усвідом­лено, необхідно систематично проводити обчислення прикладів у поєднанні з усним поясненням ("розповіддю") шляхів вирішення. Упроцесі використання усного пояснення шляхів вирішення прикла­ду або розв'язання задачі учень закріплює свої знання і вміння аналізу­вати число, розкривати його десятковий склад.

Серед учнів допоміжної школи зустрічаються діти, які важко виучуються виконувати аналіз чисел, розкривати їхній десятковий склад. Враховуючи це, необхідно полегшити їм засвоєння цього матеріалу. Можна запропонувати такий прийом. Наприклад, потрібно 250 помножити на 3. Для його обчислення викликаються два учні: одному пропонується розповісти шлях вирішення, а іншому - записа­ти це на дошці.

Враховуючи неоднорідність складу учнів класу, нерівномір­ність розвитку них математичних здібностей, наявністю різноманіт­них психофізичних порушень захоплюватись якоюсь однією формою усних вправ не можна. У допоміжній школі їх краще за все чергувати. Прийоми усних обчислень розділяють на загальні та прикладні. У своїй основі вони містять закономірності десяткового складу числа, а також законів та властивостей арифметичних дій. Знання загальних прийомів усного рахунку доступні більшості розу­мово відсталих школярів. Оволодівають цими прийомами вони в процесі систематичних вправ і тренувань. Із групи прикладних прийомів лише деякі доступні для усвідомленого використання учнями допоміжної школи.

До загальних прийомів усних обчислень відносяться прийоми додавання і віднімання по одинці, прийоми, в основі яких лежать знання складу чисел, на розкладанні одного з компонентів арифметич­ної дії на розрядні одиниці, на використанні прийому перестановки доданків, на розкладанні одного числа на рівні числа, з яких воно складається тощо. Вони загальновживані до всіх чисел. Наприклад, при виконанні прикладів на додавання або віднімання чисел в межах 100 необхідно розкласти другий компонент арифметичної дії на десятки та одиниці, а надалі послідовно їх об'єднати з першим доданком (при додаванні) або послідовно відняти зі зменшуваного (при відніманні):

24 + 15 = 39 38–25 = 13

15 = 10 + 5 25=20 + 5

24 + 10 = 34 38=20–18

34 + 5 = 39 18–5 = 13

Прикладними прийомами усних обчислень називаються прийоми, які застосовуються лише до окремих чисел. Засвоєння цих прийомів викликає значні труднощі у розумово відсталих школярів. Тому в програму для допоміжної школи включені лише деякі прийоми заокруглення доданків, множення на 10 і на 5, множення на 9, 11. Використання їх у допоміжній школі взагалі обмежене.

Знайомити учнів з прийомом округлення необхідно лише після того, як вони навчились користуватись загальними прийомами. Використання прикладних прийомів округлення викликає труднощі тому, що виконавши додавання однієї або декількох одиниць для округлення числа, вони забувають їх віднімати після виконання обчислення. Виконавши вказану дію, учень залишає свою роботу незавершеною. Тому лише окремі учні допоміжної школи можуть оволодіти цими прийомами. Наведемо приклади прикладних прийо­мів обчислення.

1. Прийом округлення одного або двох доданків.

49 + 26 = 98 + 27= 298+ 199 =

49 + 1=50 98 + 2 = 100 298+2 = 300

50 + 26 = 76 100 + 27=127 199 + 1=200

76–1 = 75 127–2 = 125 300 + 200 = 500

500–3 = 497

2. Прийом множення на 5.

26x5 = (26x10): 2 = 260: 2= 130

128 х 5 = (128 х 10): 2 = 1280 : 2 = 640

3. Множення на 9.

26 х 9 = (26 х 10) - 26 = 260 - 26 = 234

128 х 9 = (128 х 10) - 128 = 1280 - 128 = 1152

4. Множення на 11.

26 х 11 = (26х 10)+ 26 = 260+ 26 = 286

128 х 11 = (128 х 10) + 128 = 1280 + 128 = 1408

Ці прийоми потрібно показувати лише в тому випадку, якщо: клас оволодів основними прийомами.

Вправи в усній лічбі необхідно проводити не лише з абстракт­ ними числами, але й з іменованими, як з простими, так і з складеними. Суттєве значення при цьому має підбір прикладів:

45 грн. 25 коп. + 30 грн. 10 коп.

4м 25 см + 3 м 30 см

2 кг 200 г + 3 кг 500 г

Враховуючи те, що учні допоміжної школи швидко забувають співвідношення одиниць вимірювання, необхідно давати частіше вправи на роздроблення і перетворення, підбираючи завдання з нарос­танням ступеня складності.

Під час проведення занять з усної лічби вирішуються не лише арифметичні приклади, але й задачі. Для тренування в усному розв'я­занні арифметичних задач необхідно мати набори різноманітних наочних посібників, перш за все набори предметів для рахунку: канце­лярські приладдя, іграшки, геометричні фігури, монетні каси тощо. Усно розв'язуються в більшості випадків прості арифметичні задачі, а із складених лише ті, які можна легко конкретизувати, показати на предметах, на малюнках і кресленнях на дошці.

Ефективність оволодіння технікою усних обчислень у значній мірі залежить від дотримання системи методичних прийомів, які краще давати учням у такій послідовності.

На першому етапі учням необхідно пропонувати завдання для усної лічби з використанням конкретного матеріалу. Це може бути роздатковий матеріал, таблиці, записи на дошці тощо.

На другому етапі пропонуються завдання, розв'язання яких може супроводжуватись розгорнутим записом з обов'язковим промов­лянням записаного вголос.

На третьому етапі форма запису розв'язання приклада звужу­ється, а усний звіт про хід виконання тієї чи іншої дії дається учнями більш лаконічним.

На четвертому етапі розв'язання завдань проводиться усно, без опору на наочність і запис.