
- •2. Приведение произвольной системы сил к простейшему виду. Условия равновесия произвольной системы сил
- •3. Растяжение и сжатие стержня. Продольная сила. Условия прочности при растяжении
- •1. Матрицы и действия над ними. Определители и их свойства. Обратная матрица. Метод Крамера и Гаусса.
- •2. Модель идеального совершенного газа. Интеграл Бернулли для адиабатических течений совершенного газа. Сопло Лаваля
- •3. Плоскопараллельное движение твердого тела. Определение скоростей и ускорений точек тела
- •1. Векторные пространства. Линейная зависимость векторов. Базис. Размерность
- •3. Движение твердого тела вокруг одной неподвижной точки. Скорости и ускорения точек тела
- •1. Разностные схемы для ур-й мат физики. Явные и неявные разностные схемы, условия их устойчивости. Метод прогонки
- •2. Плоскопараллельное движение твердого тела. Определение скоростей и ускорений точек тела
- •3. Кручение стержня круглого поперечного сечения. Крутящий момент. Условия прочности и жесткости при кручении.
- •1. Линейные операторы и их матрицы. Собственные значения и собственные векторы. Нормальные формы матрицы линейного оператора
- •1. Кривые второго порядка. Их канонические уравнения
- •2. Сложное движение точки. Теоремы о сложении скоростей и ускорений
- •3. Изгиб балки. Нормальные и касательные напряжения. Условие прочности
- •Касательные напряжения в продольных сечениях балки
- •Проверка прочности и подбор сечения балки
- •1. Поверхности второго порядка. Их канонические уравнения
- •2. Уравнения Лагранжа 2-ого рода
- •3. Модель идеальной жидкости. Интегралы уравнений движения идеальной жидкости
- •2. Общие теоремы динамики точки
- •1. Элементы теории поля. Поток, дивергенция, ротор вектора. Теорема Гаусса-Остроградского. Теорема Стокса
- •2. Прямолинейные колебания материальной точки
- •2. Движение точки в поле центральных сил. Формулы Бине
- •2. Движение планет. Закон всемирного тяготения.
- •3. Энергетические методы определения перемещений. Теорема Кастилиано. Интеграл Мора. Правило Верещагина.
- •1. Формула Тейлора и ее остаточный член
- •2. Определение траектории материальной точки в ньютоновом поле тяготения. Искусственные спутники Земли
- •3. Гравитационные волны в идеальной жидкости
- •1. Ряды Фурье. Основные свойства коэффициентов Фурье. Неравенство Бесселя
- •2. Движение несвободной материальной точки. Плоский математический маятник.
- •3. Канонические уравнения метода сил при изгибе балок и рам
- •1. Теорема Вейерштрасса о равномерной сходимости функционального ряда.
- •2. Динамика относительного движения материальной точки. Относительный покой и относительное движение вблизи поверхности Земли.
- •2. Общие теоремы динамики системы
- •3. Устойчивость упругих стержней. Критическая сила
- •1. Степенные ряды и их свойства. Интервал и радиус сходимости
- •2. Динамика точки переменной массы. Уравнение Мещерского. Задача Циолковского
- •3. Слоистые течения. Течение Пуазейля, течение Куэтта, течение под действием силы тяжести
- •2. Принцип возможных перемещений
- •3. Постановка задач теории упругости в компонентах перемещений и напряжений
- •1. Достаточные условия сходимости ряда Фурье
- •2. Поверхности разрыва внутри идеальных сжимаемых сред. Адиабата Гюгонио
- •3. Плоскопараллельное движение твердого тела. Определение скоростей и ускорений точек тела
- •1. Определение интеграла Римана и достаточные условия его существования
- •2. Уравнения Лагранжа 2-ого рода
- •3. Свойство упругого равновесия изотропного тела при отсутствии массовых сил
- •2. Канонические уравнения движения системы
- •3. Основы теории пограничного слоя. Уравнения Прандтля
- •1. Элементы теории поля. Поток, дивергенция, ротор в-ра. Т-ма Гаусса-Остроградского. Т-ма Стокса
- •2. Вращение абсолютно твердого тела вокруг неподвижной оси. Давление на ось
- •3. Уравнения Ламе движения упругого тела в перемещениях
- •1. Элементы теории поля. Поток, дивергенция, ротор в-ра. Т-ма Гаусса-Остроградского. Т-ма Стокса
- •2. Движение абсолютно твердого тела, имеющего одну неподвижную точку. Кинематические уравнения Эйлера
- •3. Основы теории пограничного слоя
- •1. Группа,поле, кольцо
- •2. Динамические уравнения Эйлера
- •3. Представление решений уравнений Ламе в форме Папковича-Нейбера
- •1. Определение и примеры конформных отображений
- •2. Первые интегралы. Проблема 4-го интеграла. Элементарная теория гироскопа
- •3. Модель идеальной жидкости и газа. Интегралы уравнений движения идеальной жидкости. Сопло Лаваля
- •1. Интегральная теорема Коши
- •Доказательство
- •2. Элементарная теория гироскопов. Движение тяжелого твердого тела вокруг неподвижной точки
- •3. Кручение призматических стержней произвольного постоянного поперечного сечения
- •1. Теорема о разложении аналитической функции в ряд Тейлора
- •2. Принцип Остроградского-Гамильтона
- •3. Модель идеального совершенного газа. Интеграл Бернулли для адиабатических течений совершенного газа. Сопло Лаваля
- •1. Теорема о представимости функции рядом Лорана
- •2. Действие удара на тело, вращающееся вокруг неподвижной оси. Центр удара
- •3. Уравнения Ламе движения упругого тела в перемещениях
- •3. Кручение стержня круглого поперечного сечения. Крутящий момент. Условия прочности и жесткости при кручении.
- •1. Изолированные особые точки аналитических функций и их классификация
- •2. Общие теоремы динамики системы
- •3. Изгиб балки. Нормальные и касательные напряжения. Условие прочности
- •Касательные напряжения в продольных сечениях балки
- •Проверка прочности и подбор сечения балки
- •1. Линейное уравнение n-го порядка с постоянными коэффициентами
- •2. Динамика точки переменной массы. Уравнение Мещерского. Задачи Циолковского
- •3. Слоистые течения. Течение Пуазейля, течение Куэтта, течение под действием силы тяжести
- •1. Линейные неоднородные ду n-го порядка. Метод вариации произвольных постоянных
- •2. Теория удара системы материальных точек. Действие удара на тело, вращающееся вокруг неподвижной оси
- •3. Устойчивость упругих стержней. Критическая сила
- •2. Постановка задач теории упругости в компонентах перемещений и напряжений
- •1. Решение смешанной задачи для уравнения колебаний струны методом Фурье
- •2. Свойство упругого равновесия изотропного тела при отсутствии массовых сил
- •3. Движение несвободной материальной точки. Плоский математический маятник
- •1. Решение смешанных задач для уравнения теплопроводности методом Фурье
- •2. Динамика относительного движения материальной точки
- •3. Одномерные нестационарные течения газа и их характеристики
- •1. Классическая вероятность. Теоремы сложения и умножения. Формула полной вероятности. Биномиальное, нормальное и пуассоновское распределения
- •2. Движение твердого тела около неподвижной точки. Скорости и ускорения точек тела
- •3. Представление решений уравнений Ламе в форме Папковича-Нейбера
- •2. Движение абсолютно твердого тела, имеющего одну неподвижную точку. Кинематические уравнения Эйлера
- •3. Базовые принципы мкэ в механике деформируемого твёрдого тела
- •1. Кривизна и кручение. Формулы Френе
- •3. Основные понятия и определения мкэ. Определение и свойства матриц жёсткости, упругости, функций формы, градиентов
- •1. Классификация линейных уравнений в частных производных 2-ого порядка. Примеры уравнений основных типов
- •2. Способы генерации конечно-элементных моделей
- •3. Задача о сильном взрыве в газе
- •1. Случайные величины и их полные характеристики. Характеристическая функция случайной величины и ее свойства. Закон больших чисел
- •2. Кручение призматических стержней произвольного постоянного поперечного сечения
- •3. Приведение произвольной системы сил к простейшему виду. Условия равновесия произвольной системы сил.
- •1. Линейные однородные ду n-го порядка. Структура общего решения
- •2. Канонические уравнения движения системы
- •1. Уравнения Лапласа и Пуассона. Постановка граничных задач. Фундаментальное решение уравнения Лапласа. Функции Грина
- •2. Движение точки в поле центральных сил. Формулы Бине
- •3. Интегрирование дифференциального уравнения изогнутой оси балки
- •1. Разностные схемы для ур-й мат физики. Явные и неявные разностные схемы, условия их устойчивости. Метод прогонки
- •2. Основные этапы решения задач механики в пакетах компьютерной механики (на примере пакетов ansys и nastran)
- •3. Двумерное стационарное движение газа. Уравнение Чаплыгина
- •1. Матрицы и действия над ними. Определители и их свойства. Обратная матрица. Матричная форма записи системы линейных уравнений. Метод Крамера
- •2. Устойчивость равновесия механической системы. Теорема Дирихле
- •3. Растяжение и сжатие стержня. Продольная сила. Условия прочности при растяжении.
- •1. Разностные схемы для ур-й мат физики. Явные и неявные разностные схемы, условия их устойчивости. Метод прогонки
- •2. Принцип Остроградского-Гамильтона
- •3. Канонические уравнения метода сил при изгибе балок и рам
- •1. Численные решения систем алгебраических уравнений. Метод исключения. Метод итераций. Теорема о сходимости
- •2. Слоистые течения вязкой жидкости. Течение Пуазейля. Течение под действием силы тяжести
- •3. Движение точки в поле центральных сил. Закон всемирного тяготения
- •1. Численное решение уравнений. Метод итерации, его сходимость. Метод Ньютона, его геометричсексий смысл
- •2. Определение траектории материальной точки в ньютоновом поле тяготения. Искусственные спутники Земли
- •3. Модель вязкой жидкости. Уравнения Навье - Стокса
- •1. Численное решение оду. Метод Рунге-Кутта
- •2. Принцип возможных перемещений. Уравнение Даламбера-Лагранжа
- •3. Задача о сильном взрыве в газе
- •1. Линейное уравнение n-го порядка с постоянными коэффициентами
- •2. Общие теоремы динамики системы материальных точек
- •3. Модель идеальной жидкости. Интегралы уравнений движения идеальной жидкости
- •1. Степенные ряды и их свойства. Интервал и радиус сходимости
- •2. Динамика точки переменной массы. Уравнение Мещерского. Задача Циолковского
- •3. Трансзвуковые течения. Уравнение Эйлера–Трикоми. Особенности сверхзвукового обтекания тел
- •1. Численное решение оду. Метод Рунге- Кутта
- •2. Методы четвертого порядка точности.
- •2. Устойчивость равновесия механической системы. Теорема Дирихле
- •3. Свойство упругого равновесия изотропного тела при отсутствии массовых сил
1. Кривые второго порядка. Их канонические уравнения
Кривые
2-го порядка
определяются ур-ниями 2-й степени
относительно прямоугольной декартовой
системы координат. Общее ур-ние имеет
вид:
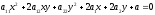 ,где
,где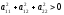
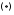
Th1:Любое
уравнение 2-го порядка вида
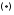 при условии
при условии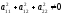 задает на пл-ти либо
эллипс,
либо гиперболу,
либо параболу,
либо пару
пересекающихся прямых,
либо пару
параллельных прямых,
либо прямую,
либо
задает на пл-ти либо
эллипс,
либо гиперболу,
либо параболу,
либо пару
пересекающихся прямых,
либо пару
параллельных прямых,
либо прямую,
либо .
.
Определение.
Если ввести новую сис-му корд-т, совершив
поворот осей на угол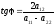 и подходящей перенос
начала коод-т, то ур-ние
и подходящей перенос
начала коод-т, то ур-ние
![]() любой невырожденной кривой 2-го порядка
м.б. приведено с следующим каноническим
видам:
любой невырожденной кривой 2-го порядка
м.б. приведено с следующим каноническим
видам:
Эллипс
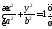 —мн-во точек на пл-ти,
для которых сумма расстояний от каждой
до фокусов равна
—мн-во точек на пл-ти,
для которых сумма расстояний от каждой
до фокусов равна .
.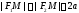
|
|
|
Гипербола
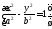 —мн-во точек на пл-ти,
для которых модуль разности расстояния
от фокусов равены
—мн-во точек на пл-ти,
для которых модуль разности расстояния
от фокусов равены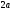 .
.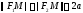
|
|
|
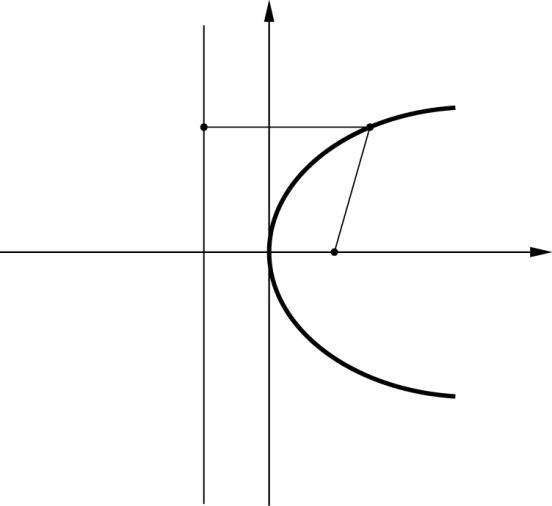
Парабола
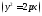 —мн-во точек на пл-ти,
каждая из которых равноудалена от фокуса
и директрисы параболы
—мн-во точек на пл-ти,
каждая из которых равноудалена от фокуса
и директрисы параболы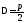 .
.
|
|
|
Уравнения
вырождающихся кривых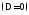 м.б. приведены к
видам:
м.б. приведены к
видам:
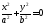 —две мнимые
пересекающиеся прямые, точка;
—две мнимые
пересекающиеся прямые, точка;
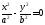 —две пересекающиеся
прямые;
—две пересекающиеся
прямые;
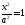 —пара параллельных
прямых;
—пара параллельных
прямых;
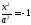 —две совпадающие
прямые;
—две совпадающие
прямые;
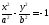 —
—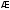 ,мнимый эллипс
,мнимый эллипс
2. Сложное движение точки. Теоремы о сложении скоростей и ускорений
Пусть имеется неподвижная
система координат (НСК) (ξ, η, ζ) и пусть
имеется ПСК и материальная точка,
движущаяся произвольным образом. Зная
движение т. М по отношению к ПСК и зная
движение ПСК относительно НСК, найти
характеристики движения материальной
т.М по отношению к НСК. 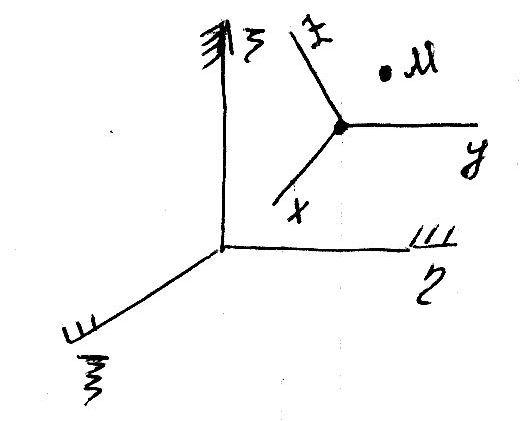
ОПР. Движение точки по отношению к подвижной системе координат называется относительным
ОПР. Движение точки по отношению к неподвижной системе координат наз абсолютным
ОПР. Движение подвижной системы координат по отношению к неподвижной наз переносным.
ОПР. Переносной скоростью и ускорениемт М наз соответственно скорость и ускорение той точки подвижной системы координат с которой в данным момент совпадает движущаяся точка.
Обозначим приращение
вектора r за время Δt: в неподвижной
системе Δr, в подвижной
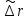
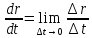 – полная,
– полная,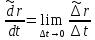 - локальная производные вектора.
- локальная производные вектора.
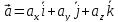 ,a,y,z
– функции времени.
,a,y,z
– функции времени.
ωxk (эти
формулы наз формулыПуансо)
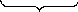

ωxj ωxi da/dt в локальной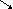
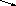
ω – угловая скорость вращения подвижн системы относительно неподвижной.
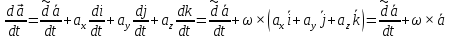 -
очевидно что фор-ла сохраняется если
подвижная система координат будет
перемещаться как свободное тело
(поступательно вместе с т 0 и вращением
вокруг нее)
-
очевидно что фор-ла сохраняется если
подвижная система координат будет
перемещаться как свободное тело
(поступательно вместе с т 0 и вращением
вокруг нее)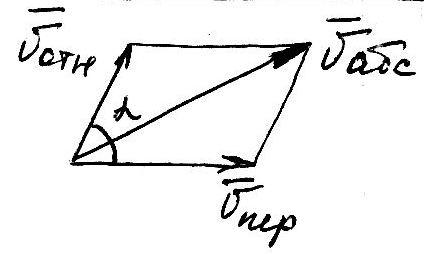
Теорема сложения скоростей.
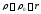 ;
;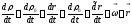
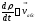 ;
;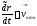 ;
;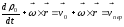 (*)
(*)
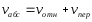
Теорема о сложении ускорений.
Продифференцируем
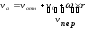
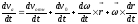
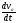 =
=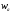 ;
;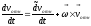 ;
;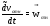 ;
;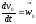 ;
;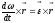 ;
;

Т.о.
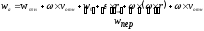 ;
;
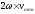 –ускорение Кориолиса(поворот)
–ускорение Кориолиса(поворот)
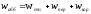
Случаи, когда
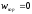 : 1.
: 1.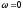 ,
т.е. ПСК не вращается;
,
т.е. ПСК не вращается;
2.
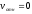 ,
т.е. точка в ПСК неподвижна;
,
т.е. точка в ПСК неподвижна;


3.
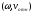 =0,
180°.
=0,
180°.
3. Изгиб балки. Нормальные и касательные напряжения. Условие прочности
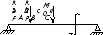 Для
проведения расчетов на прочность при
изгибе необходимо найти опасное сечение
балки, то есть сечение, гдеМпринимает
наибольшее значение. С этой целью
производится построение эпюрМиQпо длине балки. ВеличинаМв
произвольном сечении равна алгебраической
сумме моментов относительно центра
тяжести рассматриваемого сечения от
всех нагрузок, расположенных по одну
сторону от сечения. ВеличинаQравна алгебраической сумме проекций
всех сил, расположенных по одну сторону
от сечения, на направление нормали к
оси бруса в рассматриваемом сечении.Знаки:
Для
проведения расчетов на прочность при
изгибе необходимо найти опасное сечение
балки, то есть сечение, гдеМпринимает
наибольшее значение. С этой целью
производится построение эпюрМиQпо длине балки. ВеличинаМв
произвольном сечении равна алгебраической
сумме моментов относительно центра
тяжести рассматриваемого сечения от
всех нагрузок, расположенных по одну
сторону от сечения. ВеличинаQравна алгебраической сумме проекций
всех сил, расположенных по одну сторону
от сечения, на направление нормали к
оси бруса в рассматриваемом сечении.Знаки:
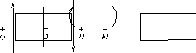 Значение
момента откладывается по нормали от
оси эпюры всегда в сторону волокон,
испытывающих при изгибе сжатие. Если
ордината оказывается сверху от оси
эпюры, изгибающему моменту приписывается
знак "+".
Значение
момента откладывается по нормали от
оси эпюры всегда в сторону волокон,
испытывающих при изгибе сжатие. Если
ордината оказывается сверху от оси
эпюры, изгибающему моменту приписывается
знак "+".
Чистый изгиб балки постоянного сечения.
Гипотеза 1. При чистом изгибе сечения балки, плоские до деформации, остаются плоскими и после деформации. Взаимное перемещение двух близко расположенных сечений сводится к повороту на некоторый угол вокруг нейтральной оси,
Гипотеза 2. Продольные слои балки при чистом изгибе не надавливают друг на друга, а испытывают лишь простое растяжение или сжатие в направлении, параллельном оси балки.
Гипотеза 3. Картина деформаций, наблюдаемая на боковой поверхности балки, не изменяется по ширине сечения. Отсюда следует постоянство нормальных напряжений по ширине сечения.
Эти гипотезы сводят реальную балку к модели, состоящей из жестких пластинок, соединенных упругими слоями, работающими на растяжение или сжатие.
Нормальные
напряжения при поперечном изгибе
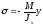 .
.
Знак
"минус" свидетельствует о том, что
положительный момент вызывает
отрицательные (сжимающие) напряжения
в верхних слоях балки, имеющих положительные
значения координаты
 .
.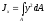 называется осевым моментом инерции
площади сечения.
называется осевым моментом инерции
площади сечения.


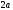 и
и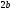 —большая и малая
оси,
—большая и малая
оси,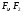 —фокусы,
—фокусы,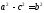 ,
,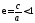 —эксцентриситет,
для окружности
—эксцентриситет,
для окружности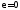 ,
,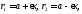 —фокальные радиусы,
—фокальные радиусы,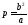 —фокальный
параметр,
—фокальный
параметр,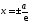 —уравнение
директрис
—уравнение
директрис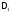 и
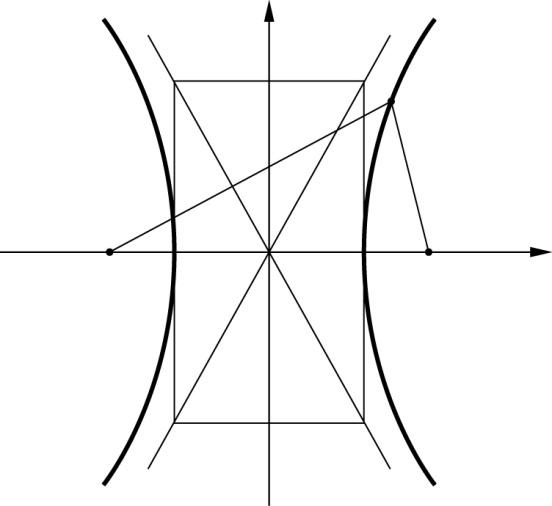
и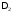 .
.
 — фокус,
— фокус, —фокусное
расстояние,
—фокусное
расстояние,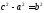 ,
,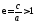 —эксцентриситет,
—эксцентриситет,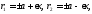 —фокальные радиусы,
—фокальные радиусы, —уравнение
директрис
—уравнение
директрис
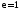 —эксцентриситет
—эксцентриситет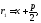 —фокальный радиус.
—фокальный радиус.