Билет 1 1. Многочлен от одной переменной. Корни многочлена. Разложение многочлена на неприводимые множители над R и С. Основная теорема алгебры

1. Кольцо многочленов от одной переменной. Корни многочлена. Разложение многочлена на неприводимые множители над R и С. Основная теорема алгебры.

Определение 2.1: Многочленом от одной переменной над кольцом K называется выражение

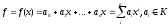где x – некоторая переменная.

Множество всех многочленов от x над кольцом K будем обозначать символом K[x]. На множестве K[x] определим операции сложения и умножения.

Теорема1. 1) Если K – кольцо, то K[x] – тоже кольцо.

2) Если K – коммутативное кольцо, то K[x] – тоже коммутативное кольцо.

3) Если K – содержит единицу, то K[x] – тоже содержит единицу.

4) Если K не имеет делителей нуля, то K[x] тоже не имеет делителей нуля.

Определение 2.2: Пусть f (x) – многочлен. Если f (c) = 0, то c называется корнем многочлена f (x).

Основная теорема алгебры: Любой многочлен с комплексными коэффициентами степени выше нулевой имеет хотя бы один комплексный корень.

След1: Всякий мног-н f(x) ∈K[x] ,deg f(x)=n>1, имеет n корней, если каждый из корней считать столько раз, какова его кратность.

След2: Число различных корней мног-на не превосходит его степени.

Теорема2: Для всякого мног-на f(x) ∈K[x] степени n больше нуля имеет место разложение на неприводимые множители вида: f(x)=a_n(x–b₁)…(x–b_s)(x²+p₁x+q₁)…(x²+p_tx+q_t), где a_n, b_k, p_j, q_j∈R; p_j² -4q_j<0 ; k=1,…,s; j=1,…,t; s≥0; t≥0; s+2t=n. Это разложение единственно с точностью до перестановки сомножителей.

Мног-н f(x) ∈K[x] степени n больше нуля со старшим коэфф., равным единице, наз. неприводимым (над полем P), если его нельзя представить в виде произведения мног-ов из P[x], степени которых меньше n. Очевидно, мног-ны над полем R вида x²+px+q, p, q∈R, p²–4q<0, а также вида x–a, a∈R, явл. неприводимыми. Над C, единственным неприводимым мног-ом явл. мног-н первой степени.

2. Приведение произвольной системы сил к простейшему виду. Условия равновесия произвольной системы сил

Статика– раздел механики, который изучает равновесие механических систем или тел под действием сил. Величина, являющаяся мерой механического взаимодействия материальных тел называетсясилой.

Основная лемма. Всякая сила, приложенная к абсолютно твёрдому телу, в данной точек А, эквивалентна той же силе, приложенной в точке В, и паре, момент которой, равен моменту силы приложенной в точке А относительно точки В.

Пусть есть произвольная система сил действующая на абсолютно твёрдое тело, расположенная как угодно в пространстве. Выберем произвольный центр О и перенесем все силы системы в этот центр. От пересечения каждой силы, мы получим силу и пару, момент которой равен моменту переносимой силы относительно выбранного центра О. Складывая все силы в центре О, получим одну результирующую силу.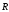

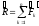(1) Складывая моменты вех пар, получим векторный момент результирующей пары :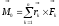(2) Величина, равная векторной сумме всехcил системы (1) называетсяглавным векторомсистемы, а величина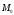, равная сумме моментов вех сил системы относительно центра О (2) называетсяглавным моментомотносительно центра О. Таким образом, любую пространственную систему сил, приведенную к центру О, заменим на приложенную в этом центре результирующей силой, равной главному вектору системыи результирующей парой, момент которой равен главному моменту системыотносительно центра приведения.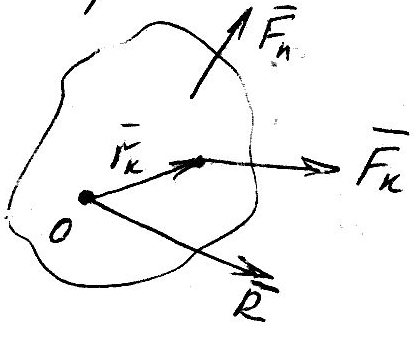

При изменении центра приведения главный вектор останется без изменений, поэтому он сам представляет собой 1-й инвариант пространственной системы сил по отношению к изменению центра приведения, т.е..

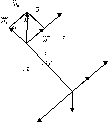
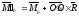=>=>=> ‑ 2-ым инвариантом системы будет скалярное произведение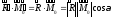, т.е проекция вектора момента на направление главного вектора постоянна и не зависит от центра приведения. Векторыиназываютсяэлементами приведениясистемы.

1) Приведем полученную систему к винту. Винт ‑ совокупность силы и пары, вектор момента которой коллинеарен силе (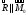), или же совокупность силы и пары сил, лежащие в ортогональных плоскостях.

Разложим исходный вектор момента на две составляющие 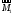и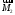. Выберем точку приведениятак, чтобы возникающий момент уравновешивал. Т.е мы можем нашу систему привести к винту, зная уравнение винтовой оси.

Т. к. , используя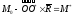, получаем.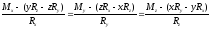

2) ,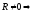в этом случае система сил приводится к одному результирующему вектору, который в таком случае называется равнодействующим. Если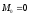, то равно действующая будет проходить через центр О.

Эти условия являются необходимыми и достаточными, чтобы система имела равнодействующую.

3) ,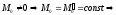главный вектор системы не зависит от выбора центра приведения. Система приводится к паре сил с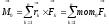, где О – произвольный центр.

4) 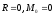‑ система сил находится в равновесии. Последние условие даёт необходимое и достаточное условие равновесия произвольной системы сил:

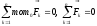(3)

Если спроектировать (3) на оси коорд-т, то для пространственной сис-мы сил получ 6 – уравнений

,,

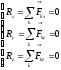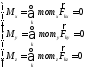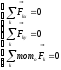
а для плоской ‑ 3 уравнения:

ТЕОРЕМА 3-х моментов. Для равновесия плоской системы сил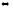сумма моментов относительно 3-х точек, не лежащих на одной прямой, равнялась 0.

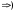Очевидно, т. к. момент относительно любой точки = 0.

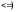
ТЕОРЕМА.Для равновесия плоской системы силсумма моментов относительно 2-х произвольных точек и сумма проекций всех сил на произвольную ось, не перпендикулярно к прямой, соединяющей эти точки = 0.

Систему сил, линии действия которых пересекаются в одной точке будем называть сходящейся.

ТЕОРЕМА. Если система сил сходящаяся, тогда пространственная система имеет 3 уравнения равновесия, а плоская – 2 уравнения.