3. Задача о сильном взрыве в газе

При взрыве газа на границе области возмущения возникает сферическая ударная волна, быстро распространяющаяся по покоящемуся газу.

Под взрывом будем понимать мгновенное выделение энергии за бесконечно малое время.

Область за ударной волной записываем в сферических координатах.

Ур неразрывности:

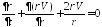
Ур движения:

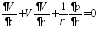
Условие адиабатичности:

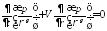
+ начальные и граничные условия.

В каждый момент времени полная энергия газа внутри сферической ударной волны складывается из энергии взрыва 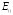и энергии газа внутриs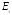

Ударная волна сильная

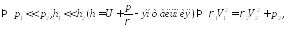
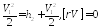
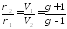Если газ совершенный, то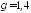

(т.к. р1 мало)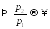

Найдем скорость распределения ударной волны:

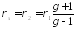Из отношений давлений ():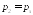

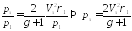
Следует отметить, что радиус возрастает прапорционально энергии и обратно прапорционально плотности. С ростом времени радиус увеличивается, а скорость ударной волны уменьшается.

Билет 48

1. Линейное уравнение n-го порядка с постоянными коэффициентами

Для линейного однородного дифференциального уравнения с постоянными коэффициентами существует простой алгоритм построения фундаментальной системы решений. Будем искать решение уравнения в виде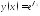. Подставляя в уравнение получим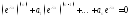Продифференцировав и сократив на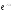получим характеристическое уравнение вида. Таким образом, задача о решении линейного однородного уравненияn -го порядка с постоянными коэффициентами сводится к решению алгебраического уравнения. Если характеристическое уравнение имеет n различных действительных корней 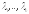, то фундаментальная система решений состоит из функций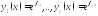 и общее решение однородного уравнения имеет вид: .

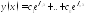Если какой-либо из действительных корней характеристического уравнения повторяется r раз (r-кратный корень), то в фундаментальной системе решений ему отвечают r функций.

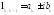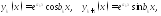_{Если характеристическое уравнение имеет} комплексные корни, то каждой паре простых (имеющих кратность 1 ) комплексных корней в фундаментальной системе решений отвечает пара функцийЕсли жекомплексная пара корней имеет кратность r, то  такой паре в фундаментальной системе решений отвечают функции

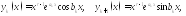
2. Общие теоремы динамики системы материальных точек

Диф. уравнения движения сис-мы:

Основная задача динамики состоит в том, что бы зная действующие силы, внешние и внутренние, определить закон движения всех точек системы.

Теорема о движении центра масс:

,=>продифференцировав дважды по t получим=>- произведение центра масс на ускорение этого центра равно сумме всех внешних сил.

Вывод: значение теоремы

она даёт обоснование динамики точки

она позволяет исключить из рассмотрения неизвестные внутренние силы

а) при отсутствии внешних сил ЦМ движется прямолинейно равномерно.

б) если внешние силы таковы что их проекция на какую-либо ось равна 0, то проекция скорости на эту ось постоянна.

Теорема об изменении количества движения сис-мы:

- главный вектор количества движения сис-мы

=>- производная по времени от количества движения сис-мы равно сумме внешних сил, действующих на сис-му. 1-ый интеграл дает при:

а) =>

б) =>

Теорема об изменении кинетического момента КМС

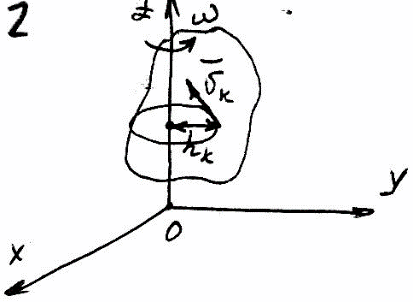
- момент инерции отн-но оси

- кинетический момент

Теорема об изменнеии кинетического момента:

Производная по времени от кинетического момента отн-но некоторого центра равна сумме моментов внешних сил отн-но того же центра.

Первые интегралы (законы сохранения):

1. - по величине и направлению

2.

Теорема об изменении кинетической энергии системы:

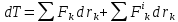(дифференциал кинетической энергии системы равняется сумме элементарных работ как внешних, так и внутренних сил, действующих на систему)