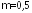- •2. Приведение произвольной системы сил к простейшему виду. Условия равновесия произвольной системы сил
- •3. Растяжение и сжатие стержня. Продольная сила. Условия прочности при растяжении
- •1. Матрицы и действия над ними. Определители и их свойства. Обратная матрица. Метод Крамера и Гаусса.
- •2. Модель идеального совершенного газа. Интеграл Бернулли для адиабатических течений совершенного газа. Сопло Лаваля
- •3. Плоскопараллельное движение твердого тела. Определение скоростей и ускорений точек тела
- •1. Векторные пространства. Линейная зависимость векторов. Базис. Размерность
- •3. Движение твердого тела вокруг одной неподвижной точки. Скорости и ускорения точек тела
- •1. Разностные схемы для ур-й мат физики. Явные и неявные разностные схемы, условия их устойчивости. Метод прогонки
- •2. Плоскопараллельное движение твердого тела. Определение скоростей и ускорений точек тела
- •3. Кручение стержня круглого поперечного сечения. Крутящий момент. Условия прочности и жесткости при кручении.
- •1. Линейные операторы и их матрицы. Собственные значения и собственные векторы. Нормальные формы матрицы линейного оператора
- •1. Кривые второго порядка. Их канонические уравнения
- •2. Сложное движение точки. Теоремы о сложении скоростей и ускорений
- •3. Изгиб балки. Нормальные и касательные напряжения. Условие прочности
- •Касательные напряжения в продольных сечениях балки
- •Проверка прочности и подбор сечения балки
- •1. Поверхности второго порядка. Их канонические уравнения
- •2. Уравнения Лагранжа 2-ого рода
- •3. Модель идеальной жидкости. Интегралы уравнений движения идеальной жидкости
- •2. Общие теоремы динамики точки
- •1. Элементы теории поля. Поток, дивергенция, ротор вектора. Теорема Гаусса-Остроградского. Теорема Стокса
- •2. Прямолинейные колебания материальной точки
- •2. Движение точки в поле центральных сил. Формулы Бине
- •2. Движение планет. Закон всемирного тяготения.
- •3. Энергетические методы определения перемещений. Теорема Кастилиано. Интеграл Мора. Правило Верещагина.
- •1. Формула Тейлора и ее остаточный член
- •2. Определение траектории материальной точки в ньютоновом поле тяготения. Искусственные спутники Земли
- •3. Гравитационные волны в идеальной жидкости
- •1. Ряды Фурье. Основные свойства коэффициентов Фурье. Неравенство Бесселя
- •2. Движение несвободной материальной точки. Плоский математический маятник.
- •3. Канонические уравнения метода сил при изгибе балок и рам
- •1. Теорема Вейерштрасса о равномерной сходимости функционального ряда.
- •2. Динамика относительного движения материальной точки. Относительный покой и относительное движение вблизи поверхности Земли.
- •2. Общие теоремы динамики системы
- •3. Устойчивость упругих стержней. Критическая сила
- •1. Степенные ряды и их свойства. Интервал и радиус сходимости
- •2. Динамика точки переменной массы. Уравнение Мещерского. Задача Циолковского
- •3. Слоистые течения. Течение Пуазейля, течение Куэтта, течение под действием силы тяжести
- •2. Принцип возможных перемещений
- •3. Постановка задач теории упругости в компонентах перемещений и напряжений
- •1. Достаточные условия сходимости ряда Фурье
- •2. Поверхности разрыва внутри идеальных сжимаемых сред. Адиабата Гюгонио
- •3. Плоскопараллельное движение твердого тела. Определение скоростей и ускорений точек тела
- •1. Определение интеграла Римана и достаточные условия его существования
- •2. Уравнения Лагранжа 2-ого рода
- •3. Свойство упругого равновесия изотропного тела при отсутствии массовых сил
- •2. Канонические уравнения движения системы
- •3. Основы теории пограничного слоя. Уравнения Прандтля
- •1. Элементы теории поля. Поток, дивергенция, ротор в-ра. Т-ма Гаусса-Остроградского. Т-ма Стокса
- •2. Вращение абсолютно твердого тела вокруг неподвижной оси. Давление на ось
- •3. Уравнения Ламе движения упругого тела в перемещениях
- •1. Элементы теории поля. Поток, дивергенция, ротор в-ра. Т-ма Гаусса-Остроградского. Т-ма Стокса
- •2. Движение абсолютно твердого тела, имеющего одну неподвижную точку. Кинематические уравнения Эйлера
- •3. Основы теории пограничного слоя
- •1. Группа,поле, кольцо
- •2. Динамические уравнения Эйлера
- •3. Представление решений уравнений Ламе в форме Папковича-Нейбера
- •1. Определение и примеры конформных отображений
- •2. Первые интегралы. Проблема 4-го интеграла. Элементарная теория гироскопа
- •3. Модель идеальной жидкости и газа. Интегралы уравнений движения идеальной жидкости. Сопло Лаваля
- •1. Интегральная теорема Коши
- •Доказательство
- •2. Элементарная теория гироскопов. Движение тяжелого твердого тела вокруг неподвижной точки
- •3. Кручение призматических стержней произвольного постоянного поперечного сечения
- •1. Теорема о разложении аналитической функции в ряд Тейлора
- •2. Принцип Остроградского-Гамильтона
- •3. Модель идеального совершенного газа. Интеграл Бернулли для адиабатических течений совершенного газа. Сопло Лаваля
- •1. Теорема о представимости функции рядом Лорана
- •2. Действие удара на тело, вращающееся вокруг неподвижной оси. Центр удара
- •3. Уравнения Ламе движения упругого тела в перемещениях
- •3. Кручение стержня круглого поперечного сечения. Крутящий момент. Условия прочности и жесткости при кручении.
- •1. Изолированные особые точки аналитических функций и их классификация
- •2. Общие теоремы динамики системы
- •3. Изгиб балки. Нормальные и касательные напряжения. Условие прочности
- •Касательные напряжения в продольных сечениях балки
- •Проверка прочности и подбор сечения балки
- •1. Линейное уравнение n-го порядка с постоянными коэффициентами
- •2. Динамика точки переменной массы. Уравнение Мещерского. Задачи Циолковского
- •3. Слоистые течения. Течение Пуазейля, течение Куэтта, течение под действием силы тяжести
- •1. Линейные неоднородные ду n-го порядка. Метод вариации произвольных постоянных
- •2. Теория удара системы материальных точек. Действие удара на тело, вращающееся вокруг неподвижной оси
- •3. Устойчивость упругих стержней. Критическая сила
- •2. Постановка задач теории упругости в компонентах перемещений и напряжений
- •1. Решение смешанной задачи для уравнения колебаний струны методом Фурье
- •2. Свойство упругого равновесия изотропного тела при отсутствии массовых сил
- •3. Движение несвободной материальной точки. Плоский математический маятник
- •1. Решение смешанных задач для уравнения теплопроводности методом Фурье
- •2. Динамика относительного движения материальной точки
- •3. Одномерные нестационарные течения газа и их характеристики
- •1. Классическая вероятность. Теоремы сложения и умножения. Формула полной вероятности. Биномиальное, нормальное и пуассоновское распределения
- •2. Движение твердого тела около неподвижной точки. Скорости и ускорения точек тела
- •3. Представление решений уравнений Ламе в форме Папковича-Нейбера
- •2. Движение абсолютно твердого тела, имеющего одну неподвижную точку. Кинематические уравнения Эйлера
- •3. Базовые принципы мкэ в механике деформируемого твёрдого тела
- •1. Кривизна и кручение. Формулы Френе
- •3. Основные понятия и определения мкэ. Определение и свойства матриц жёсткости, упругости, функций формы, градиентов
- •1. Классификация линейных уравнений в частных производных 2-ого порядка. Примеры уравнений основных типов
- •2. Способы генерации конечно-элементных моделей
- •3. Задача о сильном взрыве в газе
- •1. Случайные величины и их полные характеристики. Характеристическая функция случайной величины и ее свойства. Закон больших чисел
- •2. Кручение призматических стержней произвольного постоянного поперечного сечения
- •3. Приведение произвольной системы сил к простейшему виду. Условия равновесия произвольной системы сил.
- •1. Линейные однородные ду n-го порядка. Структура общего решения
- •2. Канонические уравнения движения системы
- •1. Уравнения Лапласа и Пуассона. Постановка граничных задач. Фундаментальное решение уравнения Лапласа. Функции Грина
- •2. Движение точки в поле центральных сил. Формулы Бине
- •3. Интегрирование дифференциального уравнения изогнутой оси балки
- •1. Разностные схемы для ур-й мат физики. Явные и неявные разностные схемы, условия их устойчивости. Метод прогонки
- •2. Основные этапы решения задач механики в пакетах компьютерной механики (на примере пакетов ansys и nastran)
- •3. Двумерное стационарное движение газа. Уравнение Чаплыгина
- •1. Матрицы и действия над ними. Определители и их свойства. Обратная матрица. Матричная форма записи системы линейных уравнений. Метод Крамера
- •2. Устойчивость равновесия механической системы. Теорема Дирихле
- •3. Растяжение и сжатие стержня. Продольная сила. Условия прочности при растяжении.
- •1. Разностные схемы для ур-й мат физики. Явные и неявные разностные схемы, условия их устойчивости. Метод прогонки
- •2. Принцип Остроградского-Гамильтона
- •3. Канонические уравнения метода сил при изгибе балок и рам
- •1. Численные решения систем алгебраических уравнений. Метод исключения. Метод итераций. Теорема о сходимости
- •2. Слоистые течения вязкой жидкости. Течение Пуазейля. Течение под действием силы тяжести
- •3. Движение точки в поле центральных сил. Закон всемирного тяготения
- •1. Численное решение уравнений. Метод итерации, его сходимость. Метод Ньютона, его геометричсексий смысл
- •2. Определение траектории материальной точки в ньютоновом поле тяготения. Искусственные спутники Земли
- •3. Модель вязкой жидкости. Уравнения Навье - Стокса
- •1. Численное решение оду. Метод Рунге-Кутта
- •2. Принцип возможных перемещений. Уравнение Даламбера-Лагранжа
- •3. Задача о сильном взрыве в газе
- •1. Линейное уравнение n-го порядка с постоянными коэффициентами
- •2. Общие теоремы динамики системы материальных точек
- •3. Модель идеальной жидкости. Интегралы уравнений движения идеальной жидкости
- •1. Степенные ряды и их свойства. Интервал и радиус сходимости
- •2. Динамика точки переменной массы. Уравнение Мещерского. Задача Циолковского
- •3. Трансзвуковые течения. Уравнение Эйлера–Трикоми. Особенности сверхзвукового обтекания тел
- •1. Численное решение оду. Метод Рунге- Кутта
- •2. Методы четвертого порядка точности.
- •2. Устойчивость равновесия механической системы. Теорема Дирихле
- •3. Свойство упругого равновесия изотропного тела при отсутствии массовых сил
3. Слоистые течения. Течение Пуазейля, течение Куэтта, течение под действием силы тяжести
Класс точных решений урвынений Новье-Стокса давольно узок.
1.Течение
Куэтта- течение между параллельными
стенками,одна из которых движется с
постоянной скоростью
![]()
Массовые
силы отсутствуют,движение жидкости
между стенками называют движением
верхней границы.
![]()
![]()
![]()
![]() ;
;![]() ;
;![]() ;
=>
;
=>
![]()
![]() =>
=>![]() =>
=>![]() ;
;
![]() -
начальные
условия
-
начальные
условия
![]()
Стационарное
решение:
![]() ;
;![]() из 1го условия
из 1го условия
![]()
![]() -
линейный профиль;
-
линейный профиль;
![]() -
значение Ньютона
-
значение Ньютона
Расход
жидкости через поперечное сечение
![]() :
:
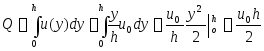
Средняя скорость-расход жидкости на площадь попер. Сечения
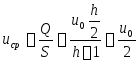
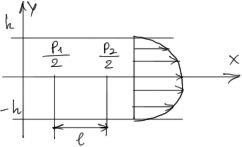
2. Течение между двумя параллельными стенками под действиемперепада давления- течение Пуазейля.
![]() ;
;
![]()
Решение
ищем в виде:
![]()
![]()
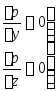 -
уравнение неразрывности тождественно
выполняется =>
-
уравнение неразрывности тождественно
выполняется =>
![]()
При
![]() при
при![]() -
условие прилипания.
-
условие прилипания.
![]() -
стационарная задача
-
стационарная задача ![]() делим на
делим на![]() :
:
![]()
![]()
![]() ;
;
![]()
![]()
![]() =>
=>
![]() h
всегда>y Максимальная
скорость при y=0
h
всегда>y Максимальная
скорость при y=0
3. Течение вязкой жидкости под действием силы тяжести.
Линии тока параллельны OX:
![]()

![]() (
(![]() ;
;![]() )
)
![]()
Граничные условия:
![]()
![]() -
свободная поверхность ;
-
свободная поверхность ;
![]() -
уравнение неразрывности;
-
уравнение неразрывности;![]() (нормальные
напряжения) касательные=0 т.к.
(нормальные
напряжения) касательные=0 т.к.![]() - отсутствуют касательные напряжения
- отсутствуют касательные напряжения
![]()
![]()
Будем
считать, что движение формируется лишь
под действием силы тяжести:
![]()
а
![]() -стационарная задача
-стационарная задача
![]()
![]()
![]() при y=h
при y=h
![]() при
при
![]()
![]() ;
;![]() при
при![]()
Билет 31
1. Линейные неоднородные ду n-го порядка. Метод вариации произвольных постоянных
Линейное
неоднородное ДУ n-го
порядка имеет вид

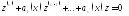 соотв
ЛОДУ. С помощью Линейного диф-го
оператора можно переписать в виде
соотв
ЛОДУ. С помощью Линейного диф-го
оператора можно переписать в виде

Теорема
Если
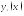 частное решение (1), а
частное решение (1), а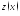 -
любое решение 2, то
-
любое решение 2, то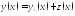 решение (1).
решение (1).
Теорема об общем решении ЛОДУ.
Если
 ФСР то любое решение допускает
представление
ФСР то любое решение допускает
представление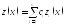
Теорема
об общем решении ЛНДУ. Если
 ФСР ЛОДУ, а
ФСР ЛОДУ, а![]() частное решение (1), то
частное решение (1), то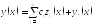 .
.
Теорема Лагранжа (метод вариации произвольной постоянной)
Если
для ЛОДУ (2) известна ФСР
![]() то при любом неоднородном члене
то при любом неоднородном члене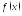 решение уравнения (1) выразиться при
помощи квадратур над изв функциями
решение уравнения (1) выразиться при
помощи квадратур над изв функциями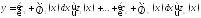 =
=
2. Теория удара системы материальных точек. Действие удара на тело, вращающееся вокруг неподвижной оси
Пусть твердое тело
может вращаться вокруг неподвижной
оси, которую примем за ось z
прямоугольной системы координат Oxyz,
связанной с телом. Если на это тело
подействовал ударный импульс активных
сил, то он вызовет ударные импульсы
реакций, проходящих через эту ось. Т.к.
этот случай движения можно рассматривать
как движение твердого тела, имеющего
две неподвижные точки
A
и B,
то ударные импульсы реакции оси можно
свести к двум импульсам
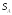 и
и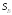 ,
приложенных в соответствующих точках.
Теоремы об изменении количества движения
и кинетического момента дадут уравнения:
,
приложенных в соответствующих точках.
Теоремы об изменении количества движения
и кинетического момента дадут уравнения:
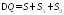
 т.к
т.к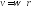 ,
то
,
то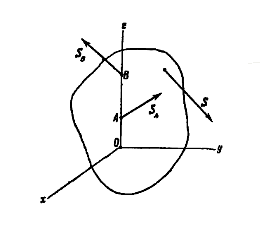

Здесь М – масса тела,
а
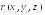 -
радиус-вектор центра масс С.
-
радиус-вектор центра масс С.
![]()
![]()
![]()
![]()

Определим условия при которых ударный импульс не действует на ось вращения, т.е. когда:
![]()
![]()
![]()
При таком выборе сис-мы
координат:
![]()
![]()
![]()
![]()
Итак, для того чтобы ударный импульс не передавался на ось необходимо вып. след. условий:
1) Ось вращения должна быть главной осью инерции для одной из своих точек О.
2) Ударный импульс лежит в плоскости перпендикулярной к оси вращения и прох. через точку О.
3) Ударный импульс перпендикулярен плоскости прох. через центр масс и ось вращения.
4) Точка пересечения ударного импульса с этой плоскостью должна находиться с той же стороны от оси вращения, что и центр масс и отстоять на расстоянии η
3. Устойчивость упругих стержней. Критическая сила
Устойчивость первого рода нарушение устойчивости равновесия деформируемых тел, происходящее вследствие отклонений от формы равновесия, которые не могут быть вызваны действующей нагрузкой.
Устойчивость второго рода нарушение устойчивости, происходящее вследствие того, что сопротивление деформированию с возрастанием нагрузки уменьшается или остается постоянным ввиду возникновения пластических деформаций.
Наиболее общий случай потери устойчивости первого рода для сжатых стержней любого профиля изгибная форма устойчивости.
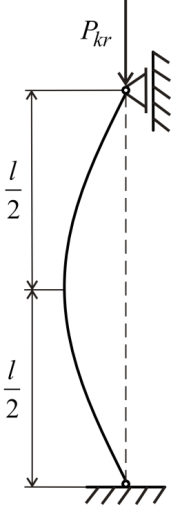
Рассмотрим
прямолинейный стержень с шарнирно-закрепленными
концами, показанный на рисунке 1, сжатый
силой
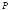 .
.
Рисунок
1
Стержень с шарнирно-закрепленными
концами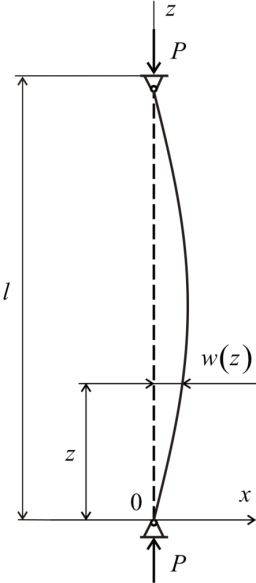
Отклонение от
прямолинейно формы равновесия состоит
в искривлении оси стержня. В этом случае
для любого сечения имеем 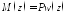 . (1)
. (1)
На основании
дифференциальной зависимости между
прогибом и изгибающим моментом (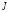
момент инерции сечения относительно
нейтральной оси)
момент инерции сечения относительно
нейтральной оси)
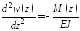 ,
или с учетом формулы (1)
,
или с учетом формулы (1)
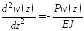 .
.
Обозначим
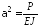 .
Тогда
.
Тогда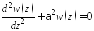 .
.
Отсюда
 .
.
Из граничных условий
имеем 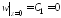 ,
,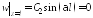 .
.
Таким образом
 .
(2) Выражение (2) описывает критическое
состояние и позволяет найти критическую
силу
.
(2) Выражение (2) описывает критическое
состояние и позволяет найти критическую
силу
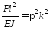 ,
,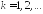
Практический интерес
представляет наименьшая критическая
сила ( ):
): .
(3)
.
(3)
Формула (3) впервые
получена Л. Эйлером, поэтому критическая
сила
 называется также эйлеровой критической
силой.
называется также эйлеровой критической
силой.
Критическую силу в
случае любого закрепления концов стержня
можно определить по формуле (3), если в
ней длину стержня заменить длиной
полуволны синусоиды, по которой изгибается
стержень при данном закреплении.
Обозначим длину полуволны
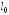 .
Тогда
.
Тогда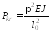 . В
рассмотренных нами случаях имеем:
. В
рассмотренных нами случаях имеем:
а) при шарнирном
закреплении концов, показанном на
рисунке
 ,
,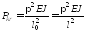 (количество длин полуволн показано на
рисунке 2, а);
(количество длин полуволн показано на
рисунке 2, а);
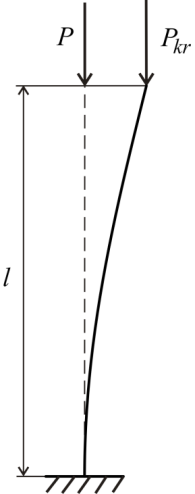
б) при заделке одного
конца стержня
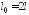 ,
, (количество длин полуволн показано на
рисунке 2, б);
(количество длин полуволн показано на
рисунке 2, б);
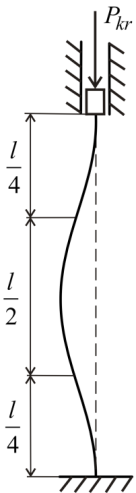
в) при шарнирном
закреплении одного конца стержня и
защемлении другого конца
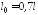 ,
, (количество длин полуволн показано на
рисунке 2, в);
(количество длин полуволн показано на
рисунке 2, в);
г) при заделке двух
концов стержня
 ,
,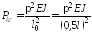 (количество длин полуволн показано на
рисунке 2, г);
(количество длин полуволн показано на
рисунке 2, г);
|
а
|
б
|
в
|
г
|
|
|
|
|
|
|
Рисунок 2 Количество длин полуволн для стержней с различными закреплениями концов | |||
Т.о, формула Эйлера
(3) для определения критической силы
принимает вид:  ,
(4)
,
(4)
где

коэффициент приведения длины.
коэффициент приведения длины.
Для шарнирно
закрепленного стержня
 ,
для стержня с заделанными концами
,
для стержня с заделанными концами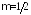 ;
для стержня с одним заделанным и другим
свободным концом
;
для стержня с одним заделанным и другим
свободным концом ;
для стержня с одним заделанным и другим
шарнирно закрепленным концом
;
для стержня с одним заделанным и другим
шарнирно закрепленным концом .
.
Отметим, что по
формуле (4) критическую силу следует
вычислять по значению главного
центрального момента инерции
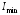 (за исключением случаев, когда закрепления
концов стержня в различных плоскостях
различны).
(за исключением случаев, когда закрепления
концов стержня в различных плоскостях
различны).
Билет 32 1. Решение задачи Коши для уравнения колебаний струны методом характеристик
Рассм.
однор. волновое ур-е:
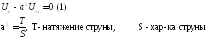
Струна
– натянутая нить, не сопротивляющ.
Изгибу НУ:
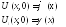 (2)
(2)
Ур-е характеристик
для (1):
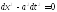
Это
ур-е раскладывается на 2:
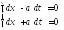
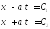
Введем
новые переменные:
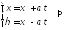 ур. колеб. струны в кан. виде:
ур. колеб. струны в кан. виде:
Общий
интеграл (3) имеет вид:

Переходим к старым переменным, получим:
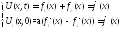
Интегрируя
2-е равенство получим:
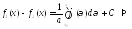 получим:
получим:
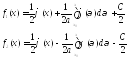

С
физической т. зрения общ реш
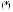 з. Коши для беск. струны предст. собой
суперпозицию 2-х волн:
з. Коши для беск. струны предст. собой
суперпозицию 2-х волн:
 Решение
Решение
![]() м.
представить в виде суммы:
м.
представить в виде суммы:
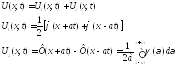
Если
нач. скор
 равна 0, то отклон.
равна 0, то отклон.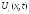 есть сумма левой и правой бегущих волн,
причем нач. форма обеих волн опред.
ф-цией 0.5
есть сумма левой и правой бегущих волн,
причем нач. форма обеих волн опред.
ф-цией 0.5 = половине нач. отклонения.
= половине нач. отклонения.
Если
![]() =0,
то
=0,
то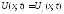 представляет возмущ. струны, создаваемое
ноч. скоростью.
представляет возмущ. струны, создаваемое
ноч. скоростью.