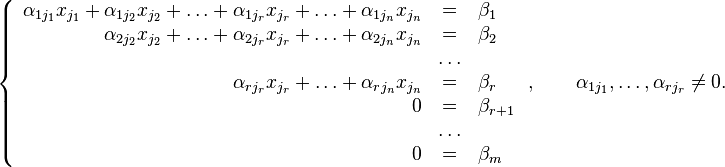- •2. Приведение произвольной системы сил к простейшему виду. Условия равновесия произвольной системы сил
- •3. Растяжение и сжатие стержня. Продольная сила. Условия прочности при растяжении
- •1. Матрицы и действия над ними. Определители и их свойства. Обратная матрица. Метод Крамера и Гаусса.
- •2. Модель идеального совершенного газа. Интеграл Бернулли для адиабатических течений совершенного газа. Сопло Лаваля
- •3. Плоскопараллельное движение твердого тела. Определение скоростей и ускорений точек тела
- •1. Векторные пространства. Линейная зависимость векторов. Базис. Размерность
- •3. Движение твердого тела вокруг одной неподвижной точки. Скорости и ускорения точек тела
- •1. Разностные схемы для ур-й мат физики. Явные и неявные разностные схемы, условия их устойчивости. Метод прогонки
- •2. Плоскопараллельное движение твердого тела. Определение скоростей и ускорений точек тела
- •3. Кручение стержня круглого поперечного сечения. Крутящий момент. Условия прочности и жесткости при кручении.
- •1. Линейные операторы и их матрицы. Собственные значения и собственные векторы. Нормальные формы матрицы линейного оператора
- •1. Кривые второго порядка. Их канонические уравнения
- •2. Сложное движение точки. Теоремы о сложении скоростей и ускорений
- •3. Изгиб балки. Нормальные и касательные напряжения. Условие прочности
- •Касательные напряжения в продольных сечениях балки
- •Проверка прочности и подбор сечения балки
- •1. Поверхности второго порядка. Их канонические уравнения
- •2. Уравнения Лагранжа 2-ого рода
- •3. Модель идеальной жидкости. Интегралы уравнений движения идеальной жидкости
- •2. Общие теоремы динамики точки
- •1. Элементы теории поля. Поток, дивергенция, ротор вектора. Теорема Гаусса-Остроградского. Теорема Стокса
- •2. Прямолинейные колебания материальной точки
- •2. Движение точки в поле центральных сил. Формулы Бине
- •2. Движение планет. Закон всемирного тяготения.
- •3. Энергетические методы определения перемещений. Теорема Кастилиано. Интеграл Мора. Правило Верещагина.
- •1. Формула Тейлора и ее остаточный член
- •2. Определение траектории материальной точки в ньютоновом поле тяготения. Искусственные спутники Земли
- •3. Гравитационные волны в идеальной жидкости
- •1. Ряды Фурье. Основные свойства коэффициентов Фурье. Неравенство Бесселя
- •2. Движение несвободной материальной точки. Плоский математический маятник.
- •3. Канонические уравнения метода сил при изгибе балок и рам
- •1. Теорема Вейерштрасса о равномерной сходимости функционального ряда.
- •2. Динамика относительного движения материальной точки. Относительный покой и относительное движение вблизи поверхности Земли.
- •2. Общие теоремы динамики системы
- •3. Устойчивость упругих стержней. Критическая сила
- •1. Степенные ряды и их свойства. Интервал и радиус сходимости
- •2. Динамика точки переменной массы. Уравнение Мещерского. Задача Циолковского
- •3. Слоистые течения. Течение Пуазейля, течение Куэтта, течение под действием силы тяжести
- •2. Принцип возможных перемещений
- •3. Постановка задач теории упругости в компонентах перемещений и напряжений
- •1. Достаточные условия сходимости ряда Фурье
- •2. Поверхности разрыва внутри идеальных сжимаемых сред. Адиабата Гюгонио
- •3. Плоскопараллельное движение твердого тела. Определение скоростей и ускорений точек тела
- •1. Определение интеграла Римана и достаточные условия его существования
- •2. Уравнения Лагранжа 2-ого рода
- •3. Свойство упругого равновесия изотропного тела при отсутствии массовых сил
- •2. Канонические уравнения движения системы
- •3. Основы теории пограничного слоя. Уравнения Прандтля
- •1. Элементы теории поля. Поток, дивергенция, ротор в-ра. Т-ма Гаусса-Остроградского. Т-ма Стокса
- •2. Вращение абсолютно твердого тела вокруг неподвижной оси. Давление на ось
- •3. Уравнения Ламе движения упругого тела в перемещениях
- •1. Элементы теории поля. Поток, дивергенция, ротор в-ра. Т-ма Гаусса-Остроградского. Т-ма Стокса
- •2. Движение абсолютно твердого тела, имеющего одну неподвижную точку. Кинематические уравнения Эйлера
- •3. Основы теории пограничного слоя
- •1. Группа,поле, кольцо
- •2. Динамические уравнения Эйлера
- •3. Представление решений уравнений Ламе в форме Папковича-Нейбера
- •1. Определение и примеры конформных отображений
- •2. Первые интегралы. Проблема 4-го интеграла. Элементарная теория гироскопа
- •3. Модель идеальной жидкости и газа. Интегралы уравнений движения идеальной жидкости. Сопло Лаваля
- •1. Интегральная теорема Коши
- •Доказательство
- •2. Элементарная теория гироскопов. Движение тяжелого твердого тела вокруг неподвижной точки
- •3. Кручение призматических стержней произвольного постоянного поперечного сечения
- •1. Теорема о разложении аналитической функции в ряд Тейлора
- •2. Принцип Остроградского-Гамильтона
- •3. Модель идеального совершенного газа. Интеграл Бернулли для адиабатических течений совершенного газа. Сопло Лаваля
- •1. Теорема о представимости функции рядом Лорана
- •2. Действие удара на тело, вращающееся вокруг неподвижной оси. Центр удара
- •3. Уравнения Ламе движения упругого тела в перемещениях
- •3. Кручение стержня круглого поперечного сечения. Крутящий момент. Условия прочности и жесткости при кручении.
- •1. Изолированные особые точки аналитических функций и их классификация
- •2. Общие теоремы динамики системы
- •3. Изгиб балки. Нормальные и касательные напряжения. Условие прочности
- •Касательные напряжения в продольных сечениях балки
- •Проверка прочности и подбор сечения балки
- •1. Линейное уравнение n-го порядка с постоянными коэффициентами
- •2. Динамика точки переменной массы. Уравнение Мещерского. Задачи Циолковского
- •3. Слоистые течения. Течение Пуазейля, течение Куэтта, течение под действием силы тяжести
- •1. Линейные неоднородные ду n-го порядка. Метод вариации произвольных постоянных
- •2. Теория удара системы материальных точек. Действие удара на тело, вращающееся вокруг неподвижной оси
- •3. Устойчивость упругих стержней. Критическая сила
- •2. Постановка задач теории упругости в компонентах перемещений и напряжений
- •1. Решение смешанной задачи для уравнения колебаний струны методом Фурье
- •2. Свойство упругого равновесия изотропного тела при отсутствии массовых сил
- •3. Движение несвободной материальной точки. Плоский математический маятник
- •1. Решение смешанных задач для уравнения теплопроводности методом Фурье
- •2. Динамика относительного движения материальной точки
- •3. Одномерные нестационарные течения газа и их характеристики
- •1. Классическая вероятность. Теоремы сложения и умножения. Формула полной вероятности. Биномиальное, нормальное и пуассоновское распределения
- •2. Движение твердого тела около неподвижной точки. Скорости и ускорения точек тела
- •3. Представление решений уравнений Ламе в форме Папковича-Нейбера
- •2. Движение абсолютно твердого тела, имеющего одну неподвижную точку. Кинематические уравнения Эйлера
- •3. Базовые принципы мкэ в механике деформируемого твёрдого тела
- •1. Кривизна и кручение. Формулы Френе
- •3. Основные понятия и определения мкэ. Определение и свойства матриц жёсткости, упругости, функций формы, градиентов
- •1. Классификация линейных уравнений в частных производных 2-ого порядка. Примеры уравнений основных типов
- •2. Способы генерации конечно-элементных моделей
- •3. Задача о сильном взрыве в газе
- •1. Случайные величины и их полные характеристики. Характеристическая функция случайной величины и ее свойства. Закон больших чисел
- •2. Кручение призматических стержней произвольного постоянного поперечного сечения
- •3. Приведение произвольной системы сил к простейшему виду. Условия равновесия произвольной системы сил.
- •1. Линейные однородные ду n-го порядка. Структура общего решения
- •2. Канонические уравнения движения системы
- •1. Уравнения Лапласа и Пуассона. Постановка граничных задач. Фундаментальное решение уравнения Лапласа. Функции Грина
- •2. Движение точки в поле центральных сил. Формулы Бине
- •3. Интегрирование дифференциального уравнения изогнутой оси балки
- •1. Разностные схемы для ур-й мат физики. Явные и неявные разностные схемы, условия их устойчивости. Метод прогонки
- •2. Основные этапы решения задач механики в пакетах компьютерной механики (на примере пакетов ansys и nastran)
- •3. Двумерное стационарное движение газа. Уравнение Чаплыгина
- •1. Матрицы и действия над ними. Определители и их свойства. Обратная матрица. Матричная форма записи системы линейных уравнений. Метод Крамера
- •2. Устойчивость равновесия механической системы. Теорема Дирихле
- •3. Растяжение и сжатие стержня. Продольная сила. Условия прочности при растяжении.
- •1. Разностные схемы для ур-й мат физики. Явные и неявные разностные схемы, условия их устойчивости. Метод прогонки
- •2. Принцип Остроградского-Гамильтона
- •3. Канонические уравнения метода сил при изгибе балок и рам
- •1. Численные решения систем алгебраических уравнений. Метод исключения. Метод итераций. Теорема о сходимости
- •2. Слоистые течения вязкой жидкости. Течение Пуазейля. Течение под действием силы тяжести
- •3. Движение точки в поле центральных сил. Закон всемирного тяготения
- •1. Численное решение уравнений. Метод итерации, его сходимость. Метод Ньютона, его геометричсексий смысл
- •2. Определение траектории материальной точки в ньютоновом поле тяготения. Искусственные спутники Земли
- •3. Модель вязкой жидкости. Уравнения Навье - Стокса
- •1. Численное решение оду. Метод Рунге-Кутта
- •2. Принцип возможных перемещений. Уравнение Даламбера-Лагранжа
- •3. Задача о сильном взрыве в газе
- •1. Линейное уравнение n-го порядка с постоянными коэффициентами
- •2. Общие теоремы динамики системы материальных точек
- •3. Модель идеальной жидкости. Интегралы уравнений движения идеальной жидкости
- •1. Степенные ряды и их свойства. Интервал и радиус сходимости
- •2. Динамика точки переменной массы. Уравнение Мещерского. Задача Циолковского
- •3. Трансзвуковые течения. Уравнение Эйлера–Трикоми. Особенности сверхзвукового обтекания тел
- •1. Численное решение оду. Метод Рунге- Кутта
- •2. Методы четвертого порядка точности.
- •2. Устойчивость равновесия механической системы. Теорема Дирихле
- •3. Свойство упругого равновесия изотропного тела при отсутствии массовых сил
3. Растяжение и сжатие стержня. Продольная сила. Условия прочности при растяжении
Внутренние
усилия и характер деформаций при
растяжении и сжатии абсолютно аналогичны
и равноценны, а отличаются только
направлением. Условимся считать
положительными усилия и деформации
растяжения, а при сжатии эти же величины
будем считать отрицательными ( -
нормальная составляющая,
-
нормальная составляющая, - касательные составляющие полного
напряженияp,
где p=FA
(A-
площадь
наклонного сечения (напр, рис. в),
A=A0/cosα)
).
- касательные составляющие полного
напряженияp,
где p=FA
(A-
площадь
наклонного сечения (напр, рис. в),
A=A0/cosα)
).
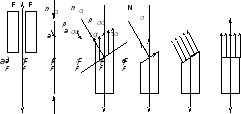
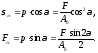
Связь между σα,
τα
и наибольшим нормальным напряжением
(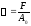 )
)
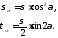
Эта
зависимость носит также название закона
парности касательных напряжений.

Для
расчета на прочность наибольший интерес
представляют площадки, перпендикулярные
оси, в которых действуют наибольшие
нормальные напряжения σ.
Равнодействующая N
этих напряжений называется продольной
силой. Для
определения нормальных напряжений
необходимо строить эпюру продольных
сил.Вектор положительной продольной
силы направлен вдоль внешней нормали
к площадке, т.е. «от площадки». Он вызывает
растяжение стержня. Вектор отрицательной
продольной силы N
направлен «к площадке».Прочность детали
при простом растяжении (сжатии) можно
оценить, сравнивая действующие в ней
максимальные напряжения с предельными
напряжениями, определяемыми для данного
материала экспериментальным путем.
Предельными напряжениями считаются
такие, при которых хрупкий материал
разрушается
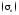 ,
а пластичный материал получает недопустимо
большие пластические деформации - течет
,
а пластичный материал получает недопустимо
большие пластические деформации - течет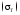 .
.
Формула проверки прочности: σ = P/F ≤ [σ]. Формула проверки грузоподъёмности: P ≤ [σ] F.
Формула определения необходимых размеров по условию прочности: F ≥ Р/[σ].
EF – жесткость, E - модуль Юнга. Проверка стрежня на жёсткость: ε = N/EF ≤ [ε].
Закон Гука для стержня: ΔL = PL/EF
Билет 2
1. Матрицы и действия над ними. Определители и их свойства. Обратная матрица. Метод Крамера и Гаусса.
Действия
над матрицами:
сложение (вычитание), умножение матрицы
на число, произведение двух матриц
(число столбцов первой из которых равно
числу строк второй, ассоциативно,
дистрибутивно, но не коммутативно (если
выполняется коммутативность, то матрицы
перестановочные)) (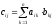 ).
).
Опр
1.1: Матрица
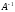 называетсяобратной
по отношению к квадратной матрице
называетсяобратной
по отношению к квадратной матрице
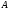 ,
если
,
если
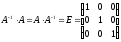 .Обратная
матрица существует только для квадратной
матрицы, определитель которой не равен
нулю.
.Обратная
матрица существует только для квадратной
матрицы, определитель которой не равен
нулю.
Опр1.2: Определитель - это многочлен, комбинирующий элементы квадратной матрицы таким образом, что его значение сохраняется при транспонировании и линейных комбинациях строк или столбцов. Т.е., определитель характеризует содержание матрицы. В частности, если в матрице есть линейно-зависимые строки или столбцы определитель равен нулю. Определитель играет ключевую роль в решении в общем виде систем линейных уравнений, на его основе вводятся базовые понятия.
Свойства определителя:
1. Если переставить две строки (или два столбца) определителя, то определитель изменит знак.
2. Если соответствующие элементы двух столбцов (или двух строк) определителя равны или пропорциональны, то определитель равен нулю.
3. Значение определителя не изменится, если поменять местами строки и столбцы, сохранив их порядок.
4. Если все элементы какой-либо строки (или столбца) имеют общий множитель, то его можно вынести за знак определителя.
5. Значение определителя не изменится, если к элементам одной строки (или столбца) прибавить соответствующие элементы другой строки (или столбца), умноженные на одно и то же число.
Метод Крамера: Рассмотрим
систему уравнений 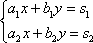
На
первом шаге вычислим определитель 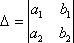 ,
его
называют главным
определителем системы.
,
его
называют главным
определителем системы.
Если ![]() ,
то
система имеет бесконечно много решений
или несовместна (не имеет решений). В
этом случае правило Крамера не поможет,
нужно использовать метод
Гаусса.
,
то
система имеет бесконечно много решений
или несовместна (не имеет решений). В
этом случае правило Крамера не поможет,
нужно использовать метод
Гаусса.
Если ![]() ,
то
система имеет единственное решение, и
для нахождения корней мы должны вычислить
еще два определителя:
,
то
система имеет единственное решение, и
для нахождения корней мы должны вычислить
еще два определителя:
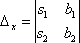 и
и 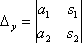
На
практике вышеуказанные определители
также могут обозначаться латинской
буквой ![]() .
.
Корни
уравнения находим по формулам:
![]() ,
, ![]()
Метод Гаусса: Сущность этого метода состоит в том, что посредством последовательных исключений неизвестных данная система превращается в ступенчатую (в частности, треугольную) систему, равносильную данной. При практическом решении задачи, расширенная матрица системы с помощью элементарных преобразований над ее строками приводится к ступенчатому виду. Далее последовательно находятся все неизвестные, начиная снизу вверх.