2.ВИЗНАЧЕНИЙ ІНТЕГРАЛ

2.1.ПОНЯТТЯ ВИЗНАЧЕНОГО ІНТЕГРАЛА, ЙОГО ГЕОМЕТРИЧНИЙ ЗМІСТ

Нехай функція y = f(x) неперервна на відрізку[a, b]. Розіб’ємо довільно цей відрізок на n частин точками a = x0 < x1 < x2 < … < xn = b. Візьмемо на кожному з відрізків довільну точку xiÎ[xi – 1, xi] (i = 1, 2, …, n), обчислимо значення функціїf(xi) і помножимо його на величину

Dxi = xi - xi – 1 (рис. 2.1).

Інтегральною сумою для функції y = f(x) на відрізку [a, b] називається сума

i =1

Границя інтегральної суми, знайдена при n ® ¥ за умови, що довжина найбільшого частинного відрізка прямує до нуля, називається визначеним інтегралом Рімана (Г. Ріман - німецький математик ХІХ ст.) від функції y = f(x) на відрізку [a, b] і позначається так:

Числа a і b називаються нижньою і верхньою межами інтегрування.

Рис. 2.1

ДВНЗ “Українська академія банківської справи НБУ”

26

Теорема Коші (достатня умова інтегрованості функції).

Якщо функція f(x) неперервна на відрізку [a, b], то вона інтегрована на цьому відрізку, тобто границя інтегральної суми існує, не залежить від способу розбиття відрізка [a, b] на частинні відрізки Dxi і вибору на них точок xi

Геометричний зміст визначеного інтеграла. Визначений інтег-

рал від невід’ємної функціїчисельно дорівнюєплощі криволінійної трапеції (фігури, обмеженої графіком функції y = f(x), віссю Ox і двома прямими x = a, x = b). Визначений інтеграл від довільної функції дорівнює алгебраїчній сумі площ, що лежать вище і нижче осіOx. Площі, що лежать вище осіOx, ввійдуть у цю суму зі знаком “+”, а площі, що лежать нижче осі Ox, - зі знаком “-”.

Економічний зміст визначеного інтеграла. Якщо f(t) - про-

T

дуктивність праці у момент часуt, то ò f (t)dt - обсяг виробленої за

0

проміжок часу [0, T] продукції.

2.2.ВЛАСТИВОСТІ ВИЗНАЧЕНОГО ІНТЕГРАЛА

1.Сталий множник А можна виносити за знак інтеграла

5. Якщо функція f(x) інтегрована на кожному з відрізків [a, c], [c, b], то

Переходячи до границі при max Dxi ® 0, одержимо співвідношення (2.7).

ДВНЗ “Українська академія банківської справи НБУ”

27

Якщо a < b < c, то на підставі властивостей 5 і 3 одержимо

Þ ò f (x)dx =ò f (x)dx -ò f (x)dx = ò f (x)dx +ò f (x)dx.

a a b a c

Геометрична ілюстрація властивості. Якщо f(x) ³ 0 на відріз-

ку [a, b] і a < c < b, то площа S криволінійної трапеції на відрізку[a, b] дорівнює сумі площ S1 + S2 трапецій на відрізках [a, c] і [c, b] (рис. 2.2). £

y

y = f (x)

Рис. 2.2

6. Якщо на відрізку [a, b], де a < b, виконується нерівність j(x) £ f(x), то

тому що f(xi) ³ j(xi) і Dxi ³ 0.

З останньої нерівності випливає формула (2.8). £

y

y = f (x)

y =j (x)

Рис. 2.3

ДВНЗ “Українська академія банківської справи НБУ”

28

Геометрична ілюстрація властивості. Якщо 0 £ j(x) £ f(x), то площа криволінійної трапеції, обмеженої верхньою кривоюf(x), не менше площі, обмеженої нижньою кривою j(x) (рис. 2.3).

7.Якщо m і M - найменше й найбільше значення функції f(x) на відрізку

[a, b] і a < b, то

Геометрична ілюстрація властивості. Площа S криволінійної трапеції, обмеженої кривою f(x), не менше площі S1 прямокутника висотою m і не більше площі S2 прямокутника висотою M (рис. 2.4).

Наслідок. Нехай функція f(x) неперервна на відрізку [- a, a]. Тоді

8. Теорема про середнє значення визначеного інтеграла.

Якщо функція f(x) неперервна на відрізку [a, b] і a < b, то існує хоча б одна точка с Î [a, b] така, що

ДВНЗ “Українська академія банківської справи НБУ”

29

w Якщо m і M - найменше і найбільше значення функціїf(x) на відрізку [a, b] і a < b, то з властивості 7 випливає, що

Оскільки f(x) неперервна на відрізку [a, b], то вона приймає всі значення між m і M. Отже, при деякому значенні c Î [a, b] буде

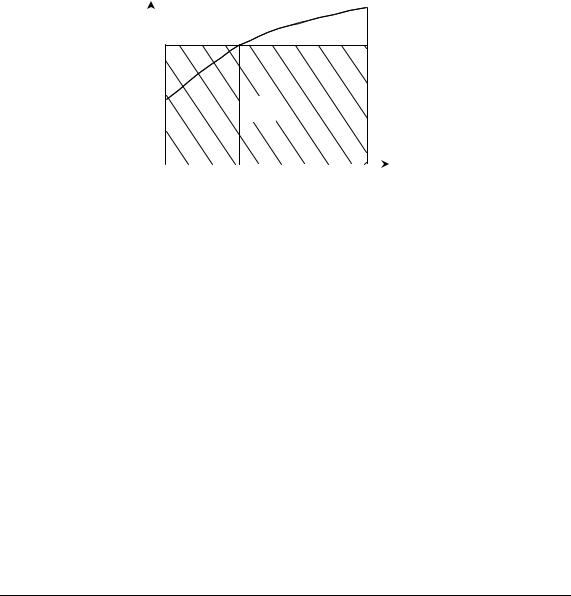
Геометрична ілюстрація властивості. Якщо f(x) ³ 0 на відрізку

[a, b], то знайдеться така точкас Î [a, b], що площа, обмежена кривою f(x), дорівнюватиме площі прямокутника з висотою f(с) (рис. 2.5).

Рис. 2.5

Середнім значенням функції f(x) на відрізку [a, b] називається число:

9.Значення визначеного інтеграла не залежить відпозначення змінної інтегрування:

2.3. ДИФЕРЕНЦІЮВАННЯ ВИЗНАЧЕНОГО ІНТЕГРАЛА ЗІ ЗМІННОЮ ВЕРХНЬОЮ МЕЖЕЮ

Розглянемо інтеграл від функціїf(x) на відрізку [a, x], де a – фіксоване число, а x - змінне. Такий інтеграл буде функцією верхньої межі

ДВНЗ “Українська академія банківської справи НБУ”

30

Теорема. Якщо f(x) - неперервна функція, а Ф(x) визначається за формулою (2.13), то Ф¢(x) = f(x), тобто похідна визначеного інтеграла зі змінною верхньою межею дорівнює значенню підінтегральної функції у точці диференціювання

Рис. 2.6

w Надамо аргументу x приросту Dx, тоді функція Ф(x) одержить приріст (рис. 2.6)

(до останнього інтеграла застосували теорему про середнє значення визначеного інтеграла).

Обчислимо границю

Теорема існування невизначеного інтеграла. Для будь-якої неперервної на відрізку [a, b] функції f(x) існує первісна й невизначений інтеграл

x

w Якщо f(x) неперервна на відрізку [a, b] і Ф (x) = ò f (t)dt, то

a

Ф¢(x) = f(x), тобто Ф(x) є первісною для f(x) на [a, b]. Але тоді існує невизначений інтеграл

a

Формула (2.15) зв’язує невизначений інтеграл із визначеним інтегралом із змінною верхньою межею.

ДВНЗ “Українська академія банківської справи НБУ”

31