4.2.3. Ознака Д’Аламбера

w а) припустимо, що l < 1. Оберемо число q так, що l < q < 1. Тоді можна знайти такий номерN, що для усіх n >N виконується нерів-

ність < q Þ un < qun – 1. Застосовуючи цю нерівність для n = N + 1, n = N + 2, ... одержуємо:

uN +1 < quN , uN +2 < quN +1 < q2uN , ...,uN + k < q k uN ,... .

¥¥

менником, меншим за одиницю), тому за теоремою 2 пункту 4.2.2 збіга-

¥ ¥

ється і ряд åu N +k , і, як наслідок, збігається і ряд åun (за теоремою 1

n ® ¥

хідна умова збіжності). £

ДВНЗ “Українська академія банківської справи НБУ”

116

Зауваження. При l = 1 ознака Д’Аламбера не дає відповіді на запитання про збіжність ряду(ряд у цьому випадку може бути як розбіжним, так і збіжним).

Приклад 4.8. За ознакою Д’Аламбера дослідимо збіжністьря

Отже, ряд збігається (враховуємо, що (п + 1)! = п!(п + 1)). <

4.2.4. Радикальна ознака Коші

¥

Теорема 5. Якщо для ряду åun , ип ≥ 0 існує границя

n = 1

lim n un = l,

n®¥

¥

то при l < 1 ряд åun збігається, а при l > 1 розбігається

n =1

w а) припустимо, що l < 1. Оберемо число q таке, що l < q < 1. Тоді можна знайти такий номерN, що для всіх n > N виконується не-

¥

рівність nun < q Þ un < qn. Оскільки ряд åqn збігається, то за пер-

n = 0

¥

шою ознакою порівняння збігається і рядåuN + k , тоді за теоремою 1

k =1

¥

пункту 4.1.2 збігається ряд åun ;

n=1

б) припустимо тепер, що l > 1, тоді для усіх п, більших деякого N, n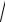un > 1, тобто ип > 1. Отже, не виконується необхідна умова збіж-

¥

ності, і ряд åun розбігається. £

n = 1

Зауваження 1. Також, як в ознаці Д’Аламбера, при l = 1 радикальна ознака Коші не дає відповіді на запитання про збіжність ряду.

Зауваження 2. Якщо для одного й того ж ряду існують границі за ознаками Д’Аламбера та Коші, то вони дорівнюють одна одній.

ДВНЗ “Українська академія банківської справи НБУ”

117