B

p = f (j)

східчастого сектора. Оскільки ця сума є інтегральною сумою для функції r2(j)/2 на відрізку [a, b], то її границя при max Dji ® 0 є визначеним інтегралом

Зауваження. Для замкнутої кривої, що охоплює полюс, полярний кут j змінюється від 0 до 2p.

Приклад 2.5. Обчислити площу, обмежену лінією r = 3 + cosj, 0 £ j £ 2p.

► З урахуванням симетрії фігури одержимо за формулою (2.26):

2.7.2. Обчислення довжини дуги кривої

Обчислення довжини дуги кривої у декартових координатах

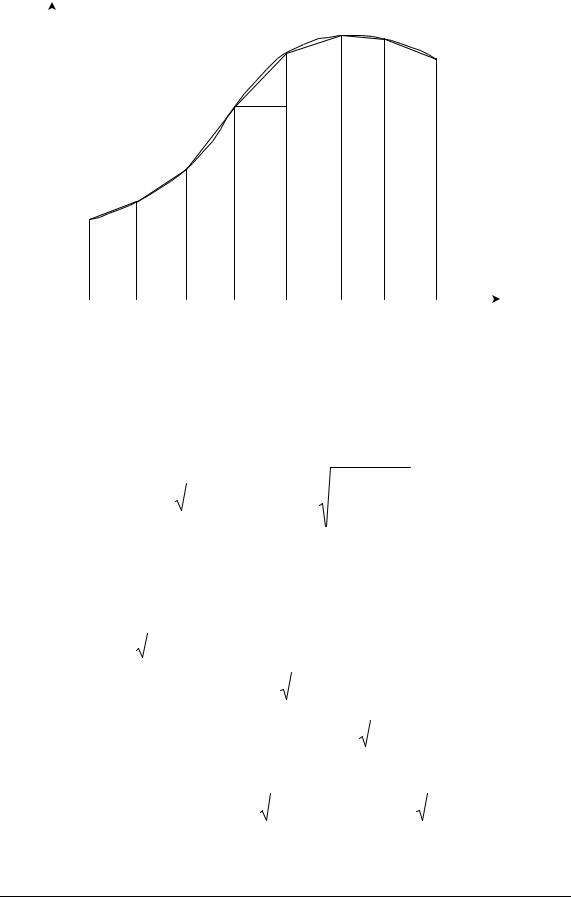
Нехай на відрізку [a, b] плоска крива задана рівнянням y = f(x), де f(x) - неперервна разом із похідною функція. Тоді довжина дуги АВ (рис. 2.13) обчислюється за формулою

a

ДВНЗ “Українська академія банківської справи НБУ”

37

Рис. 2.13

w Для доведення формули(2.27) розіб’ємо дугу АВ на n частин точками A0 = A, A1,…, An = B і проведемо хордиA0A1, A1A2, …, An–1An довжини яких позначимо Dl1, Dl2, …, Dln. Довжину i-ї хорди подамо у вигляді

ДВНЗ “Українська академія банківської справи НБУ”

38

Приклад 2.7. Обчислити довжину дуги кривої y = x2 - 1 ln x при

4 2

1£ x £ e.

►Довжину дуги кривої обчислюємо за формулою (2.27):

Обчислення довжини дуги кривої, заданої параметричними рівняннями

Довжина дуги плоскої кривої, яка задана параметричними рівняннями

де x(t) і y(t) - неперервні на [a, b] функції, що мають неперервні похідні, обчислюється за формулою

a

w Дійсно, рівняння (2.28) визначають деяку функцію y = f(x), що

має неперервну похідну dy = y¢(t) . Введемо у формулі(2.27) заміну dx x¢(t)

змінної

a

ДВНЗ “Українська академія банківської справи НБУ”

39

Зауваження. Довжина дуги просторової лінії, заданої параметричними рівняннями x = x(t), y = y(t), z = z(t) (a £ t £ b), де x(t), y(t), z(t) - неперервно диференційовані на [a, b] функції, обчислюється за формулою

a

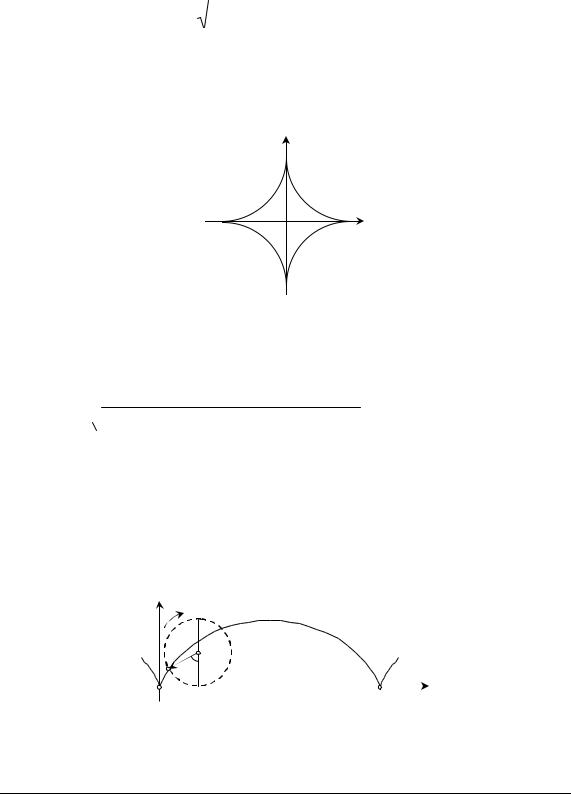
Приклад 2.8. Обчислити довжину дуги астроїди (рис. 2.14) x =a=cos3 t, y asin3 t (0 £t £2р).

y a

-a

Рис. 2.14. Астроїда

► Крива симетрична відносно осей координат, тому обчислимо за формулою (2.29) довжину 1/4 частини астроїди, розташованої у першій чверті, і результат помножимо на 4:

р/ 2 р/ 2

l = 4 ò(-3a cos2 t sin t)2 + (3a sin 2 t cos t)2 dt = 12a òsin t cos tdt =

Приклад 2.9. Обчислити довжину однієї арки циклоїди x = a(t -sint), y = a(1 - cos t), 0 £ t £ 2 р (рис. 2.15).

a

t a

Рис. 2.15. Циклоїда

ДВНЗ “Українська академія банківської справи НБУ”

40