Приклад 2.29. Знайти обсяг продукції V, виробленої за проміжок часу

► Якщо f(t) - продуктивність праці у момент часуt, то обсяг виробленої за проміжок часу [t1, t2] продукції обчислюється за формулою:

2.10. ПОДВІЙНІ ІНТЕГРАЛИ

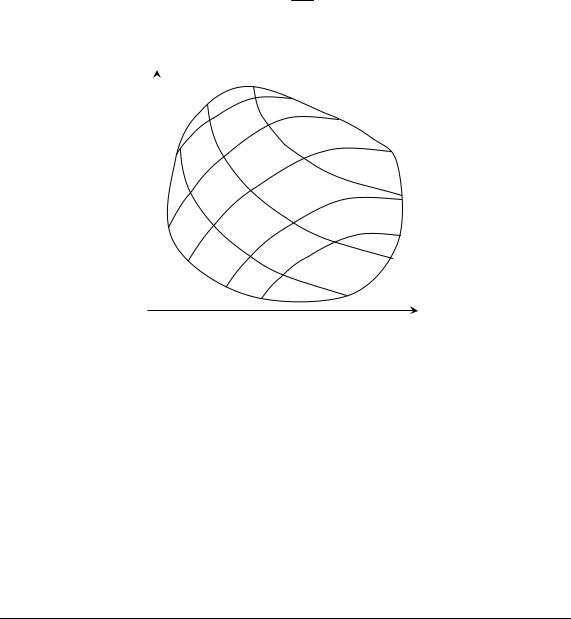
Нехай у замкненій обмеженій областіD площини xОy задана неперервна функція z = f(x, y). Розіб’ємо область D на n областей Di

довільної форми із площами Si (i =1, n ) (рис. 2.24). Діаметром di області Di називається довжина найбільшої з хорд, що з’єднує точки її межі.

y

D

Di

Pi

Рис. 2.24

У кожній з областей Di (усередині чи на її межі) візьмемо довільну точку Pi(xi, yi) і складемо суму

яка називається інтегральною сумою Рімана для функції f (x, y) в області D.

Якщо існує границя послідовності інтегральних сум(2.47) при n ® ∞ іmax di ® 0, яка не залежить від способу розбиття областіD

ДВНЗ “Українська академія банківської справи НБУ”

54

на елементарні підобласті й вибору точокPi, то вона називається по-

двійним інтегралом і позначається так:

Область D називається областю інтегрування, x, y – змінними інтегрування, f(x, y) – підінтегральною функцією, f(x, y)ds – підінтегральним виразом.

Теорема (перша достатня ознакаіснування подвійного інтеграла). Якщо f(x, y) – неперервна в замкненій обмеженій області D із кусково-гладкою межею, то подвійний інтеграл (2.48) існує

Геометричний зміст подвійного інтеграла

Інтегральна сума (2.47) при f (x, y) ³ 0 являє собою суму об’ємів

циліндрів з основами Si й висотами f(Pi). Тому при f(x, y) ³ 0 подвійний інтеграл (2.48) чисельно дорівнює об’єму тіла, обмеженого поверхнею z = f (x, y), площиною z = 0 і циліндричною поверхнею, твірна якої паралельна осі Оz, а напрямною є межа L області D (рис. 2.25).

z

z = f (z, y)

z = f (P)

y

D

x

Рис. 2.25

Якщо f(x, y) змінює знак в області D, то подвійний інтеграл (2.48) дорівнює алгебраїчній сумі об’ємів, що лежать вище й нижче площини z = 0.

ДВНЗ “Українська академія банківської справи НБУ”

55

Зауваження. Якщо в (2.48) покласти f(P) = 1, то одержимо вираз площі плоскої області D через подвійний інтеграл:

Властивості подвійного інтеграла

1. Сталий множник А можна виносити за знак подвійного інтеграла:

2.Якщо f1(x, y) і f2(x, y) інтегровані в області D, то в цій області інтегровані й функції f1(x, y) ± f2(x, y), при цьому

3.Якщо область D розбита на дві області D1 і D2 без спільних внутрішніх точок й функція f(x, y) неперервна в області D, то

w Інтегральну суму по області D можна подати у вигляді:

å f (Pi )DSi = å f (Pi )DSi + å f (Pi )DSi ,

6.Якщо інтегрована в областіD функція f(x, y) задовольняє нерівності: m ≤ f(x, y) ≤ M, то

ДВНЗ “Українська академія банківської справи НБУ”

56

7. Теорема про середнє значення подвійного інтеграла.

Подвійний інтеграл від неперервної функціїf(x, y) по області D дорівнює добутку площі S області D на значення функції f у деякій точці P Î D:

8.Якщо функція f(x, y) інтегрована в області D, то в цій області інтегрована і функція |f(x, y)|, й виконується нерівність:

w Інтегральна сума по області D задовольняє нерівності:

å f (Pi )DSi £ å| f (Pi ) | DSi ,

звідки за допомогою граничного переходу при max DSi ® 0 отримаємо нерівність (2.57). £

9.Подвійний інтеграл по областіD не залежить від позначення змінних інтегрування:

Обчислення подвійного інтеграла

Область D називається правильною (опуклою) у напрямку осі Oy (Ox),

якщо будь-яка пряма, що паралельна осі Oy (Ox), перетинає границю області не більш ніж у двох точках. Область, правильна й у напрямку осі Оx і в напрямку Оy, називається правильною (опуклою) областю.

На рис. 2.26 зображена область D, правильна в напрямку осіОy, але неправильна в напрямку осіОх, а на рис. 2.27 - область D правильна в напрямку осі Оx, але неправильна в напрямку осі Оy.

ДВНЗ “Українська академія банківської справи НБУ”

57

Правильна в напрямку осі Oy область D визначається системою нерівностей: a £ x £ b, j1 (x) £ y £ j2 (x), а правильна в напрямку осі

Ox - системою нерівностей: c £ y £ d , y1 ( y) £ x £y 2 ( y).

Зведемо обчислення подвійного інтеграла до обчислення двох простих інтегралів. Розглянемо спочатку правильну область D, у якій задана неперервна функція z = f(x, y). Припустимо, що f(x, y) ³ 0 і скористаємося геометричним змістом подвійного інтеграла. Розсічемо тіло площиною x = const, паралельною площині yОz, і позначимо площу перетину S(x). Тоді об’єм тіла можна обчислити за формулою:

a

Знайдемо площу перетину S(x). Оскільки x = const, то можна вважати z функцією тільки від y, тоді

Другий і третій інтеграли у правій частині називаються двократними (повторними) інтегралами.

Порядок обчислення подвійного інтеграла. Обчислення повто-

рного інтеграла починається з обчислення внутрішнього інтеграла.

ДВНЗ “Українська академія банківської справи НБУ”

58

Якщо перше інтегрування проводиться по зміннійy, то x вважається сталою, а межі y1 і y2 є функціями від x і навпаки.

Нехай область D правильна у напрямку осі Оy (рис. 2.26).

1.Знайти рівняння y1 = φ1(x) нижньої частини межі (нижня межа інтегрування внутрішнього інтеграла) і рівняння y2 = φ2(x) верхньої частини межі (верхня межа внутрішнього інтеграла).

2.Знайти крайні ліву (a) й праву (b) точки проекції на вісь Ох області D – нижню й верхню межі зовнішнього інтеграла і записати повторний інтеграл:

3.Обчислити внутрішній інтеграл поy, вважаючи x = const, потім замість y підставити верхню межу і відняти значення первісної, якій замість y підставлена нижня межа. У результаті утвориться функція, що залежить тільки відx, яку слід проінтегрувати поx від a до b.

Приклад 2.30. Обчислити òò(x2 + y)dxdy, де областьD обмежена

D

лініями: y = 2x - 8, y = 4x – x2.

► Координати точок перетину параболи y = 4x – x2 і прямої y = 2x - 8 знайдені у прикладі 2.3, а область D зображена на рис. 2.11. Зведемо подвійний інтеграл до повторного. Область D є правильною, однак внутрішній інтеграл зручно обчислювати по змінній y.

ДВНЗ “Українська академія банківської справи НБУ”

59