37. Назначение хвостового оперения. Балансировочная зависимость. Общий подход к выбору оперения в начальном приближении.

В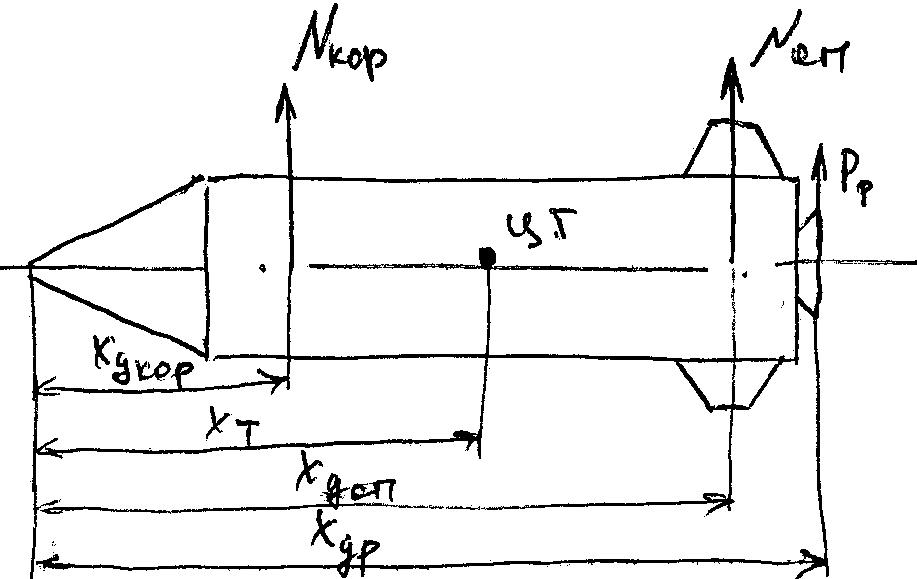ыбор оперения ЛА

Рассмотрим балансировочную зависимость для ЛА.

Рассмотрим моменты действующие на ЛА в состоянии балансировки. Под состоянием балансировки понимается ЛА, на который действует нулевой момент(а нашем случае момент тангажа).

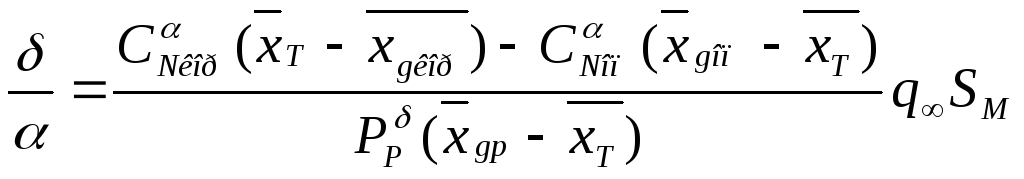
-если для -большой, значит при малых α ЛА тяжело управляется на траектории и требует значительные запасы энергии для решения вопросов управл. ЛА на траектории;

-при малых отношениях ЛА становится очень чувствительным к управлению, а значит и к воздействию возмущающих моментов, при этом возникают трудности по реализации малых углов атаки. С другой стороны СУ постоянно вынуждена компенсировать действие моментов. При этом ЛА совершает большие колебания относительно заданного углового положения в пространстве, что ухудшает его летные характеристики, приводит к большим нормальным перегрузкам действующим на ЛА, и также увеличивает затраты на управление.

Н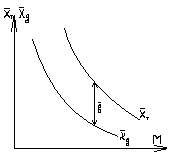еобходимо найти компромисс между устойчивостью и управляемостью. В абсолютном смысле задача выбора оперения может быть решена, как оптимизационная задача при рассмотрении всей траектории движения.L=max,ΔV_ПОТЕРЬ=min. Чтобы определить необходимо задавать шесть связей на основании которых могут быть определены параметры оперения. Часть параметров оперения задают по рекомендациям. Площадь консоли вычисляется исходя из заданной степени статической устойчивости. Сужение крыла выбирают исходя из. Заданную степень статической устойчивости -.,. Если>0, то реализуются некоторые статические неустойчивости. Если<0, то некоторые статические устойчивости.

В силу того, что в процессе полета меняется положение центра давления величина получается переменной на траектории, в силу этого выбирают для нескольких характерных точек на траектории. Такими точками могут быть: 1.начало полета(); 2.; 3.. наиболее критическая точка определяет выбор оперения.

Процесс выбора оперения включает в себя этапы: 1.выбрать ; 2.опеределение; 3.выбрать; 4.

39.ОПИШИТЕ С ПРИВЕДЕНИЕМ ОБОСНОВАНИЙ, КАКИЕ ПРЕДПОЛОЖЕНИЯ МОГУТ БЫТЬ СФОРМУЛИРОВАНЫ ОБ УСТРОЙСТВЕ И СВОЙСТВАХ НЕИЗВЕСТНОГО ОБЪЕТКА ПРИ НАЛИЧИИ ЛИШЬ ЕГО МАТЕМАТИЧЕСКОГО ОПИСАНИЯ В ВИДЕ ЛИНЕЙНОГО ОБЫКНОВЕННОГО ДИФФЕРЕНЦИАЛЬНОГО УРАВНЕНИЯ ВЫСОКГО(ВЫШЕ ВТОРОГО) ПОРЯДКА

Линейное обыкновенное ДУ высокого порядка можно представить в виде

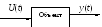(1)

Этому урав-ию соответствует функциональная схема:

U(t) – внешнее воздействие (входной сигнал)

y(t) – выходной сигнал (вых. переменная, определяющая поведение объекта в окр. среде)

1. Если в ДУ (1) коэфф-ты (a_i,i= 0,1,…,nиb) постоянны во времени, то объект явл-сястационарным, т.е. его конструктивные параметры и хар-ки, по которым вычисляются конкретные значения коэфф-в ур-я (1), во времени не изменяются.

2. Т.к. ДУ (1) получается свёрткой системы из ДУ, описывающая динамику внутренних процессов различной физической природы в объекте, которые взаимодействшуют между собой как показано на схеме

то значит, что объект явл-ся системой, т.е. состоит из внутренних взаимодействующих функциональных элементов.

Примечание: В ТАУ ДУ (1), описывающее изменение вых. сигналаy(t)в зависимости от изменения вход. сигналаU(t), принято называть динамическим звеномn-го порядка. Приn2 ДУ называют типовыми (элементарными) динамическими звеньями. Т.е. можно сказать, что объект представляет собой систему из взаимодействующих динамических звеньев, в т.ч. типовых.

Иллюстрирующий пример:Угловое дв-ие ЛА по тангажу. Функциональная схема:

И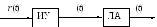У – исполнительное устройство (рулевой привод с органом управления полётом);

r(t) – командный (задающий) сигнал от сист. упр-я полётом; (t) – угол поворота органа упр-я; (t) – угол тангажа .

Линеаризованные уравнения в отклонениях от номинальных значений (p=d/dt):

для ЛА:; для ИУ:.

После свёрки получается:

или с абстрактными обозначениями коэфф-в:

или обозначениями ;:

По ДУ (1) можно исследовать динамические и статические свойства объекта.

3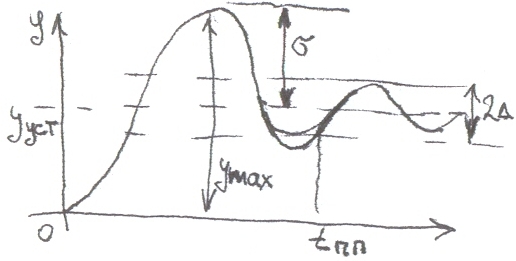. О динамических свойствах судят по переходной хар-ке, т.е. по изменению вых. сигналаy(t) при подаче на вход типового вход. Сигнала в виде ступенькиU(t) =1(t), где=const,.

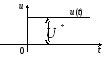
- перерегулирование;- время переходного процесса.

График изменения y(t) при заданном входеU(t) можно найти (построить): численным интегрированием ДУ (1); аналитическим решением ДУ (1).

Решение ур-я (1) ввиду его линейности имеет вид: , где- общее решение однородного ДУ, полученого из (1) приU(t)0. Функцияописывает собственное (или свободное) движение объекта из отклоненного состояния.

- частное решение ДУ (1), неоднородного, т.е. при конкретном виде функцииU(t)0. Функцияописывает установившиеся вынужденное движ-ие под воздействиемU(t).

Функция определяется выражением:(2), где_i,i= 1,2,…,n -корни характеристического ур-я(3);_i,i= 1,2,…,n – произвольные константы, определяемые по заданным ненулевым значениям начальных условий.

Выражение (2) для изменяет вид в зависимости от типа корней_i, которые могут быть действительными (вещественными) или попарно комплектно-сопряженными.

Например: Пустьn=3 и характ-ое ур-еимеет корни;;. Тогда выражение (2) принимает вид(4). Если в (4)<0 и<0, т.е. все корни располагаются справа от мнимой оси на комплексной плоскости корней хар-го ур-я (3), то все все слагаемые в (2), а значит иприбудут стремится к нулю . Т.е. система из отклоненного состояния будут возвращаться в первоначальное состояние, т.е. онаустойчива.

В рассмотренном примере (n=3) корни могут располагаться как показано на рисунках:

- степень устойчивости.

- колебательностью.

Чем больше , т.е. чем дальше корни от мнимой оси, тем быстрее завершается переходный процесс (уменьшается). Чем больше, тем сильнее колебания в переходном процессе (возрастает перерегулирование).

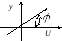4. Статические свойства опред-ся статической харак-ой (- это график зависимости установившихся значенийот величины постоян. значений). Ур-е статической харак-и получается из ДУ, если в ур-ии (1) все производные приравнять к нулю. Ур-е (1) тогда принимает вид алгебраического ур-яи график ст-ой хар-и:

41.ОПИШИТЕ С ПРИВЕДЕНИЕМ ОБОСНОВАНИЯ СПОСОБЫ И ПОСЛЕДОВАТЕЛЬНОСТЬ ПРОВЕДЕНИЯ ИССЛЕДОВАНИЙ ПРИ ТЕОРЕТИЧЕСКОМ ОПРЕДЕЛЕНИИ СТАТИЧЕСКИХ И ДИНАМИЧЕСКИХ СВОЙСТВ ЛИНЕЙНОЙ СТАЦИОНАРНОЙ СИСТЕМЫ С СОСРЕДОТОЧЕННЫМИ ПАРАМЕТРАМИ ПО ЕЕ МАТЕМАТИЧЕСКОЙ МОДЕЛИ.

1. Исследование свойств линейной стационарной САУ по корням характеристического уравнения.

Линейное Д.У. высокого порядка можно представить в виде:

(1)

Решение уравнения 1 в виду его линейности имеет вид: y(t)= y_с(t)+ y_в(t), где y_с(t) – общее решение однородного ДУ полученного из (1) при =0 функцияy_с(t) описывает собственное(свободное) движение объекта; y_в(t) – частное решение ДУ(1) неоднородного т. е. при конкретном виде функции . Функцияy_в(t) описывает установившееся вынужденное движение под воздействием .

Функция y_с(t) определяется выражением: , г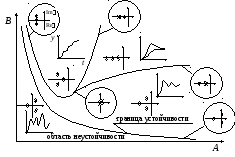де λ корни характеристического уравнения:

Корни характеристического уравнения (они же полюса ПФ Ф(s)) будут определять вид переходной характеристики замкнутой САУ. Для системы 3-го порядка (n = 3) это наглядно иллюстрирует диаграмма И.В.Вышнеградского, выполненная им в 1876 г. (см. рисунок). Эта диаграмма получается из анализа уравнения

, (2)

полученного из (2) при n = 3 введением новой переменной . При этом, коэффициенты в (2), называемые параметрами Вышнеградского, определяются формулами

,.

Диаграмма показывает, как зависит вид переходного процесса (переходной характеристики) от расположения корней характеристического уравнения (т.е. полюсов ПФ) на комплексной плоскости. Аналогичные диаграммы могут быть построены и для систем более высокого порядка.

В теории САУ наибольшее распространение получили следующие корневые оценки качества:

- степень устойчивости ; - колебательность  .

Эти оценки имеют смысл только для устойчивых систем. Поэтому представляя все корни характеристического уравнения в общем виде ,

полагая для вещественных корней _i = 0, определение для рассматриваемых корневых оценок формулируется следующим образом ,.

Н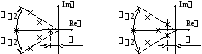агляднее это иллюстрируется графически на комплексной плоскости корней. Например, дляn = 5 показано на рисунке.

Исследование свойств линейной стационарной САУ по ПФ (по коэффициентам ПФ).

Определение корней степенных алгебраических уравнений высокого порядка является трудноразрешимой задачей без использования вычислительной техники. Поэтому в ТАУ используются специальные критерии устойчивости, позволяющие, в частности, избежать нахождение корней характеристического уравнения. Так называемые алгебраические критерии устойчивости основаны на известной связи коэффициентов характеристического уравнения

,a₀ > 0 (3) с его корнями  _i , i = 1,…,n.

1. Необходимое условие устойчивости линейной САУ, которое формулируется следующим образом:

для устойчивости линейной системы необходимо, но не достаточно, чтобы все коэффициенты характеристического уравнения (3) были строго положительны, то есть .

2. Необходимый и достаточный критерий устойчивости Гурвица, который формулируется следующим образом: линейная САУ будет устойчивой, то есть корни ее характеристического уравнения (3) будут иметь отрицательные вещественные части, если строго положительны определитель Гурвица (_n  0) и все его диагональные миноры (_i  0, i = 1,…, n-1).

Определитель Гурвица n-го порядка составляется по следующему правилу:

1) по главной диагонали от левого верхнего угла до правого нижнего располагаются коэффициенты уравнения (3), начиная с a₁ до a_n

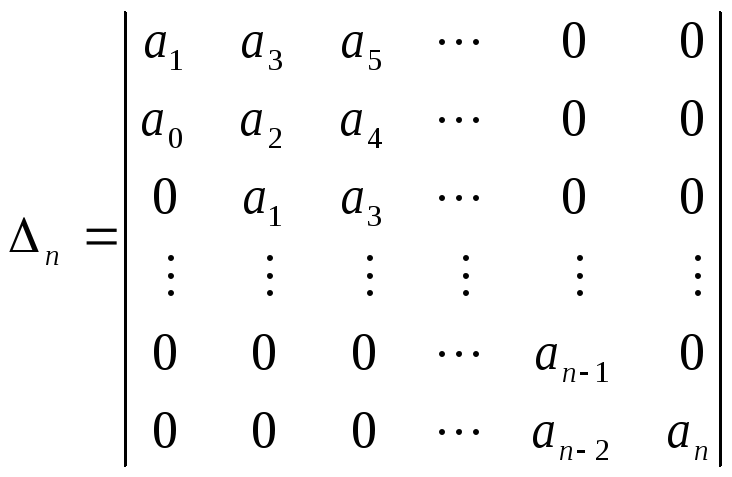; (4)

2) заполняются столбцы определителя. Каждый столбец дополняется вверх от диагонали последовательно коэффициентами с возрастающим индексом, а вниз – коэффициентами с убывающим индексом. В случае отсутствия такого коэффициента (то есть индекс меньше нуля или больше n) на его месте пишется нуль.

Диагональные миноры получаются отчёркиванием сверху слева по одной строке и одному столбцу, по две строки и двум столбцам и т.д.

42.ПОКАЖИТЕ,КАКИМ ОБРАЗОМ У СТАТИЧЕСКОЙ СИСТЕМЫ АВТОМАТИЧЕСКОГО РЕГУЛИРОВАНИЯ СТАТИЧЕСКАЯ ОШИБКА МОЖЕТ МОЖЕТ БЫТЬ СДЕЛАНА СКОЛЬ УГОДНО МАЛОЙ И КАКИЕ УГОДНОГО МАЛОЙ И КАКОЕ У ДАННОГО СПОСОБА ПРИ ПРАКТИЧЕСКОМ ПРИМЕНЕНИИ.

1. Определение понятие статической ошибки по функциональной схеме замкнутой системы.

регулятор

обьект

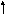
Где y*(t)- задающий сигнал,(t)-y*(t)-y(t)- ошибка,y(t)-выходной сигнал=

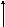
y*=y

T

2.Определение величины для системы автоматического регулирования углом тангажа структурная схема

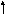
Wk(S)

Wпр(S)

Wп(S)

U(S)

Изобразим по Лапласу сигналов -задающий сигнал;- сигнал ошибки;- командный сигнал на привод органа управления,- сигнал отклонения ОУ;- выходной сигнал угла тангажа. ПФ-ПФ корректирующего устройства,- ПФ привода с ОУ. (U(S)=) пологая что,получаемKu)

- ПФ ЛА в угловом движении по тангажу.

Приведем данную структурную систему к типовому виду

- ПФ системы в развернутом состоянии, т.е при

Найдем ПФ системы в замкнутом соединении, т.е. когда есть главная обратная связь и

- ПФ для выходного сигналапо входу

- ПФ для ошибкипо входу

Найдем величину ,задавая- типовой ступенчатый сигнал, по теории операционного исчисления для конечного значения запишем

=

Таким образом увеличивая , можно уменьшить,т.к значения дляKиKокругляются конструктивными параметрами соответственно привода ЛА, то изменять в больших пределах можно коэф-тK, у корректирующего устройства.

2.Определим диапазон возможного изменения K. Рассмотрим характеристическое уравнение замкнутой системы, которое получаем по знаменателю Ф(S).Т.к для характ-ого уравнения 2-го порядка необходимо условие устойчивости,является также достаточными, то из требованиятаким образом теоретически диапазон изменения:, т.е. при

3.Ограничение на большие значения , рассмотрим по влиянию увеличения,на вид ЛАХ разомкнутой системы. Найдем ЧПФ,

Физический смысл - отношение амплитуды выходных колебании к амплитуде входных на заданной частоте.-сдвиг фаз колебании на выходе по отношению к входным колебаниям( при <0 , запаздывание). График ЛАХ, т.е в виде отрезков прямых асимптот, имеет в нашем случае следующий вид (удобно строить с использованием формального правила по)

L()

60

40

20

`

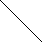1 10lg()

-20

-40

- частота сопряжения асимптот,-частота, при которой,т.е

Сигналы с частотой 0<< , усиливаются по амплитуде, а с частотойослабляются на выходе. Таким образомопределяет полосу пропускания. Таким образом, если увеличитьK,то график ЛАХ подымится, что приведет к увеличению частоты среза () т.е к увеличению полосы пропускания частот. Это значит вместе с полезными низкочастотными сигналами, будет без ослабления проходить высокочастотные помехи, ухудшая качество системы.

43.СФОРМУЛИРУЙТЕ С ПРИВЕДЕНИЕМ ОБОСНОВАНИЙ,КАКИЕ ТРЕБОВАНИЯ ПРЕДЪЯВЛЯЕТ САУ УГЛОМ ТАНГАЖА К ДИНАМИЧЕСКИМ,ВКЮЧАЯ ЧАСТОТНЫЕ,ХАР-М СЛЕДЯЩЕЙ СИСТЕМЫ, КОТОРОЙ ЯВЛЯЕТСЯ РУЛЕВОЙ ПРИВОД С ОРГАНОМ УПРАВЛЕНИЯ ПОЛЕТОМ,И КАКИЕ ТРЕБОВАНИЯ МОГУТ БЫТЬ ОБЕСПЕЧЕНЫ ПРИ ПРОЕКТИРОВАНИИ СЛЕДЯЩЕЙ СИСТЕМЫ.

CАУ угловым движением по тангажу: вход-угол отклонения управления органом полета(с помощью исполнительного устр-ва-привода)

выхлд-угол тагажа

Рассмотрим функциональную схему(какие элементы и как они взаимодействуют)

КУ-коррект.устр-во

Нарисуем структурную схему( ПФ и изображение сигналов)

Линеаризованные уравнения:

углового движения ЛА

исполнительного устройства (ИУ)

Запишем зад. урав. в операт. форме: ;.

ПФ ЛА в угловом движении по тангажу:

-коэффициент затухания :>=1-апериодическое звено (без колебаний), 0 << 1, то ПФW(s), описывающая угловое движение ЛА, представляет собой неустойчивое колебательное звено.

Т-постоянная времени [c] ----tпп<=3T

входной сигнал

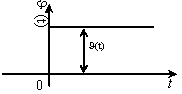
выходной сигнал

S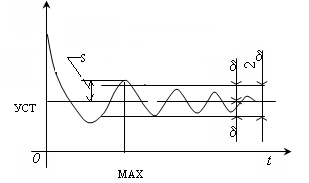-перерегулирование

Колебания => наличие комплексных корней характеристич. ур-я

tпп=2s, стремимся уменьшить Тстепень уменьшения амплитуды

Для устойчивости-корректирующее звено. знаменатель приравниваем к 0

Введем ПФ для привода ,,

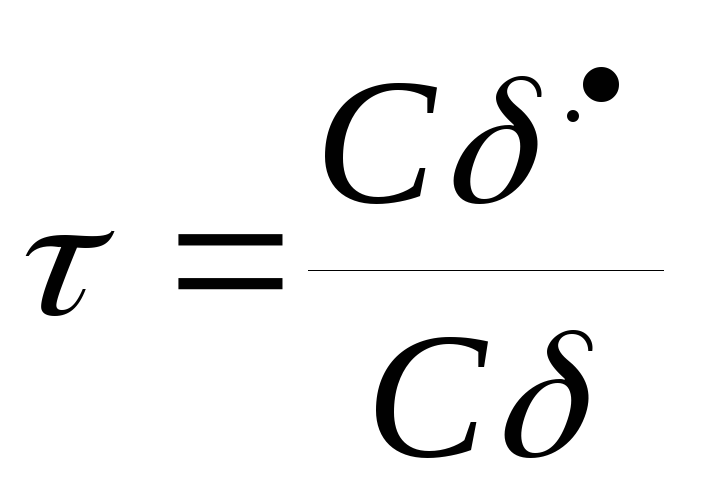ПФ корректирующего устройства (К1 –легко регулируется-электрические цепи => меняем сопротивление)

Требования к параметрам Кu и

Приведем структурную схему к типовому виду

Передаточная функция САУ в разомкнутом состоянии ()

Передаточная функция САУ в замкнутом состоянии ()

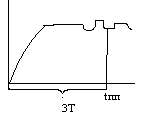
t<=T

Рассмотрим частотную ПФ

,-алгебраическая форма записи гдеU(t) =ReW(j) –вещественная частотная характеристика(ВЧХ);V(t) =ImW(j) –мнимая частотная характеристика(МЧХ).

- показательная форма записи,

– модуль ЧПФ;

– аргумент ЧПФ,

– отношение амплитуд вых и вх сигналов,-амплитудной частотной характеристикой

() – сдвиг фаз колебаний вых. и вх. сигналов,-фазовой частотной характеристикой(ФЧХ).

Для построения логарифмических частотных характеристик используется показательная форма ЧПФ Зависимость L() = 20lgAназываетсялогарифмической амплитудой частотной характер.Зависимость=() называетсялогарифмической фазовой частотной характеристикой(ЛФЧХ).

.

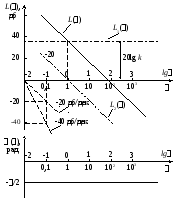0₁- области низких частот;

 ₁- область высоких частот, где- частотасопряжениянизкочастотной и высокочастотной областей.

Диапазон частот 0 _сопределяет, так называемую,полосу пропусканиячастот, так как в этом диапазоне сигнал передается системой без ослабления по амплитуде. Когда вся ЛАХ располагается ниже оси частот (приk1), то полосой пропускания считается диапазон (0₁) до наименьшей частоты сопряжения, то есть область низких частот.