3.Управление дальностью полета. По Бульбовичу:

1. V-скорость, Р - тяга.

2.

- потери связанные с дальностью, если они =0 то происходит отсечка тяги.

22. Возмущенное движение ла. Линеаризация уравнений возмущенного движения. Разложение возмущеного движения на продольное и боковое. Динамические коэффициенты.

Для линеаризации уравнений движения ЛА все кинематические параметры движения представляют в виде суммы их значений в невозмущенном движении и отклонений этих параметров от невозмущенных значений:

Индексом «*» обозначаются значения кинематических параметров в невозмущенном движении (при линеаризации считаем, что они являются известными функциями времени).- представляющие собой разности между кинематическими параметрами в возмущенном и невозмущенном движениях.

Продольное:

Боковое:

В отличие от разделения общего движения ЛА на продольное и боковое, когда боковое движение может существовать лишь на фоне вполне определенного продольного движения, возмущенное продольное и боковое движения могут существовать самостоятельно (система не имеет перекрестных связей).

Продольное движение ЛА.

Для упрощения связи вводят динамические коэффициенты a_ij.i– номер уравнения;j– номер эффекта, при котором… Нумерация динамических коэффициентов проводится в соответствии с таблицей:

0	1	2	3	4	5
V			y’		XB, YB, MZB

;

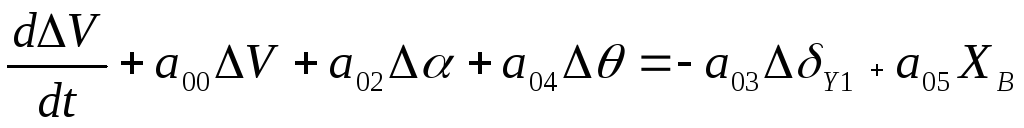
Система включает 4 уравнения, т. к. уравнение, описывающее вариацию , может быть проинтегрировано отдельно. Уравнение, описывающее вариацию, может не рассматриваться в соответствии с допущением при линеаризации. 4 уравнение может быть сразу учтено в 3. Данная система является не однородной. Для того, чтобы замкнуть систему необходимо ввести уравнение, описывающее работу системы управления. Частное решение этой системы:

,,,

Динамические коэффициенты (ДК):,,,,,,,,,,,,,,,,

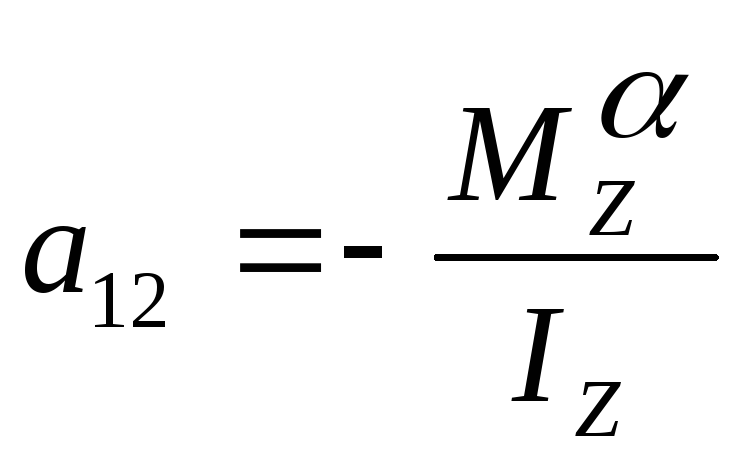ДК определяются массово-инерционными, энергетическими, аэродинамическими и геометрическими характеристиками ЛА, а также параметрами движения по невозмущенной траектории. Они характеризуют важнейшие динамические свойства ЛА, например, а₁₂характеризует продольную статическую устойчивость ЛА; а₁₁– демпфирующие свойства ЛА; а₁₃– эффективность органов управления. Т. к. ДК зависят от кинетических параметров движения по невозмущенной траектории, они являются функцией времени. По сути дела имеем линеаризованную систему уравнения… Общего аппарата исследования таких систем не существует. В этом случае целесообразно использовать прием замораживания коэффициентов.

Р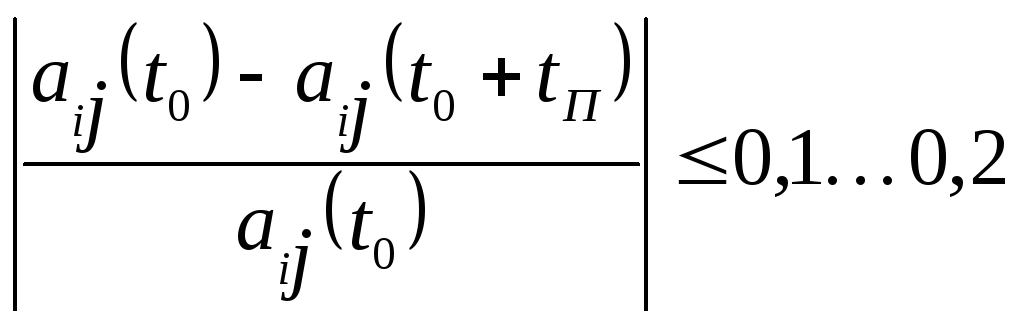асчетные точки – точки с экстремальными значениями кинетических параметров и динамических коэффициентов. (q_max,q_min; Н_потр; т. до выключения двигателя и после выключения; Н_min,H_max)

25. Классификация динам. Нагрузок, действующих на ла на различных этапах его эксплуатации. Нагрузка при транспортировке. Ветровая нагрузка. Акустическая нагрузка. Пульсация давления в камере рдтт.

Следует сказать, что термин “динамика” понятие достаточно широкое. Динамика– раздел механики, в котором изучается движение тел под действием приложенных сил.Динамическая нагрузка– нагрузка, для которой характерно быстрое изменение во времени, её значение и направления. Вызывает в элементах конструкции значительные силы инерции. Нагрузка претерпевающая изменение в течении времени, не превышающего 2-3 периода свободных колебаний конструкции.Нестационарная аэродинамическая нагрузка– обусловлена турбулентностью продуктов сгорания (ПС), неустойчивым взаимодействием УВ с ПС, срывами потока. Особенно характерна для трансзвуковых режимов. Вызывает вибрацию и влияет обычно на местную прочность конструкции корпуса ЛА.

Рассматривая этапы эксплуатации ЛА можно выделить следующие динамические нагрузки: 1.Статические; 2.Динамические. Характерно, что одна и та же нагрузка может рассматриваться и как статическая и как динамическая. То есть одна и та же нагрузка для одной конструкции 6быть статической, а для другой динамической.

Нагрузка при транспортировке

Наблюдается при транспортировке ракет всеми видами транспорта (морским, воздушным, ж/д, автомобильным). Для такой нагрузки характерны вибрации и толчки, носящие случайный характер. Значение инерционных сил определяется видом используемого транспорта, конструкцией экипажа и режимом транспортировки. В результате действия сил зависящих от: -Массы тележки (её распределение по длине и ширине); -Жёсткости рессор и балансировки колёс; -Числа колёс и их расположение относительно центра тяжести; -Неровности дороги; -Жёсткости дорожного покрытия; -Скорости движения. Например твёрдо топливный заряд получает некоторую величину накопленных повреждений. Движение транспортной тележки по дорожному профилю рассматриваем как стационарный случайный процесс, т.е. процесс не зависящий от начала отсчёта времени.

На различных участках дороги имеются неровности самой разнообразной формы и размеров. В чередовании неровностей нельзя установить какой либо определённой закономерности, следовательно и спектр возмущений на тележку носит случайный характер, и амплитуды колебаний тележки с ракетой будут случайными величинами. Для использования детерминированного подхода (инженерной практики) устанавливают наиболее часто встречающиеся неровности, принимаемые как типичные.

Общие характеристики дороги в этом случае выражаются значением математического ожидания, дисперсией (средним квадратичным) высоты неровностей. Для ж/д наиболее наиболее интенсивные вибрации (амплитуда перегрузок 0.5-1)при частотах 2-8 Гц наблюдаются в вертикальном и продольном направлениях. Детерминированный подход есть упрощение. Наиболее часто это упрощение сводиться к изолированному рассмотрений упругих колебаний ЛА и упругих колебаний транспортного средства с абсолютно жёстким ЛА. Чем меньше вес ЛА по сравнению с весом тележки, тем влияния ЛА на динамические характеристики системы в целом, и тем оправдание такой подход.

Ветровая нагрузка

Отклонение действующих значений параметров атмосферы от стандартной учитывается путём введения дополнительных аэродинамических нагрузок (возмущающих сил). Возмущением является и ветер. Приближённо его влияние оценивается изменением углов атаки и скольжения ; , гдеисоставляющие скорости ветра и изменением скоростного напора..

Величина скорости ветра зависит от географической широты, места старта, времени года, суток, а в основном от h.Наряду с установившемся течением существуют вихревые (небольшой протяжённости), но со сравнительно большими скоростями, которые получили названиепорыв ветра.

Атмосферные турбулентности требуют изучения (кучево-дождевые облака). В настоящее время установлено: порывы ветра одинаковой интенсивности равновероятны в любом направлении (горизонтальном, вертикальном).

Наиболее распространено следующее описание формы порыва:

, гдем/с,м.

Порывы изучаются опосредованно обработкой результатов полёта самолётов. Для ракет менее изучены.

Акустическая нагрузка

На границе газовой струи, истекающей из сопла со сверхзвуковой скоростью, обычно образуется зона турбулентного потока, которая генерирует окружающее пространство звуковые волны различной частоты. Толщина этой турбулентной зоны непрерывно увеличивается по мере удаления от среза сопла. Меняется и спектр частот. Вблизи сопла находятся источники высокочастотных звуковых волн, а в области струи с полностью развитой турбулентностью – источники в основном низкочастотных звуковых волн. В области смешения, в которой поток остаётся сверх звуковым, возможно генерирование дополнительных пульсаций давления, обусловленное взаимодействием ударных волн с турбулентностью. Интенсивность шума, создаваемое струёй, пропорционально её средней скорости в степени , а акустическая мощность составляет ()% от механической мощности ДУ. То есть с увеличением пропорционально увеличивается нагрузка на поверхности конструкции (дб;гдеПа). Воздействие таких нагрузок оказывает существенное влияние на режимы вибрации элементов конструкции ЛА, на функционирование приборов, на усталостную долговечность частей ЛА. Моделирование для определения частоты пульсации:

, где- выходной параметр сопла,- частота в Гц,- средняя скорость струи.

Пиковые значения давления в период запуска могут в несколько раз превышать установившееся давление. С ростом скорости полёта суммарный уровень звукового давления падает и при звуковые волны, звуковые волны генерирующие со сверхзвуковой струёй, не достигают частей корпуса ЛА, расположенных впереди двигателя.

Пульсация давления

Пульсации вызваны неустойчивостью, а точнее автоколебательность внутри камерных процессов (ЖРД, РДТТ). Неустойчивость снижает надёжность, увеличивает сроки отработки вследствие чего увеличивается стоимость изделия, может вывести из строя бортовую аппаратуру, разрушить двигатель и ЛА. Различают низкочастотныеивысокочастотныеколебания в камере сгорания РДТТ. Низкочастотные неустойчивые колебания определяются автоколебаниями в камере сгорания с частотой, меньшей, чем минимальная собственная акустическая частота (объёмные колебания,Гц). При высокочастотных неустойчивых колебаниях в камере сгорания распространяются акустические волны (продольные и поперечные (тангенциальные, радиальные и смешенные)). С поперечными колебаниями в РДТТ борются посредством добавления металла.

В последнее время остро стала проблема продольной акустической неустойчивости.

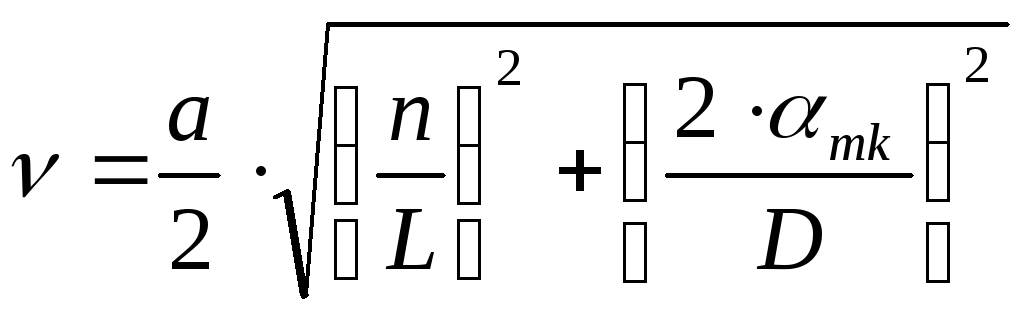, (Гц), где- скорость звука;L, D– длина и диаметр канала заряда;n– целое число;-k-ый корень уравнения. Следует обратить внимание, чтоm– соответствует тангенциальным колебаниям;k - радиальные колебания., где- функция Бесселя 1-го рода порядкаm;m – целое число;- аргумент функции Бесселя.

26.ПРОДОЛЬНЫЕ КОЛЕБАНИЯ КОРПУСА РАКЕТЫ. МЕТОД ПОСЛЕДОВАТЕЛЬНЫЙ ПРИБЛИЖЕНИЙ ПРИ ОПРЕДЕЛЕНИИ СОБСТВЕННЫХ ЧАСТОТ И ФОРМ КОЛЕБАНИЙ. ВЫНУЖДЕННЫЕ ПРОДОЛЬНЫЕ КОЛЕБАНИЯ КОРПУСА РАКЕТЫ ПРИ ВЫКЛЮЧЕНИИ ДВИГАТЕЛЯ. МАСКИМАЛЬНОЕ ПРОДОЛЬНАЯ РАСТЯГИВАЮЩАЯ НАГРУЗКА ДЛЯ СТЫКОВЫХ СОЕДИНЕНИЙ.

Продольные колебания корпуса ракеты. Метод последовательных приближений при определении собственных частот и форм колебаний. Вынужденные продольные колебания корпуса ракеты при выключении двигателя. Максимальная продольная растягивающая нагрузка для стыковочных соединений.

Продольные колебания

При продольных колебаниях в поперечных сечениях корпуса возникают напряжения растяжения и сжатия. Простейшей схемой жидкостной ракеты (которую будем считать осесимметричной) при определении форм и частот продольных колебаний может служить прямой неоднородный стержень. Схему неоднородного стержня для приближенного расчета можно принять только в том случае, когда перемещение жидкого топлива относительно стенок бака при продоль­ных колебаниях мало и его можно не учитывать.

У большинства жидкостных ракет и, в первую очередь, у крупных ракет-носителей с насосной системой подачи топлива стенки баков сравнительно тонкие. При продольных колебаниях прогибы дна и раздутие обечаек баков значительны, вследствие чего значительны и перемещения жидкости относительно стенок баков в направлении оси ракеты. Расчет упругих продольных колебаний корпусов таких ракет нужно проводить с учетом деформаций дна и радиальных деформаций обечаек баков.

Одну из возможных динамических схем можно представить в виде пружинно-массовой модели.

Пружинно-массовая модель дает удовлетворительные ре­зультаты при расчете форм и частот свободных колебаний низших тонов.

Д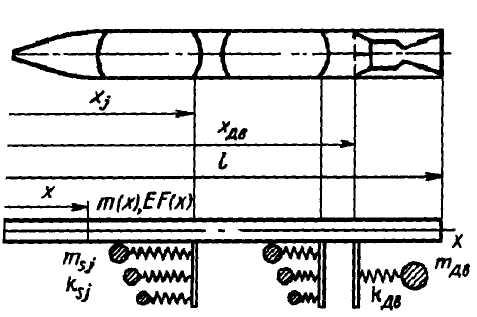ля более полного учета колебаний жидкости в баках и распределения массы и жест­кости по длине можно реко­мендовать схему прямого не­однородного стержня с упруго подвешенными грузами (меха­ническими осцилляторами). Колебания каждого осциллято­ра являются механическим аналогом соответствующего тона осесимметричных колеба­ний жидкости в упругом баке. Сумма масс всех осцилляторов равна массе жидкости в баке, частота свободных колебаний одного осциллятора равна частоте свободных колебаний соответствующего тона жид­кости в упругом баке.

За точку приведения прини­мается центр упругого дна бака, поэтому перемещение масс осциллятора при колебаниях относительно жесткого дна будет характеризовать перемещение центра упругого дна бака относительно силового шпангоута. Такой выбор точки приведения упрощает сопряжение колебаний дна бака с колебаниями топлива в трубах.

Так как двигатель и турбонасосный агрегат (ТНА) подвешиваются к корпусу на раме, представляющей собой упругую конструкцию, то при продольных колебаниях перемещения двигателя и ТНА относительно корпуса можно заменить перемещением сосредоточенной массы на пружине.

ТНА, подвешенный на раме отдельно от двигателя, при продольных колебаниях корпуса ракеты можно рассматривать так же, как сосредоточенную массу на пружине. В обоих случаях к массе ТНА следует прибавлять массу столба жидкости, заключенную в трубопроводах (между ТНА и свободной поверхностью в баках).

В практических расчетах форм и частот низших тонов колебаний корпуса достаточно учитывать лишь несколько первых тонов колебаний жидкости в баке, поэтому число осцилляторов может быть небольшим (2-3). Пружины остальных осцилляторов можно считать жесткими, а подвешенные на них сосредоточенные массы - присоединенными к массе силового шпангоута бака.

Для определения форм и частот собственных продольных колебаний корпуса ракеты принимается схема прямого неоднородного стержня с упругоподвешенными сосредоточенными массами.

Уравнение колебаний неоднородного стержня будет иметь следующий вид:

(1)

Уравнение (1) для собственных колебаний будет иметь следующий вид:

(2)

Рассмотрим уравнение (3) в виде n-го тона смещения:

(3)

Подставляя уравнение (3) в уравнение (2), получим уравнение продольных колебаний стержня, которое определяет тон собственных форм колебаний:

(4)

Решение данного уравнения будет зависеть от ГУ: пусть начало координат находится на одном их концов ракеты, тогда граничными условиями будут отсутствия перемещений на концах ЛА.

Решение (3) и (4) с учётом граничных условий позволит определить собственные частоты для стержня. Используя метод последовательных приближений можно с любой точностью определить эти частоты.

Следующий шаг в методе последовательных приближений:

Разбиваем ракету на участки. Будем считать, что каждый участок имеет постоянную жёсткость и равномерное распределение массы. Граничные условия будут определяться моделью стержня со свободными концами.

Дифференциальное уравнение свободных продольных колебаний любого i-го участка будет иметь постоянные коэффициенты:

(5)

Для вынужденных продольных колебаний:

1. Определяют собственные колебания методом последовательных приближений для случая стержня.

2. Определяют частоты и амплитуды первого и второго тона.

3. Сравнивая частоты собственных колебаний с частотами вынуждающих сил, определяем коэффициент динамичности:

Данный коэффициент позволяет определить нагрузку, которую испытывает соединение от действия вынуждающей силы.

Метод последовательных приближений позволяет определять формы и частоты собственных колебаний с любой степенью точности. Особенно эффективен этот метод при определении низшей частоты колебаний.

Рассмотрим порядок расчета на примере системы с диагональной матрицей масс.

Задают приближенно форму колебания u_i⁽⁰⁾ (нулевое приближе­ние).

Определяют силы инерции при амплитудных отклонениях системы:

(значение частоты p⁽⁰⁾может быть произвольным).

3. Методами строительной механики определяются перемещения u_i⁽¹⁾, вызванные силами F_i. Значения u_i⁽¹⁾ представляют собой первое приб­лижение к форме собственных колебаний.

4.Находят первое приближение для частоты собственных колебаний, например, по формуле Рэлея:

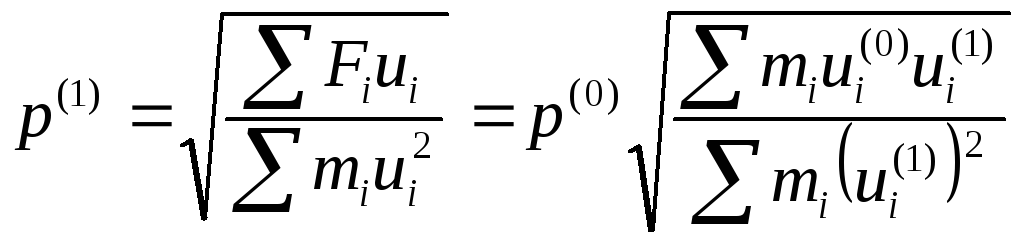
Далее за исходную принимают форму первого приближения и проводят повторный расчет, в результате которого определяют второе приближение, и т. д. Частоты при последующих приближениях опре­деляют по формуле

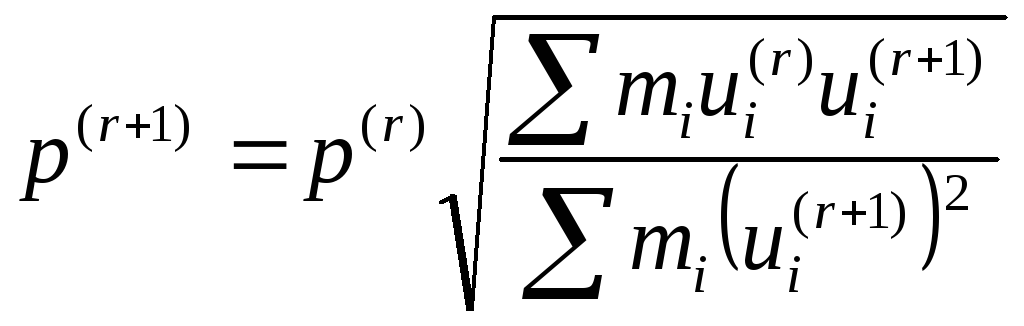
Свидетельством того, что процесс последовательных приближений сошелся, является пропорциональность смещений при r-м и (r+1)-м приближениях, т. е. независимость отношения от номераi.

Заметим, что если это условие соблюдается, то формула для расчета частоты может быть упрощена:

причем отношение берется в одной из точек системы.

Формулой следует пользоваться при расчете частоты, когда форма существенно отличается от формы (например, при первом приближении), формулой — при последующих этапах приближений.

27.ПЕРЕДАТОЧНАЯ ФУНКЦИЯ УПРГОГО ЛА ПО УГЛУ ТАНГАЖА. ВЫБОР ОПТИМАЛЬНОГО МЕСТА УСТАНОВКИ ПРИБОРОВ СИСТЕМЫ УПРАВЛЕНИЯ. ПАРАМЕТРЫ, ОПРЕДЕЛЯЕМЫЕ ПРИ ДИНАМИЧЕСКИХ ИСПЫТАНИЯХ РАКЕТ. ВЛИЯНИЕ ДИНАМИЧЕСКИХ НАГРУЗОК НА НАДЕЖНОСТЬ РАКЕТ.

Передаточная функция ЛА с учётом его упругости:

Передаточная функция ЛА – та реакция, которую конструкция ЛА оказывает на внешнее воздействие, преобразуя их в колебания его элементов или формализуя в управляющее воздействие.

В области высоких частот, порядка нескольких десятков герц, необходимо учитывать упругость корпуса, так как возможно возникновение резонансных режимов работы, когда частоты колебания рулей органов управления будут близки к частоте собственных колебаний самого корпуса. Таким образом, частотные характеристики «абсолютно жёсткого» ЛА не будут соответствовать действительности.

Рассмотрим модель изгибных колебаний балки с учётом её упругости:

(1)

Сущ. влияние на упругие колебания оказывает а/д силы (возможно и возникновение флаттера – газоупругого взаимодействия конструкции с набегающим потоком). В данном случае испол. модель упругой балки со свободными концами. Граничные и начальные условия для данной модели: - изгибающий момент: ; - перерезывающая сила:

Для нахождения передаточной функции решаем уравнение (1) в преобразованиях Лапласа:

(2), где

Данное решение будет состоять из двух частей: решения однородного и неоднородного уравнений. Решение однородного будет заключаться в поиске всех гармоник колебаний и функции прогиба, и будет являться передаточной функцией абсолютно жёсткого ЛА. Данное общее решение будет удовлетворять граничным условиям, но не будет удовлетворять начальным условиям.

Для того, чтобы найти решение неоднородного уравнения необходимо в общем решении найти постоянные коэффициенты. Решение найденное таким образом будет удовлетворять и начальным и граничным условиям.

Полная передаточная функция по углу тангажа (аналогично можно найти передаточную функцию и для углов крена и рыскания) будет иметь вид:

Эта передаточная функция связывает угол отклонения управляющего органа, в данном случае руля высоты, с углом, измеряемым при помощи свободного гироскопа.

Выбор оптимального места установки приборов системы управления:в ц.м. ЛА.

П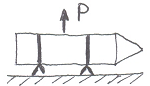араметры, определяемые при динамических испытаниях ракет: Проводятся с целью определения собственных частотных хар-к.

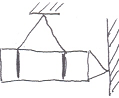
1) Импульсные (P): проводятся в стапеле.

2) для продольных колебаний: В отсеки устанавливаются пирапатроныточечное воздействиеволна.

3) Крутильные: величина определяется в течение 15-ти минут.

Измеряются собственные частоты прогиба, продольных и крутильных колебаний.

Определяется коэф-т демфирования – отношение амплитуд через период: .

Определяются maxнапряжения и зоны их напряжения. Особое внимание указывается на стыковочные узлы, геометрию сечения ЛА.

Влияние динамических нагрузок на надежность ракет: основная задача найти коэффициент динамичности.

28.ДИНАМИЧЕСКОЕ ПОВЕДЕНИЕ ЗАРЯДА, СКРЕПЛЕННОГО С КОРПУСОМ РАКЕТЫ В ПРОЦЕССЕ ТРАНСПОРТИРОВКИ(УТОЧНЕННОЕ РЕШЕНИЕ). УЧЕТ ДИНАМИЧЕСКИХ СВОЙСТВ ТВЕРДОГО РАКЕТНОГО ТОПЛИВА. ОТЛИЧИЯ В РЕШЕНИИ ОТ БАЛОЧНОЙ ПОСТАНОВКИ ЗАДАЧИ.

Динамическое поведение заряда скрепленного с корпусом в процессе транспортировки.

Решение данной задачи полагается с допущениями.

- материал корпуса и заряда изотропны постоянны.

- колебания будут линейно – упругими.

Характеристика, будет зависеть от частоты и температуры заряда.

Тогда основным расчетным случаем будет случай, когда значение действительных нагрузок максимальны, а свойства топлива – минимальны. Чем выше V=> вышеE.

Основа узлов, которая определяет изменение модуля.

(1)

V’ – частота нагружения.

а_T– коэффициент температуры смещения (показывает изменение физико-механических свойств на 1⁰).

– зависимость динамического модуля от скорости нагружения и температуры заряда с₀– определяет характеристику модуля при нормальных условиях (+20⁰).

Условия (1) необходимо учитывать при определения физико-механических свойств задачи, при этом коэффициент Пуассона для топлива 0,5. Решение уравнения колебаний заряда в цилиндрической системе координат запишем в следующем виде:

(x) продольные

(y) окружные(2)

(z) радиальные

- набла

Р – нагрузка

ρ – плотность

дифференциальный оператор Лапласа (3)

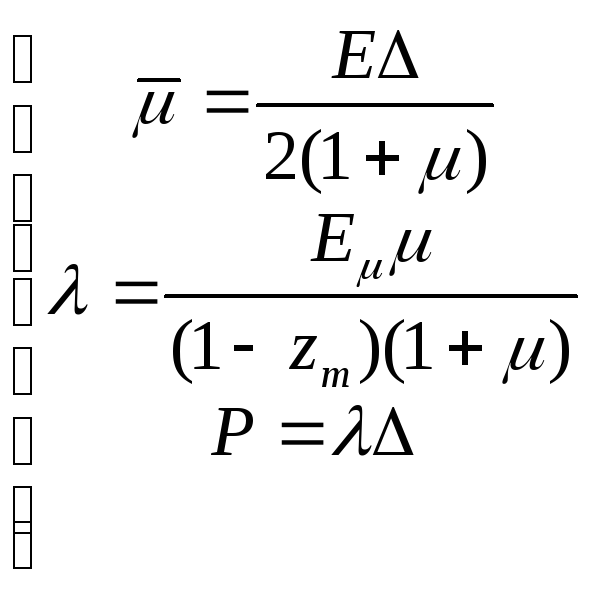- неопределенная функция нагрузки, которая возникает вследствие сечения при возникновении колебаний, то есть величина этой нагрузки будет связана с объемными напряжениями растяжения или сжатия при действии знакопеременной нагрузки

Условие (3) позволяет рассматривать систему уравнений (2) в аналитическом виде, тем самым позволяет определить НДС заряда при транспортировке при возникновении колебаний ракетного топлива.

Для определения частоты соответствующих колебаний необходимо рассмотреть систему уравнений (2) в результате чего найдены в общем виде колебания по r, по окружности изменения, отсюда следует что по деформациямv, υ,w, которые будут определять амплитуду колебаний на частоте, которая будет определять условия физико-механических свойств материала.

Для удовлетворения условий на границе необходимо рассмотреть изменения параметров в зоне контакта корпус-топливо, по торцам, в зоне канала для рассмотрения условий на границе зададимся, что давление в камере равно атмосферному, r_k– постоянно. Внутренняя нагрузка на корпус РДТТ отсутствует.

Для решения уравнения (3) надо записать начальные условия топливного заряда при условии его скрепления с корпусом.

Условие на торцах записывается для каждого конкретного вида закрепления торца:

манжета блокирует торец δ_zφ=0,τ_φ2=τ_zφP=0

условия прочного скрепления τ_{k т.к}=τ_{k к.т}δ_т.к= δ_к.т

данные условия позволяют решить (3) как некую функцию изменения давления и представить в виде ряда используя метод разложения Фурье по координатам в цилиндрической системе координат.

Давление запишем так:

P=P₁(r)P₂(r)P₃(φ)T(t) (4)

Позволяет получить бесконечное множество решений, которые будут характеризовать поведение топливного заряда при действии динамической нагрузки (Р). Подставив (4) в (3) получим для меридиональной состав

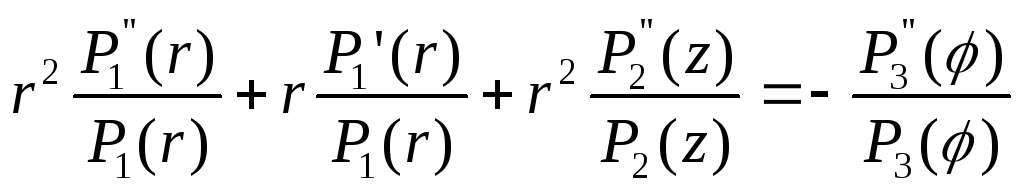(5)

Так же выражению изменение динамической нагрузки по rиz, так как используются ортогональные уравнения

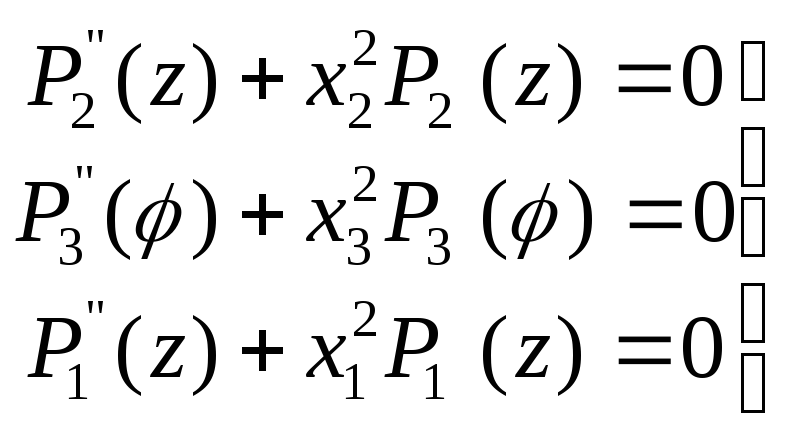(6)

т.е разделение системы уравнений, по нагрузке исходя из (5) позволяет получить уравнения. Это позволяет получить определенные характеристики, которые будут зависеть от выбранной системы координат и определять зависимость только от 1-го параметра.

Полное решение (3) с учетом динамического разложения Р (6) может быть решено с заменой дифференциальных составляющих уравнения с использованием функции Бесселя, которая позволяет дифференцировать форму представления заменить на алгебраическую, то есть привести к простому уравнению: (7)

Если учесть, что каждая составляющая будет определять формулу колебаний, то можно предположить, что если описывать ортогональности P=0, то для изгибных колебаний

x₃будет носить функцию определяющую моду колебаний при изгибе, то есть она может для собственных частот иметь целые значения.

Ограничим рассмотрение 3-я модами и для V-ой моды найдем велечину динамического давления в следующем виде(8)

(8) – будет определять значение динамического нагружения при собственных колебаниях топливного заряда при изгибе по I– ой моде этих колебаний.

Подставив значения динамического давления из (8) в уравнение по перемещению получим значение перемещений при этих колебаниях

C₁,C₃,C₄,C₅,C₆,B₁,φ₁– постоянные коэффициенты интегрирования, которые получены при рассмотрении граничных условий при решении системы уравнений (3). Функция Бесселя:

- φ₁k₁– модификация функции БесселяIIрода

- I₁–Iрода.

То есть рассматриваем и деформации по окружным и радиальным компонентам. То есть условия, которые определяют структуру НДС при динамическом нагружении топливного заряда, будут формализованы через колебательный процесс, который рассматривается для первых 3-х мод этих колебаний (так как здесь 98% энергии колебаний).

Моды

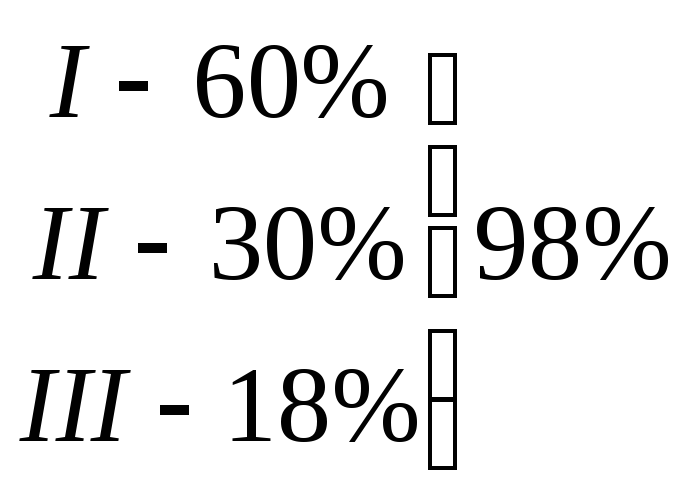
Под нагрузкой понимают массовые силы, действующие на заряд.

Наличие давления приводит УК изменению уровня НДС и используя принципы суперпозиции данную задачу рассматривают отдельно от колебаний, то есть изменение условий, которые позволяют решить данную систему (3) необходимо учесть значения напряжений и деформаций на границах заряда.

(10)

Это позволяет определить постоянные интегралов подставив значения деформации и напряжении в уравнения (8) и (7)

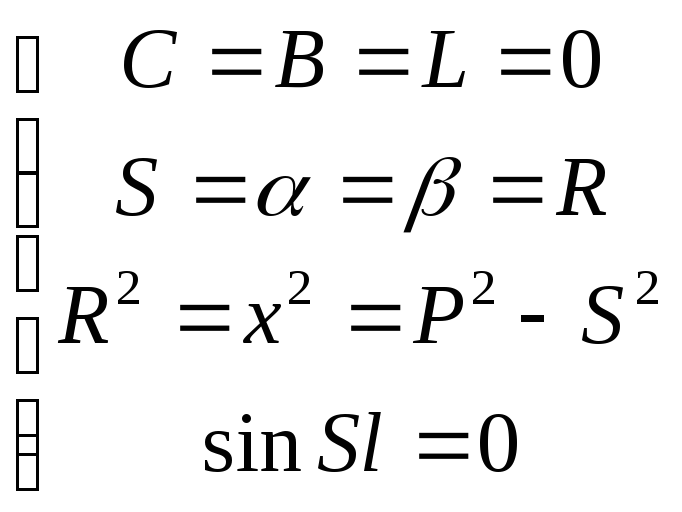(11)

Исходя из (11) переведя изгиб в форму колебаний

(12)

указывая форму моды колебаний можно получить уравнения для определения функции деформации в виде уравнений колебаний толстостенного оболочки (цилиндра).

Данные условия деформации будут иметь вид b=R,a=r

(13)

- коэффициент жесткости корпуса.

То система уравнений (13) позволяет определить изменения деформации топливного заряда при изгибных колебаниях оболочки.

R₁– параметр изгиба оболочки

Показывает maxвеличину относительно возможного изгиба оболочки. В результате расчета зависимостей системы равнений (13) из деформированной формы преобразовать в алгебраическую использую функцию Бесселя.

То есть (13) может быть реализованы в виде гармонической функции, где основные параметры определяются изгибными колебаниями будет частота. Частота свободных колебания будет определятся

(14)

Следовательно структура оценки динамического состояния топлива заряда при изгибных колебаниях сводиться к форме прогиба (13) при определении частоты свободных колебаний (14) при соответвующем определенным параметрам динамической нагрузки g_1,2,3как сил Р (7).

Для рассматриваемого аппарата позволяющего определить полную структуру НДС необходимо учитывать рассмотренную структуру как балочную, но и не более полную структуру зависимостей, которая будет определять δ горящего свода δ оболочки.

Незначительная погрешность будет при больших удлинениях заряда, а при коротких большая.

Если рассматриваемый топливный заряд происходит изменение формы, механизм такого поведения называется вязкими моделями.

Оценка зоны: необходимо рассматривать условие когда характер из перемещений диагональных зон канала будет соответствовать сжатию канала, то есть величина изменений радиуса канала будет определяться деформацией корпуса. Тогда в 1-ом приближении величина деформации осевых в заряде определяется из геометрических соотношений

;;

Будет вычислено при условии, что величина Wдеформации будет известна.

Тем не менее структура формы изменения канала будет определять, не сколько физико-механическими свойствами топлива, а жесткостью металла при колебаниях.

Для оценки НДС топливного заряда изменение динамической нагрузки необходимо учитывать не только изменение физико-механичеких свойств материала, но и условий (скоростных параметров) действующей нагрузки.

Транспортные нагрузки.

НДС скрепленного одним торцом.

Принимается:

характер нагружения близок к гармоническому;

поперечное сечение в процессе колебания остается плоским;

изгиб проходит в 1 плоскости.

Задача решается в упругой постановке без учета вязко-упругих свойств материалов. В окончательных результатах последнего учитывались в виде температурно-внешней (температурно-частотной) зависимости характеристик материала E(T,t), ε_кр(T,t), τ_кр(T,t).

Схема нагружения при кинематическом возмущении в заделке по закону: z=U₀cosωt

Уравнение поперечных колебаний имеет вид

(1)

Где z,x– координаты,t– время;

(2)

E– модуль упругости материала;

ρ – погонная плотность;

- момент инерции (3)

Граничные условия: z=U₀cosωt;x=0;x=l (4)

Решение уравнения (1) ищем в виде

(5)

Подставив (5) в (1) и сократив на множитель получим с одной переменой x

(6)

Решение каждого записывается (7)

Подстановка (7) и (6) получаем характеристическое уравнение

(8)

корни которого равны ,,,(9) где. Таким образом, решение уравнения (6) с учетом (9) примет вид:

им в более удобной форме(10)

Постоянные A,B,C,Dопределяются из граничных условий

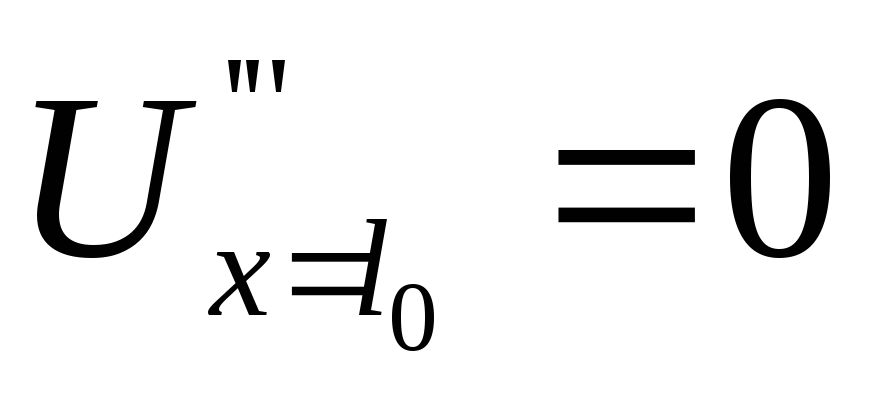,,,(4’)

Первый два условия дают

Из двух последующих условий получаем:

Решая их совместно по формулам Кламера получим

, , , (11)

Где (12)

Следовательно, решение уравнение (10) запишется в виде

(13) приимеет случай резонанса. Первые два корня характеристического уравнения

Равны соответственно ,

Следующие находятся из выражения ,i=1, 2, 3, … (14)

формула для резонансной частоты с учетом (9)

(15) известно, что напряжения при изгибе можно выразить через изгибающий моментаM_из

(16) где, формула (16) имеет вид

(17) Иногда в практике можно ограничиться двумя первыми членами ряда, тогда формула (17) преобразуется:

(19)

Со свободным торцом.

Уравнение равновесия для произвольного сечения цилиндра

(1)

U(x,t) 0 смещение сечений стержня вдоль осиx,t– время,x– координата.

(2)

скорость распространения упругой волны

Е – модуль материала,

S₀– площадь в перечном сечении,

l₀- длина цилиндра,

М – масса цилиндра.

Начальные условия:

; (3)

краевые условия:

(4) с помощью преобразования Лапласса (операционное исчисление) искать решениеU(x,t) является оригиналом по переменнойt.

, где- изображение оригинала.

Дифференцируя оригинал (1) будет

x– рассмотрим как параметр и по теореме дифференцируя по параметру получим

Подставив (1) получим

(5)

Краевые и начальные условия преобразуются

;

(6)

Общее решение запишется

,k₁иk₂находиться из условия (6)

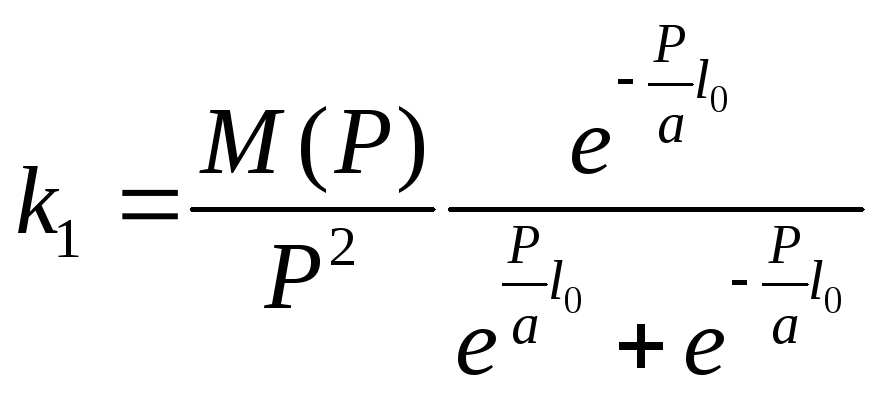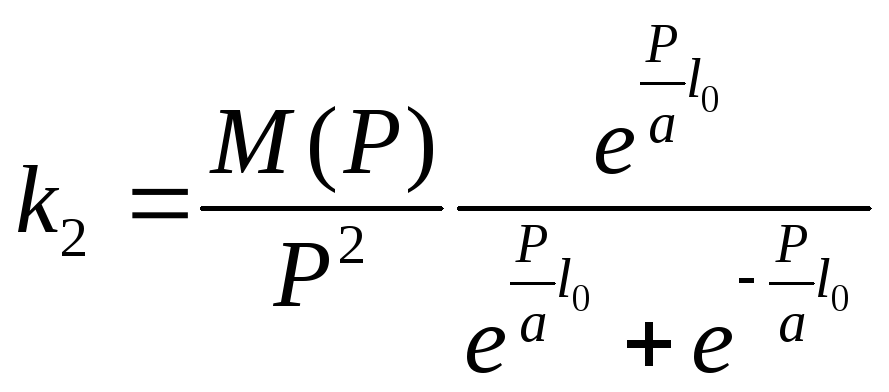,(7)

Произведение по x(деформации), зная которые легко найти напряжения в рассматриваемой точке сечения. Согласно теории о деформации по параметрам имеем

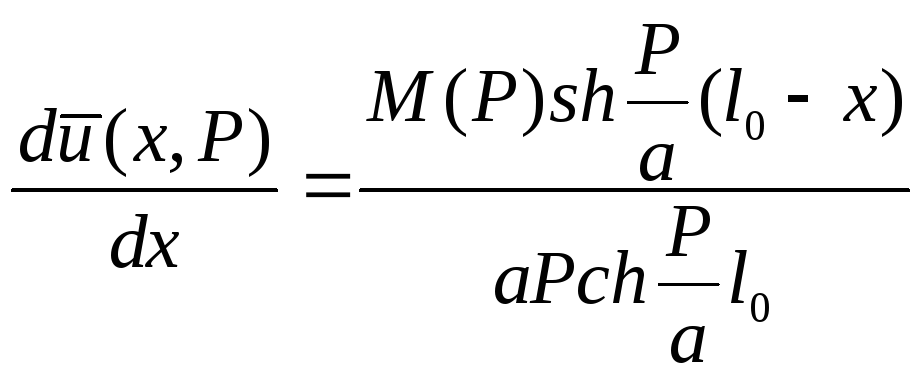(8)

Необходимо знать функцию М(Р) – для нахождения оригинала.

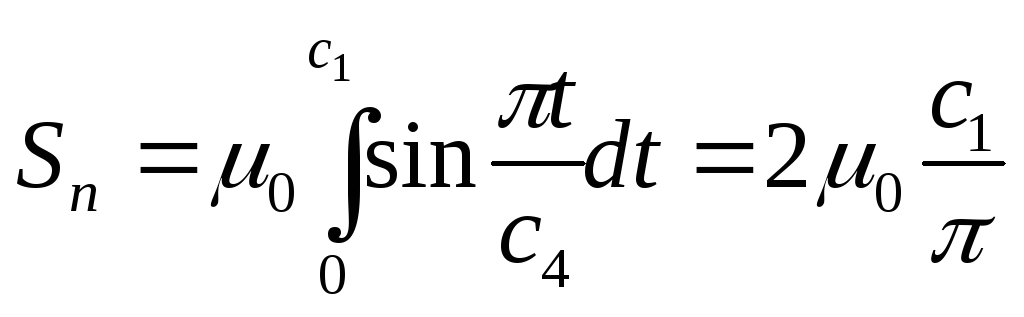
Из равенства площадей

,

Задаваясь с₃, с₄, с₂– определить можно с, с₁из условия равенства площадей.

Прямой импульс.

Отображение

,

тогда

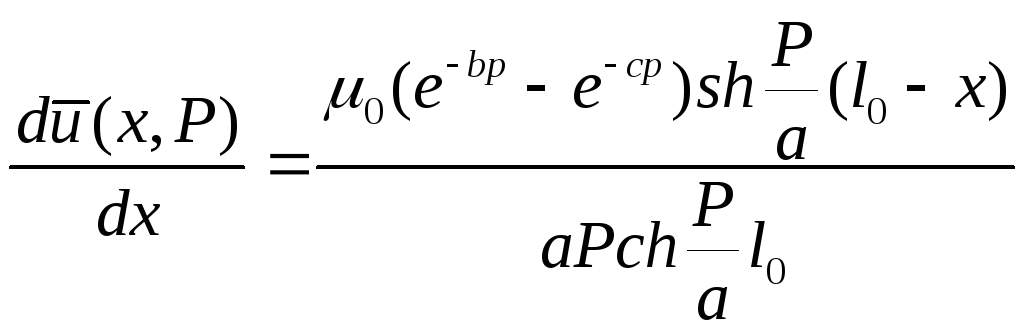
Оригинал соотношения (8) по теореме обращения

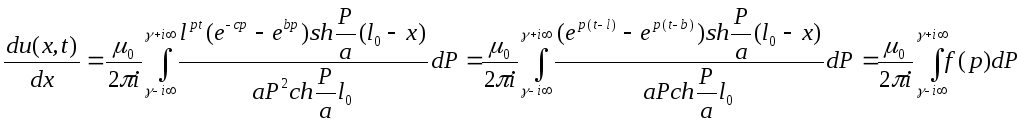
тоже вычисления интеграла (9) найти сумму вычетов функцииf(p). Она однозначна относительно Р и имеет полюс порядка при Р=0и простые полюса в точке, где

,n=0,1,2, … (10)

Вычеты для полюсов второго порядка в точке Р=0 находится по формуле

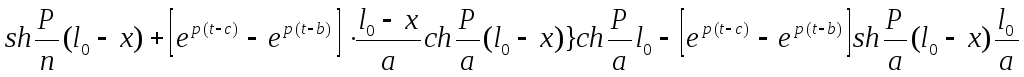
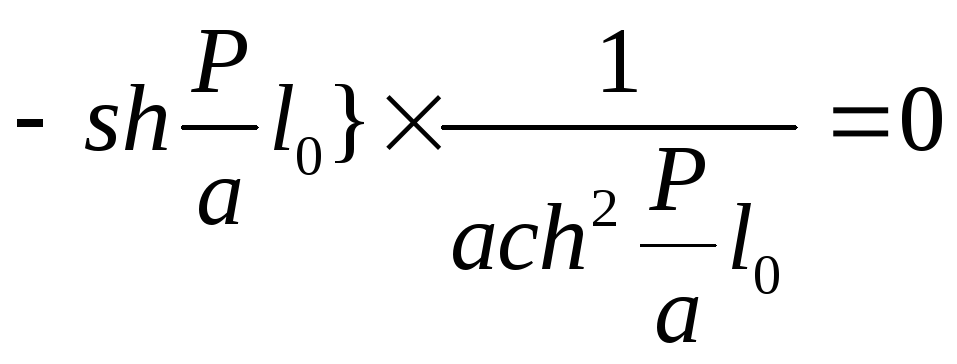(10)’

Вычеты относительно простых полюсов в точках находятся из условия, что функция, причемгде Р=а простой полюс, то вычет равен

(10)”

В рассматриваемом случае , тогда

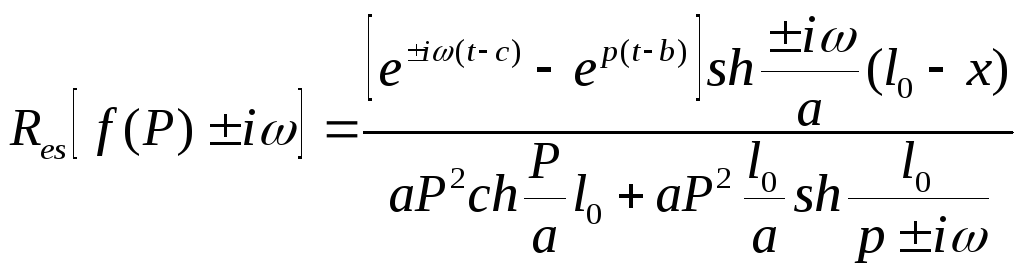
Принимая во внимание (10) и вычисляя гиперболические функции

Получим

(11)

Преобразуем выражение (11) через тригонометрическую функции и заменим для каждого знака

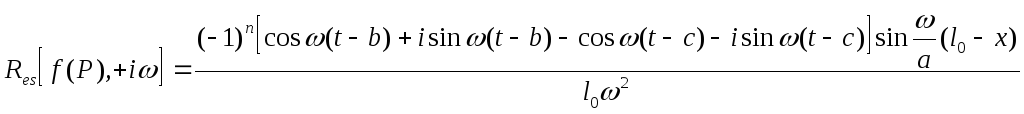
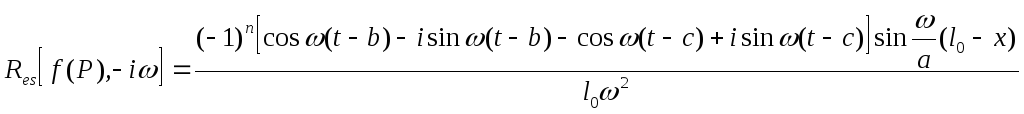
С учетом последних соотношений формула (11) примет вид

После преобразования в квадратных скобках имеем

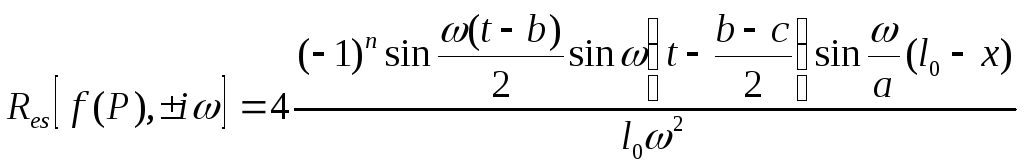(11)’

Найдены вычеты функции относительно всех полюсов. Соотношение (9) преобразуется к виду

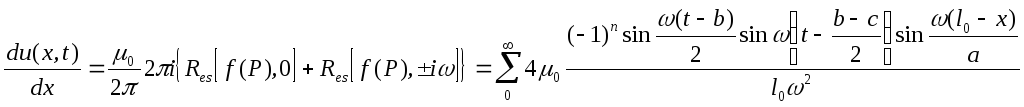(12)

Выражение получилось в виде бесконечного знакопеременного абсолютно сходящегося ряда (по признаку Даламбера)

Исследование: максимальное значение функции будет, когда

То есть при

(12)’

Принимая во внимание (10) из соотношения (12) следует, что максимум деформации будет в зоне контакта цилиндрического, то есть в сечении x=0 в момент времени

Выражение максимальных деформаций запишется:

(13)

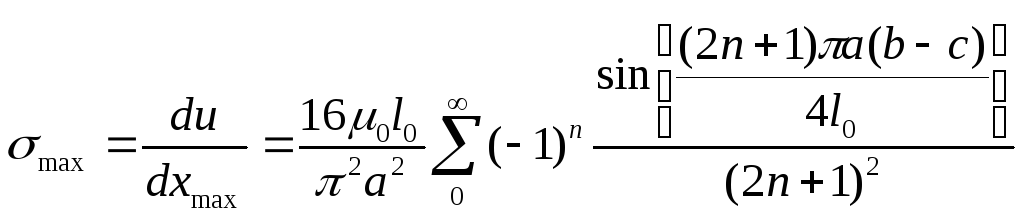(14)

Трапециидальный импульс.

Соотношение запишется

По теореме обращения перехода к оригиналу

(17)

Обозначим

(18)

(19)

Однозначна относительно Р имеет полюс третьего порядка в точке Р=0 и , где ω – определяется выражением (10).В точке Р=0 по формуле (10)’ имеем

(20)

Подставляя в (20) (19), то есть дифференцируем дважды с учетом (18) и получим в точкевычет находим по формулам (11)”

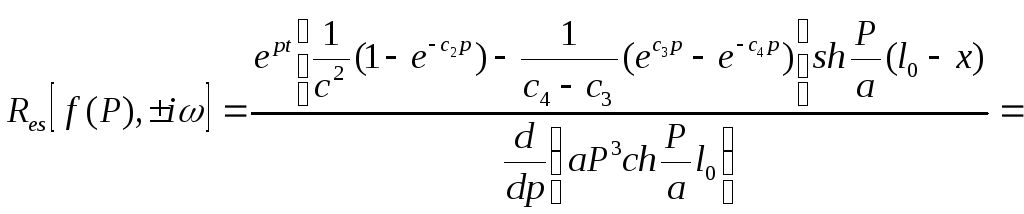
(21)

Преобразуем (21) и запишем для каждого знака отдельно:

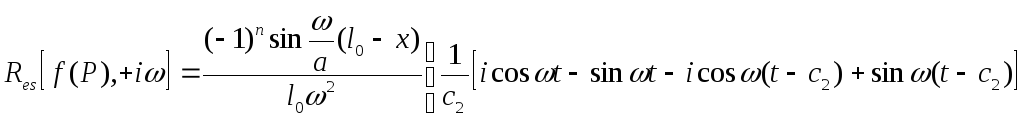
С учетом последних соотношений формула (21) примет вид:

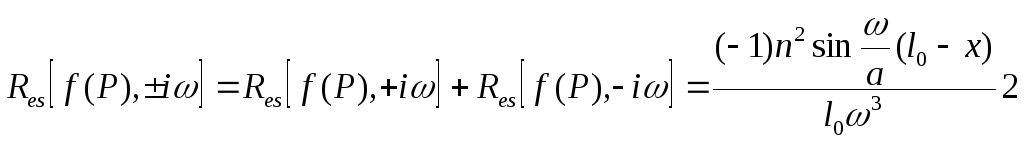
(22)

После преобразования тригонометрических функций, стоящих в фигурных скобках соотношение (22) получается

(23)

Соотношение (16) с учетом (23) запишется:

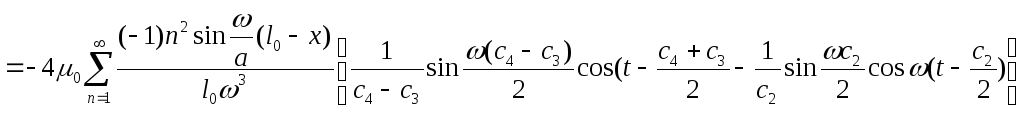
Выражение для деформации в виде бесконечного ряда. Исследование максимум значения будет, когда

, то есть

Максимально при x=0. максимальное значение принимает в моментt? моментn=0, то есть первый ряд (24) имеет максимальное значениеn=0x=0 подставим (24) получаем:

(25)

Максимум (25) когда первое произведение равно 0.

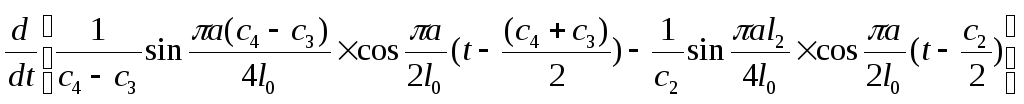
Обозначим , , тогда

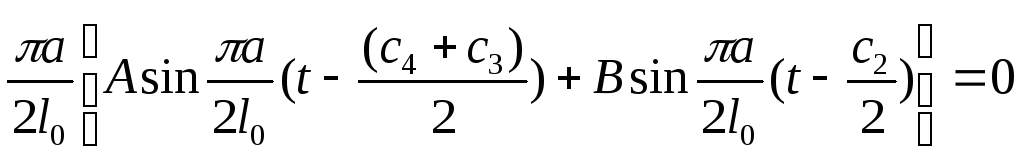(26)

(27)

При этом должно выполняться условие , при значенииtудовлетворяющие условию (27) имеет экстремальное значение . пустьt=t₁решение уравнения (27) и соответственно максимальные деформации (25), тогда соотношение с формулой (14) при учете (25) запишем выражения:

Или для любого значения

(30)

Ряд (30) аналогично ряду (24) является знакопостоянным абсолютно сходящимся.

Синусоидальный.

, где 0<t<c₁

Импульс такого вида можно получить сложением двух синусов одна из которых смещена относительно другой на время с₁.

и

Изображение

Переходим к оригиналу:

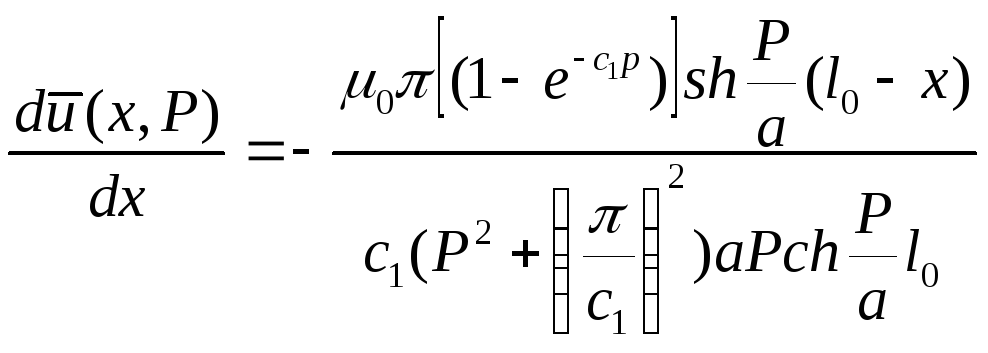(8)”’

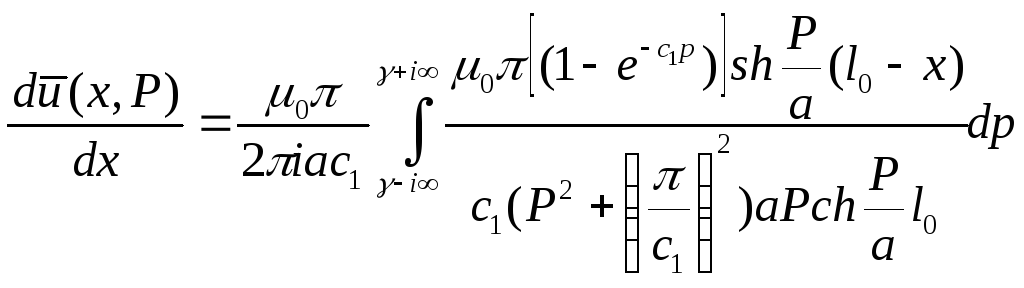(35)

Однозначно имеет кривые полюса в точках ,,.

Вычислим вычеты относительно этих полюсов.

В точках по формуле (10)”

В точках вычет находим по формуле

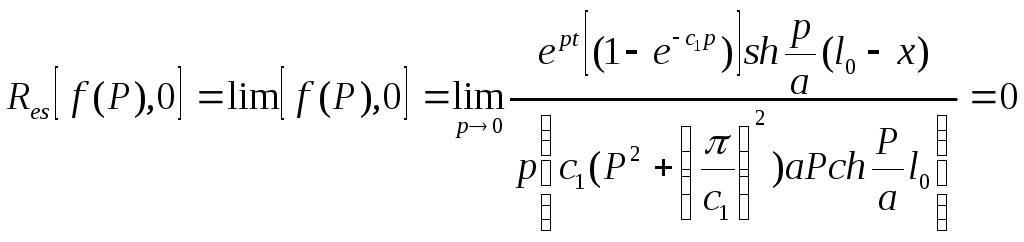
В точках вычеты определяются по формуле (10)”

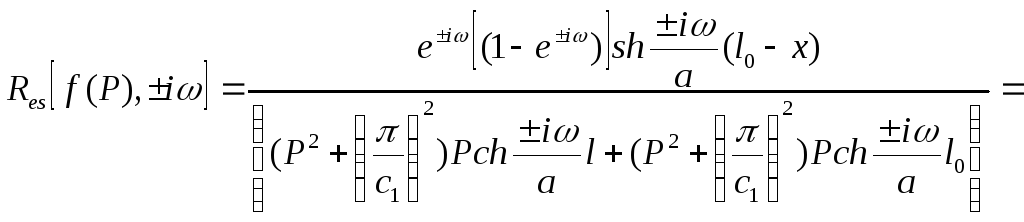
(36)

Запишем вычеты отдельно для каждого знака:

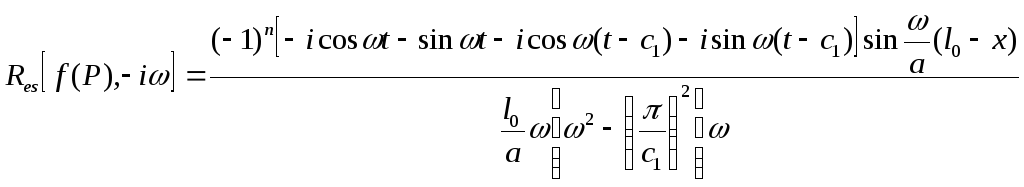
С учетом последних соотношений формула (36) запишется

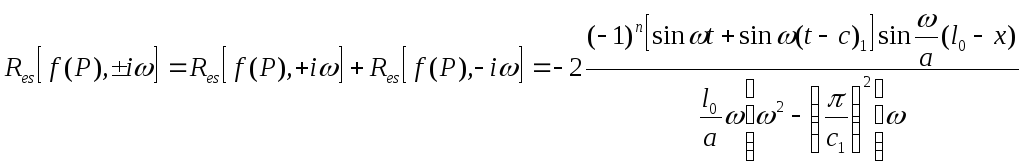
После преобразования

(38)

Соотношение (35) с учетом (38) запишется в виде

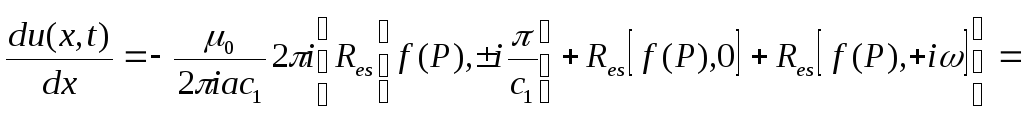
(39)

Выражение (39) представляет собой бесконечный знакопеременный абсолютны сходящийся ряд. Максимальные деформация будет, когда

,(40)

Из (40) с учетом (10) следует максимальная деформация реализуется в сечении k=0 в момент времени. Таким образом, выражение для максимальной деформации имеет вид

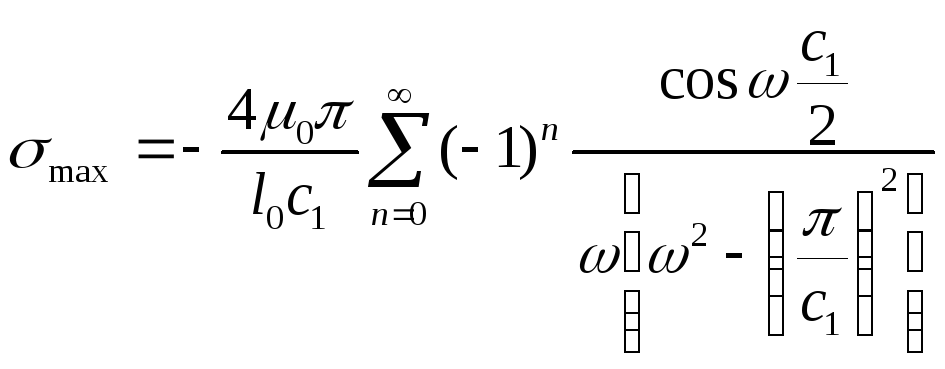(41)

Максимальное напряжение:

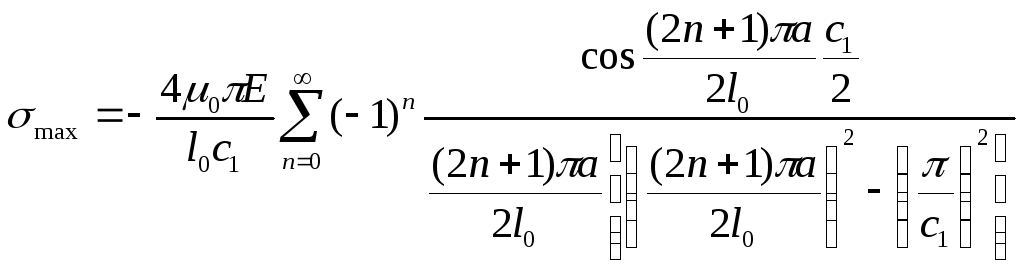(42)