Знаходження невідомого множника, діленого та дільника

Перед ознайомленням з правилом знаходження невідомого множника необхідно повторити взаємозв’язок арифметичних дій додавання та віднімання, множення та ділення, а також пригадати, що невідомий доданок знаходимо оберненою дією – відніманням, аналогічно – невідомий множник – дією ділення. Щоб одержати перший доданок, треба від суми відняти другий доданок; відповідно, щоб одержати перший множник, треба добуток поділити на другий множник. Так само робимо висновок щодо знаходження другого множника. Узагальнюємо ці правила:

Щоб знайти невідомий , требавідомий.

Правила знаходження невідомого діленого або дільника виводяться на підставі аналогії з правилами знаходження невідомого зменшуваного або від’ємника. Учні порівнюють арифметичні дії віднімання та ділення, визначають у них спільне (ділення можна замінити відніманням однакових чисел, доки не одержимо нуль; і при відніманні, і при діленні в результаті одержуємо менше число; і при відніманні, і при діленні компоненти називаються по-різному – за характером дій, що відбуваються з числами: зменшуване – ділене, від’ємник – дільник, причому зменшуване чи ділене має бути не менше, а більше від’ємника чи дільника або дорівнювати їм відповідно).

Отже, зменшуване та ділене – „велике” число. Учні згадують, що велике число на першому ступені знаходять додаванням (тому зменшуване знаходять додаванням), а на другому ступені – множенням (тому ділене знаходять множенням). Формулюємо правило знаходження невідомого зменшуваного та за аналогією відтворюємо правило знаходження невідомого діленого:

Щоб знайти невідоме , треба.

З’ясовуємо, що від’ємник має бути менший від зменшуваному або дорівнювати йому, так само дільник – менший за ділене або дорівнює йому. Менше число на першому ступені знаходять дією віднімання, тому від’ємник знаходять відніманням; а на другому ступені менше число знаходять дією ділення, тому дільник знаходять діленням. За аналогією з правилом знаходження невідомого від’ємника учні формулюють правило знаходження невідомого дільника:

Щоб знайти невідомий 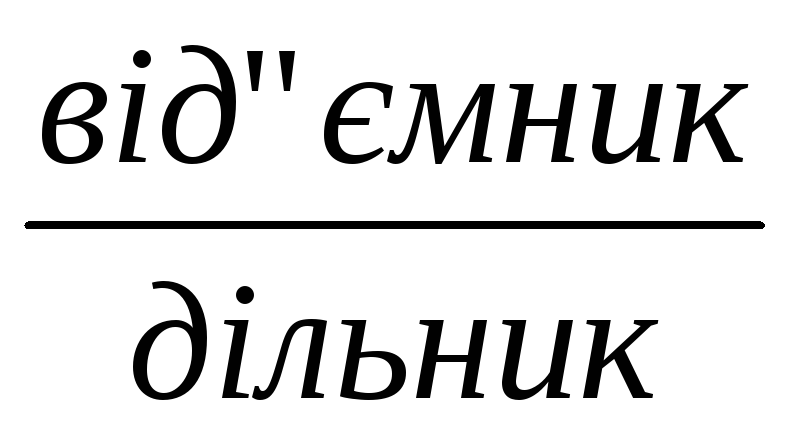, треба.

Ці правила школярі мають формулювати та застосовувати при виконанні вправ на знаходження невідомого компонента арифметичних дій.

Збільшення або зменшення числа в кілька разів. Кратне порівняння.

Відношення кратного порівняння вводиться на основі паралельного порівняння різницевого та кратного відношень. Розглянемо зміст підготовчих завдань.

Пропонуємо учням покласти в рядок 3 квадрати, а нижче покласти стільки квадратів, щоб їх було на 2 більше, ніж у верхньому рядку. Діти визначають, що в нижньому рядку квадратів на 2 більше – „стільки, скільки й у верхньому та ще 2”; стільки ж та ще 2 знаходять дією додавання; у верхньому рядку на 2 квадрати менше – „стільки ж, але без 2”; стільки ж, але без 2 знаходять дією віднімання.

Після відповідної роботи учні викладають у верхньому рядку 3 квадрати, а нижче під ними – два рази по три квадрати. З’ясовуємо, що в нижньому рядку квадратів більше, тому що поклали два рази по стільки, скільки й у першому рядку. Учитель повідомляє, що в цьому випадку кажуть, що в нижньому рядку в 2 рази більше квадратів, ніж у першому. Визначаємо, де квадратів менше. У верхньому рядку лише один раз по 3 квадрати, а в нижньому – два рази по 3 квадрати, тому у верхньому рядку в 2 рази менше квадратів, ніж у нижньому. Діти дістають висновку:

Для того, щоб стало в 2 рази більше, ніж 3, треба по 3 взяти 2 рази.

Для того, щоб стало в 2 рази менше, ніж 6, треба 6 розділити на дві рівні частини.

З метою засвоєння понять „збільшення або зменшення числа в кілька разів”, учні виконують практичні вправи типу:

Покладіть ліворуч 2 квадрати, а праворуч в 4 рази більше. Що треба зробити, що покласти в 4 рази більше квадратів? ( По 2 квадрати взяти 4 рази) Якою дією можна обчислити, скільки квадратів треба покласти? (Дією множення). Скільки буде, якщо по 2 взяти 4 рази? Діти обчислюють і перевіряють перерахунком.

Покладіть до верхнього рядка 15 трикутників, а до нижнього – в 3 рази менше. Що слід зробити, щоб покласти в 3 рази менше, ніж 15 трикутників? (Треба 15 розділити порівну на 3.) Якою арифметичною дією можна обчислити, скільки трикутників треба покласти до нижнього рядка? (Дією ділення.) Обчислюємо та перевіряємо перерахунком.

Р

Більше число знаходять або дією додавання, або дією множення. Додаванням знаходимо число, яке на кілька одиниць більше за дане, а множенням знаходимо число, яке в кілька разів більше даного числа.

Менше число знаходимо або відніманням, або діленням.

езультати співставлення збільшення або зменшення на кілька одиниць та в кілька разів можна подати у вигляді опорного конспекту.

на “ + “ БІЛЬШЕ

в “ ^. “

на “ – “ МЕНШЕ

в “ : “

в “ : “

Віднімаємо тоді, коли шукане число на кілька одиниць менше даного, а ділимо тоді, коли шукане число в кілька разів менше певного числа.

Правило кратного порівняння також вводиться на підставі паралельного порівняння з різницевим порівнянням. Актуалізуємо правило різницевого порівняння (щоб дізнатися, на скільки одне число більше чи менше за інше число, треба від більшого числа відняти менше), збільшення (зменшення) числа на кілька одиниць або в кілька разів.

Пропонуємо учням накреслити відрізок АВ довжиною 2 см. Під ним накреслити відрізок МК, довжина якого в 5 разів більша за довжину відрізка АВ. З’ясовуємо, який відрізок довший. У скільки разів відрізок МК довший за відрізок АВ? Щоб про це дізнатися, треба підрахувати скільки разів у довжині відрізка МК міститься по 2 см, що знайдемо арифметичною дією ділення. Отже, щоб дізнатися, в скільки разів одне число більше за інше, треба розділити більше число на менше.

Визначаємо, який відрізок має меншу довжину та в скільки разів. Довжина відрізка АВ у стільки разів менша за довжину відрізка МК, скільки разів довжина відрізка МК більша за довжину відрізка АВ. Таким чином, щоб дізнатися, в скільки разів одне число менше за інше, треба більше число поділити на менше.

Зіставляємо правила різницевого та кратного порівняння і формулюємо узагальнене правило:

Щоб дізнатися скількиодне число більше чи менше за інше, требабільшчислменше число.

На цьому етапі корисні вправи, у яких треба дізнатися, на скільки одне число більше чи менше іншого та в скільки разів воно більше чи менше даного числа, тобто для однієї й тієї самої пари чисел (в тому числі й величин).