Назви компонентів і результатів арифметичних дій множення та ділення

Познайомити з назвою компонентів і результату дій множення та ділення можна на підставі аналогії між діями множення та додавання, діями ділення та віднімання. Корисно підкреслити, що множення визначається через додавання, а ділення – через віднімання. Виходячи з цього, у дій додавання та множення, віднімання та ділення повинно бути багато спільного. По-перше, спільне можна побачити в назвах компонентів цих дій: при додаванні та множенні компоненти, з якими виконують дії, називаються за характером дії (додають – доданок, множать – множник), однаково, лише кажуть про порядок: перший , другий; а при відніманні та діленні – по-різному: більше число, яке зменшується в результаті віднімання та ділення, називають, а число , яке віднімають або на яке ділять,називають відповідно тієї дії, що виконують –.

У результаті додавання та множення отримаємо більше число, і воно називається відповідно „значення ”, а в результаті віднімання та ділення отримаємо менше число порівняно з вихідним, і воно називається„значення ”.

Числа, які множать, називаються множниками. Число, яке дістаємо при множенні, називають значенням добутку.

добуток

7 ^. 3 = 21

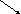
Перший

множник

Другий

множник

Значення

добутку

Виходячи з конкретного змісту арифметичної дії множення (множення можна замінити сумою однакових доданків), перший множник показує, яке число є однаковим доданком, а другий – скільки разів його слід додати!

Якщо два числа поєднані знаком множення, то записаний математичний вираз – добуток. Щоб записати добуток двох чисел, треба поєднати їх знаком множення.

Число, яке ділять, називається діленим. Число, на яке ділять – дільником. Число, яке дістаємо при діленні, називають значенням частки.

Частка

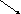14 : 2 = 7

значення

частки

значеннячастки

ділене

дільник

дільник

дільник

Якщо два числа поєднані знаком ділення, то записаний математичний вираз – частка. Щоб записати частку двох чисел, треба поєднати їх знаком ділення.

Переставний закон дії множення

Теоретичну основу побудови таблиць множення складає переставний закон дії множення. Використання цього закону полегшує складання таблиць і зменшує число табличних випадків для запам’ятовування. Тому доцільно познайомити учнів з переставним законом відразу після засвоєння конкретного змісту дії множення.

Переставний закон дії множення вводиться на підставі аналогії з переставним законом дії додавання:

• Як називаються числа при додаванні? (Доданок, доданок, значення суми). Цікаво, що компоненти дії додавання називаються однаково – доданки.

• У результаті додавання отримаємо більше чи менше число? (У результаті додавання отримаємо більше число, сума більша за доданки, якщо доданки відмінні від 0)

• Сформулюйте та запишіть переставний закон додавання. (Від перестановки доданків значення суми не змінюється. Числа можна додавати в будь-якому порядку: а + в = в + а)

• Яку арифметичну дію можна замінити множенням? (Множення – це додавання однакових доданків.)

• Як називаються числа при множенні? ( Множник, множник і значення добутку.)

• Цікаво, що компоненти при множенні називаються однаково. Це в них є спільним!

• У результаті множення отримаємо більше чи менше число? (Більше, значення добутку більше за кожний множник, якщо множники відмінні від нуля або одиниці.)

• Згадайте, чи не зустрічали ми раніше таку арифметичну дію, в якій компоненти називалися однаково, а в результаті отримували більше число? (Так, це дія додавання).

• Що ми знаємо про дію додавання? (Дії додавання притаманний переставний закон.)

• Дізнаємося, чи властивий переставний закон дії множення.

• Що треба змінити в записі переставного закону додавання, щоб отримати переставний закон множення? ( Треба змінити знак “+” на знак “ ^. ”. Отримаємо : а ∙ в = в ^∙ а. )

• Це треба перевірити. Наведіть приклади на застосування переставного закону множення. ( 5 ^. 3 повинно дорівнювати 3 ^. 5. Перевіримо це: 5 ^. 3 = 5 + 5 + 5 = 15, 3 ^. 5 = 3 + +3 + 3 + 3 + 3 = 15, 15=15 – це правильна рівність.)

• Який висновок можна зробити? (Дії множення притаманний переставний закон.) Сформулюйте переставний закон множення. Що треба змінити в формулюванні переставного закону додавання? Від перестановки множників значення добутку не змінюється. Числа можна множити в будь-якому порядку.

Можна поєднати формулювання переставного закону додавання та множення:

Переставний закон

Від перестановки значенняне змінюється.