Тема 3. Методика навчання додавання та віднімання двоцифрових чисел
Тема "Додавання та віднімання двоцифрових чисел у межах 100" опрацьовується через ознайомлення учнів з питаннями: усне додавання і віднімання двоцифрових чисел без переходу через десяток; усне додавання та віднімання двоцифрових чисел з переходом через десяток; письмове додавання та віднімання двоцифрових чисел.
Виокремлення усних і письмових обчислень пояснюється тим, що вони ґрунтуються на різних теоретичних основах. Письмові обчислення відрізняються від усних алгоритмами. Усні обчислення починаються з одиниць вищого розряду і записуються в рядок, а письмові обчислення починаються з нижчого розряду і записуються у стовпчик. Додавання та віднімання у стовпчик проводиться над кожним розрядом окремо і зводиться до додавання і віднімання в межах 20. Свідоме засвоєння письмових прийомів додавання та віднімання двоцифрових чисел є запорукою успішного використання їх для будь-яких чисел.
Під час вивчення додавання та віднімання двоцифрових чисел головним є зосередження уваги на способах виконання цих дій.
Аналіз способів додавання та віднімання чисел в межах 100 свідчить, що для їх свідомого виконання учні мають добре знати нумерацію чисел у межах 100, таблиці додавання одноцифрових чисел і відповідні випадки віднімання та засвоїти правила, які є наслідком з основних властивостей дій додавання і віднімання: додавання числа до суми, віднімання числа від суми, додавання суми до числа і віднімання від числа суми, додавання суми до суми, віднімання суми від суми, віднімання різниці від числа.
У таблиці показано, як групуються способи обчислення відповідно до названих правил.
|
Властивість |
Способи обчислення та їх обґрунтування |
|
Додавання числа до суми |
1) 56+30=(50+6)+30=(50+30)+6=80+6=86 2) 86+3=(80+6)+3=80+(6+3)=80+9=89 3) 46+4=(40+6)+4=40+(6+4)=40+10=50 4) 27+5=(20+7)+5=20+(7+5)=20+12=32 5) 22+16=(20+2)+16=(20+16)+2=36+2=38 6) 37+24=(30 +7)+24=(30+24)+7=54+7=61 7) 37+24=(31+6)+24=31+(6+24)=31+30=61 Замінили перший доданок сумою розрядних або зручних доданків і додали до цієї суми другий доданок найзручнішим способом. |
|
Віднімання числа від суми |
1) 56-30=(50+6)-30=(50-30)+6=20+6=26 2) 67-4=(60+7)- 4 = 60 + (7 - 4) = 60 + 3 = 63 3) 40 - 2=(30+10) - 2=30+(10 - 2)=30 + 8 = 38 4) 56 - 9=(40+16) - 9=40+(16 - 9)=40+7 = 47 5) 47 - 19=(8+39) - 19=8+(39 - 19)=8+20 = 28 Замінили зменшуване сумою розрядних або зручних доданків і відняли від цієї суми від'ємник найзручнішим способом. |
|
Додавання суми до числа |
Замінили другий доданок сумою розрядних або зручних доданків і додали суму до першого доданка зручним способом |
|
Віднімання суми від числа |
1) 70 - 26=70 - (20+6)=(70- 20) - 6=50– 6 = 44 2) 46 - 26=46 - (20+6)=(46–20) - 6=26 – 6= 20 3) 47 - 19=47 - (10+9)=(47 - 10) - 9=37 - 9= 28 4) 56 - 9 = 56 - (6 + 3) = (56 – 6) - 3 = 47 5) 47 – 19=47 – (17+2)=(47–17)– 2=30 – 2=28 Замінили від'ємник сумою розрядних або зручних доданків, а потім знайшли різницю найлегшим способом |
|
Додавання суми до суми |
1) 34+12=(30+4)+(10+2)=(30+10)+(4+2)=40 + +6 = 46 2) 35 + 25 = (30 + 5) + (20 + 5) = (30 + 20) + +(5 + 5) = 50 + 10 = 60 3) 34 + 18 = (30 + 4) + (10 + 8) = (30 + 10) + +(4 + 8) = 40 + 12 = 52 Замінили обидва доданки сумою розрядних доданків і виконали порозрядне додавання |
|
Віднімання суми від суми |
1) 34 - 12=(30+4) - (10+2)= (30 - 10) +(4 - 2) = =20 + 2 = 22 2) 70 - 26=(60+10)- (20+6)=(60 - 20)+(10- 6) = =40 + 4 = 44 Зменшуване розкладається на суму розрядних або зручних доданків, а від'ємник - на розрядні доданки |
|
Додавання різниці до числа |
Другий доданок замінили зручною різницею |
|
Віднімання різниці від числа |
1) 47 – 9=47 – (10 – 1)=(47 – 10)+1=37+1= 38 2) 47 - 19=47 - (20 - 1)=(47 - 20)+1=27+1=28 Від'ємник замінили зручною різницею |
Треба зазначити, що останні два випадки, наведені в таблиці, мають ще й іншу теоретичну основу – знання зміни суми в залежності від зміни одного з доданків та зміни різниці в залежності від зміни від’ємника. На цих теоретичних засадах здійснюється спосіб округлення.
Крім того, визначені правила здебільшого вводяться на пропедевтичному рівні: їх засвоєння всіма учнями не є обов’язковим.
Із аналізу способів обчислення видно, що всі вони зводяться до заміни одного або двох компонентів дій сумою таких двох доданків, над якими зручно виконувати обчислювальні дії. Такими доданками найчастіше є розрядні доданки. Але, як бачимо, в деяких розв’язаннях більш доцільним є розкладання числа на так звані "зручні" доданки.
З таблиці видно, що значення одного й того самого виразу можна обчислити різними способами. Пропонуючи учням виконати розв’язання різними способами, розвиваємо в них варіативність мислення, формуємо такі властивості обчислювальних навичок, як усвідомленість, раціональність тощо. Крім того, одержання однакового результату в обчисленнях різними способами непрямо свідчить про правильність відповіді.
Отже, ми розкрили загальні теоретичні положення до вивчення теми "Додавання і віднімання двоцифрових чисел у межах 100".
Відносно методичних підходів, то їх основні відмінності, передусім полягають у послідовності опрацювання основних питань теми. Наприклад, за методичною системою Л.П. Кочиної розглядається така послідовність: усне додавання і віднімання двоцифрових чисел без переходу через десяток; усне додавання та віднімання двоцифрових чисел з переходом через десяток; письмове додавання та віднімання двоцифрових чисел. На відміну від Л.П. Кочиної, М.В. Богданович пропонує письмовий прийом після вивчення усного додавання та віднімання без переходу через десяток; а усне обчислення з переходом через десяток дає після вивчення письмового прийому.
Власну послідовність розгляду усних та письмових прийомів Л.П. Кочина пояснює тим, що в більшості дітей на даний період уже добре сформовані обчислювальні навички, тому немає потреби відводити багато часу на розгляд письмових обчислень. За такого підходу створюються умови систематичного порівняння обох способів обчислення і формування в учнів уміння орієнтуватися в конкретній ситуації: "вибираю той спосіб обчислення, який для мене зручніший". З цією метою учням пропонуються завдання такого характеру: "За власним вибором розв'яжіть приклади в стовпчик. Решту прикладів розв'яжіть усно, записуючи лише відповіді".
Ще один доказ на користь цього підходу полягає в тому, що якщо не навчити дітей прийомам усного додавання та віднімання з переходом через розряд (які, до речі, є досить важкими), а познайомити їх відразу з письмовим прийомом, то створяться умови, коли діти, навіть звертаючись до хитрощів, не будуть лічити усно, а лише у стовпчик!
Тим часом, М.В. Богданович обґрунтовує введення письмового прийому перед вивченням усного додавання і віднімання з переходом через розряд тим, що спочатку треба познайомити учнів з письмовими обчисленнями як найбільш легкими, а потім з усними – як найбільш складними. У подальшому письмові обчислення використовуються для перевірки усних.
Слід зазначити, що це не є істотним аргументом для вивчення додавання і віднімання в такій послідовності, оскільки дії додавання та віднімання є взаємо оберненими і існує прямий спосіб їх перевірки: правильність додавання перевіряється відніманням, а правильність віднімання можна перевірити додаванням; якщо при цьому одержуємо інший результат, ніж очікувано, то робимо висновок про те, що значення виразу знайдено неправильно.
Порівняння різних підходів до опрацювання теми „Додавання і віднімання двоцифрових чисел у межах 100" дозволяють виокремити основні їх відмінності.
Перша відмінність методичних підходів Л.П. Кочиної та М.В. Богдановича, передбачає різний порядок опрацювання усних та письмових прийомів додавання двоцифрових чисел. Друга відмінність полягає в тому, що за системою Л.П. Кочиної, методика вивчення додавання і віднімання двоцифрових чисел розглядається на основі одночасного опрацювання взаємно обернених дій (додавання і віднімання), а за системою М.В. Богдановича – на основі послідовного вивчення, тобто спочатку вивчається додавання, а потім віднімання. Третя відмінність пов’язується з послідовністю вивчення загальних і часткових випадків додавання і віднімання двоцифрових чисел. Перший методичний підхід Л.П. Кочиної полягає у вивченні спочатку часткових випадків додавання і віднімання двоцифрових чисел, а потім пропонується загальний випадок; за другим, який розкриває М.В. Богданович – учні відразу знайомляться з загальним випадком додавання та віднімання двоцифрових чисел (кожне з них містить і десятки, і одиниці) способом порозрядного обчислення, а потім з частковими випадками. Для віднімання з переходом через десяток автори двох методичних систем дотримуються одного й того ж погляду.
За методичним підходом Л.П. Кочиної додавання і віднімання двоцифрових чисел вивчається в такому порядку: 1) випадки додавання та віднімання виду: 45 + 2, 45 + 20, 45 – 2, 45 – 20; 2) випадки додавання виду: 56 + 4; 3) додавання та віднімання виду 34 + 52 і 76 – 44 (по частинах); 4) додавання та віднімання виду 34 + 52 і 76 – 44 (порозрядно).
На думку М.В. Богдановича спочатку доцільно розглядати загальні випадки додавання і віднімання двоцифрових чисел, а потім часткові.
Розглянемо більш докладно опрацювання теми "Додавання та віднімання двоцифрових чисел у межах 100", оскільки такий методичний підхід відповідає вимогам Державного стандарту початкової загальної освіти та нової навчальної програми для учнів початкової школи.
Усне додавання та віднімання без переходу через десяток
Додавання (віднімання) одноцифрового числа до (від) двоцифрового без переходу через розряд. Ознайомлення з такими випадками здійснюється на підставі практичних вправ із намистинками або розгляду малюнків, за якими складають рівності.
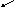
Коментар до першого малюнка: було 6 одиниць, приєднали – додали ще 3 одиниці, стало 9 одиниць: 6 + 3 = 9.
Коментар до другого малюнка: було 16 – це 1 десяток і 6 одиниць; до 16 додали 3; 3 одиниці приєднали – додали до 6 одиниць, одержали 9 одиниць; отже, маємо 1 десяток і 9 одиниць – це число 19: 16 + 3 = 19... У результаті аналогічних вправ учні дістають висновку: одиниці додають до одиниць!
Виконуємо розгорнений запис:
|
|
1 |
5 |
+ |
4 |
= |
1 |
0 |
+ |
5 |
+ |
4 |
= |
1 |
0 |
+ |
9 |
= |
1 |
9 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
0 |
+ |
5 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Перший доданок – число 15 – подаємо у вигляді суми розрядних доданків: 15 = 10 + 5; до суми 10 і 5 треба додати 4; додаємо 4 одиниці до 5одиниць: 5 + 4 = 9; до 10 додаємо одержане число 9: 10 + 9 = 19...
Аналогічно розглядається віднімання. За допомогою практичних дій з намистинами або розгляду малюнків діти переконуються, що одиниці віднімають з одиниць.
|
|
1 |
7 |
- |
4 |
= |
1 |
0 |
+ |
7 |
- |
4 |
= |
1 |
0 |
+ |
3 |
= |
1 |
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
0 |
+ |
7 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Зменшуване 17 подаємо у вигляді суми розрядних доданків 10 і 7; будемо від суми 10 і 7 віднімати число 4; 4 одиниці віднімаємо з 7 одиниць, буде 3; до числа 10 додаємо результат віднімання одиниць – число 3, одержимо 13.
У результаті аналізу власної діяльності школярі формулюють ООД (орієнтувальну основу дії):
одноцифрового
числа
двоцифрового без переходу через розряд
Двоцифрове число замінюю сумою десятків та одиниць;
одиниці
одиниць.До десятків додаю одержаний результат.
Додавання (віднімання) круглого числа до (від) двоцифрового. Ознайомлення з новим способом дії здійснюється аналогічно. Проілюструємо його на прикладі віднімання.
– Яке число
позначено намистинками? (84) Скільки в
ньому десятків? (8 десятків.) Скільки
одиниць? (4 одиниці.) Віднімемо 5 десятків
або 50. З 8 десятків віднімемо 5 десятків.
Одержимо 3 десятки та ще 4 одиниці.
Складаємо рівність: 84 – 50 = 34. Дістаємо
висновку: десятки віднімають з десятків!
Виконуємо розгорнений запис:
|
|
5 |
7 |
- |
4 |
0 |
= |
5 |
0 |
+ |
7 |
- |
4 |
0 |
= |
1 |
0 |
+ |
7 |
= |
1 |
7 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
5 |
0 |
+ |
7 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Двоцифрове зменшуване 57подаємо у вигляді розрядних доданків 50 і 7; з цієї суми будемо віднімати число 40; десятки віднімаємо з десятків: 50 – 40 = 10; до одержаного результату 10 додаємо 7 одиниць, буде 17.
У результаті аналізу власної діяльності школярі формулюють ООД:
круглого
числа
двоцифрового
Двоцифрове число замінюю сумою десятків та одиниць.
десятки
десятків.До одержаного результату додаю одиниці.
О
Перший доданок
число – 51, це 5 десятків та 1 одиниця;
другий доданок – число 17, це 1 десяток
і 7 одиниць. Десятки додаємо до десятків
(5 д. + 1 д. = 6 д.); одиниці додаємо до одиниць
(1 + 7 = 8).
1 5 1 7 6 8
+ = =
Одержали число, що містить 6 десятків і 8 одиниць – це число 68.
Таким чином, діти дістають висновку: при додаванні двоцифрових чисел десятки додають до десятків, а одиниці додають до одиниць. Отже, виконуємо дії окремо з десятками і окремо з одиницями – порозрядно, тому цей спосіб називається способом порозрядного додавання.
Ознайомлюємо учнів із способом порозрядного віднімання двоцифрових чисел без переходу через розряд, ставлячи проблемне запитання: Чи можна так само міркувати при відніманні двоцифрових чисел?
Зменшуване –
число 75, це 7 десятків та 5 одиниць,
від’ємник – 43, це 4 десятки та 3 одиниці.
Десятки віднімаємо з десятків (7 д. – 4
д. = 3 д.), а одиниці віднімаємо з одиниць
(5 – 3 = 2); одержали число, яке містить 3
десятки і 2 одиниці – це число 32.
7 5 4 3 3 2
- =
Таким чином, дістаємо висновку: при відніманні двоцифрових чисел десятки віднімають з десятків, а одиниці віднімають з одиниць. Отже, виконуємо дії окремо з десятками і окремо з одиницями – порозрядно, тому цей спосіб називається способом порозрядного віднімання.
У результаті аналізу власної діяльності школярі формулюють ООД:
Додавання та віднімання двоцифрових чисел
1. Замінюю кожне число сумою десятків і одиниць.
2. 
десятки.
3
.
одиниці.
4
. Додаю
одержані числа.
Наприклад:
45 + 34 = 40 + 5 + 30 + 4 = 70 + 9 = 70
40+5
30+4
68
– 36 = 60 + 8 – 30 – 6 = 30 + 2 = 32
60+8 30+6
Додавання та віднімання по частинах. Ознайомлення із способом додавання і віднімання по частинах для двоцифрових чисел здійснюється під час порівняння пар записів:
34+10+2=44+2=46 47–20–4=27-4=23 25+50+3=75+3=78
34+12 47–24 25+53
Обчислюємо значення першого виразу і встановлюємо, що воно може допомогти обчислити значення другого виразу. Аналізуючи виконувані дії, встановлюємо, як можна міркувати при додаванні і відніманні двоцифрових чисел, формулюємо ООД:
Додавання та віднімання двоцифрових чисел по частинах
1. Замінюю
сумою десятків і одиниць.
2. 
десятки.
3. 
одиниці.
Наприклад:
43 + 26 = 43 + 20 + 6 = 63 + 6 = 66
20+6
58
– 35 = 58 – 30 – 5 = 28 – 5 = 23
30+5
К
орисно
порівняти способи порозрядного додавання
та віднімання зі способами обчислення
по частинах.
53
+ 26 = 50 + 3 + 20 + 6 = ... 96 – 64 = 90 + 6 – 60 – 4 =
50+3 20+6 90+6 60 + 4
5
3
+ 26 = 53 + 20 + 6 = ... 96 – 64 = 96 – 60 – 4 =
...
20+6 60+4
При порозрядному обчисленні ми кожне число замінюємо сумою розрядних доданків, а при обчисленні по частинах замінюємо лише другий доданок або від’ємник сумою розрядних доданків.
На наступному етапі вводяться випадки додавання, коли сума одиниць дає число 10, та випадки віднімання з круглих десятків одноцифрового числа.
О
Учні
встановлюють, що змінився другий
доданок; це вплинуло на те, що при
додаванні одиниць до одиниць одержали
число 10. Тому
наступним
76
+ 3 = 70 + 6 + 3 = 70 + 9 = 79 70+6
76
+ 4 = 70 + 6 + 4 = 70 + 10 = 80 70+6
кроком треба додавати круглі числа, а не записувати суму десятків та одиниць одним числом.
Теоретичною підставою розв’язання в обох випадках є правило додавання числа до суми. Тому це один і той же спосіб міркування.
Аналогічно вводимо новий випадок віднімання.
Учні
встановлюють, що змінилося зменшуване.
Це вплине на те, що його слід записати
не сумою десятків та одиниць, а сумою
зручних доданків, яка містить число
12
– 8 = 10 + 2 – 8 = 2 + 2 = 4
10+2
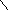40
– 8 = 30 + 10 – 8 = 30 + 2 = 32
30+10
10, тому що з 10 відніматимемо від’ємник 8. 8 віднімаємо з 10 і одержаний результат додаємо до іншого доданка.