1.7.2 Показатели вариации

Показатели вариации делятся на две группы: абсолютные и относительные. К абсолютным показателям вариации относятся:

• размах вариации;

• среднее линейное отклонение;

• дисперсия;

• среднее квадратическое отклонение.

Относительными показателями вариации являются:

• относительное линейное отклонение;

• коэффициент вариации и др.

Для иллюстрации расчетов этих показателей воспользуемся следующими данными:

Таблица 1.7.1

Распределение организаций по размерам среднемесячных затрат на рабочую силу

Группы организаций по средним размерам затрат на рабочую силу в % от среднеотраслевых затрат	Удельный вес предприятий по обследованным отраслям экономики, в % к итогу
до 30	13,2
30 – 50	28,6
50 – 75	24,9
75 – 100	13,6
100 – 150	12,2
150 – 250	5,7
250 – 300	1,8
Итого:	100

Самым простым показателем, уже использованным выше при группировке данных, является размах вариации. Он представляет собой разность максимального и минимального значений признака:

R = =300 – 0 = 300% (1.7.1)

Недостатком данного показателя является то, что он оценивает только границы варьирования признака и не отражает его колеблемость внутри этих границ. Для анализа вариации необходим и показатель, который отражает все колебания варьирующего признака, дающий обобщенную ее характеристику. В качестве такой величины можно условно принять среднюю величину из всех значений признака, так как в ней более или менее погашаются случайные отклонения от закономерного хода развития явления, и средняя тем самым отражает типичный размер признака у данной однородной совокупности единиц.

Такая средняя называется средним линейным отклонением (). Оно вычисляется как средняя арифметическая из абсолютных значений отклонений вариант хи (взвешенная или простая в зависимости от исходных условий) по следующим формулам:

(1.7.2) – простая формула;

(1.7.3) – взвешенная формула;

По данным нашего примера определим среднее линейное отклонение, построив для удобства расчетов вспомогательную табл. 1.7.2.

1) находим середины интервалов () по исходным данным (гр. 1) и записываем их в таблицу (гр. 3);

2) определим произведения значений середин интервалов () на соответствующие им веса (f) (гр. 4). В итоге получаем 7248,3. Рассчитаем среднюю величину по формуле средней арифметической взвешенной:

Таблица 1.7.2

Распределение организаций по размерам среднемесячных затрат на рабочую силу

Группы организаций по средним размерам затрат на рабочую силу в % от средне-отраслевых затрат х	Удельный вес предприя-тий по обследо-ванным отраслям экономики, в % к итогу f	Сере- дина ин- тер- вала ()
1	2	3	4	5	6	7
до 30	13,2	15,0	198,0	57,5	759	43642,5
30 – 50	28,6	40,0	1144,0	32,5	929,5	30208,75
50 – 75	24,9	62,5	1556,3	10	249	2490
75 – 100	13,6	87,5	1190,0	15	204	3060
100 – 150	12,2	125	1525,0	52,5	640,5	33626,25
150 – 250	5,7	200	1140,0	127,5	726,75	92660,63
250 – 300	1,8	275	495,0	202,5	364,5	73811,25
Итого:	100		7248,3		3873,25	279499,38

3) для расчета среднего линейного отклонения находим абсолютные отклонения середины интервалов, принятых нами в качестве вариантов признака () от средней величины () (гр. 5)

4) вычисляем произведения отклонений |-| на их веса (f)и подсчитываем сумму этих произведений (3873,25). Результаты заносим в гр. 6.

5) делим эту сумму на сумму весов, чтобы получить искомую величину :

Следующие абсолютные показатели, которые мы будем определять, это дисперсия и среднее квадратическое отклонение. Эти показатели являются общепринятыми мерами вариации и часто используются в статистических исследованиях.

Дисперсия представляет собой средний квадрат отклонений индивидуальных значений признака от их средней величины и вычисляется по формулам простой и взвешенной дисперсий (в зависимости от исходных данных):

(1.7.4) – простая формула;

(1.7.5) – взвешенная формула;

Среднее квадратическое отклонение определяется как квадратный корень из дисперсии и имеет ту же размеренность, что и изучаемый признак:

(1.7.6) – простая формула;

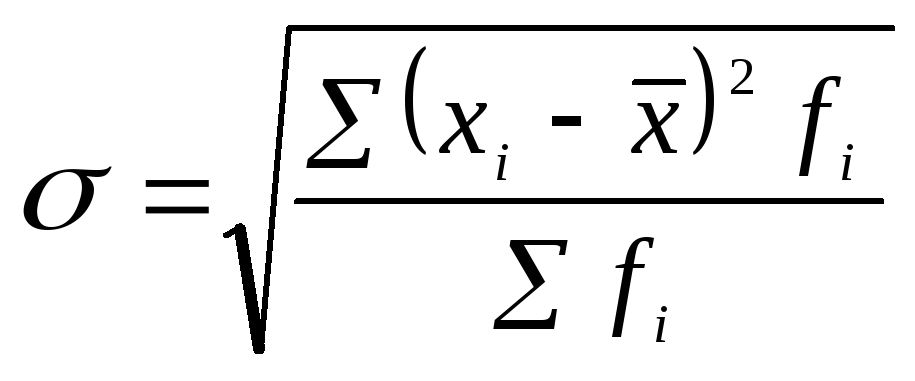(1.7.7) – взвешенная формула;

Рассмотрим расчет дисперсии и среднего квадратического отклонения по данным таблицы 1.7.2.

1) возводим отклонения отво вторую степень и умножаем на их веса f,затем подсчитываем сумму этих произведений. Эта сумма равна 279499,38. Результаты записываем в гр. 7.

2) разделив эту сумму на сумму весов, получаем дисперсию:

3) извлекая из дисперсии корень второй степени, получаем среднее квадратическое отклонение:

Степень вариации в данной совокупности велика, так как средняя величина равна 72,5%. Это говорит о том, что рассматриваемая нами совокупность неоднородна.

Рассмотренные показатели позволяют получить абсолютное значение вариации, т.е. оценивают ее в единицах измерения исследуемого признака. В отличие от них, относительное линейное отклонение и коэффициент вариации измеряет колеблемость в относительном выражении, относительно среднего уровня, что во многих случаях является предпочтительнее.

Относительное линейное отклонение ():

(1.7.8)

Определим значение этого показателя по нашим данным:

=38,7/ 72,5*100=53,4%

Коэффициент вариации ():

(1.7.9)

Определим значение коэффициента вариации по нашим данным:

=52,9/ 72,5*100=73,0%

Рассчитанная величина свидетельствует о значительном относительном уровне колеблемости признака. Если превышает 33%, то совокупность по рассматриваемому признаку можно считать неоднородной.

Следует отметить, что дисперсию используют не только для оценки вариации, но и при измерении взаимосвязей, для проверки статистических гипотез и т.п.

Дисперсия может быть рассчитана и по упрощенной формуле:

(1.7.10)

Как и любая средняя, дисперсия имеет определенные математические свойства:

а) если все значения признака х уменьшить (увеличить) на определенную величину, дисперсия не изменится;

б) если все значения признака изменить в k раз, то дисперсия изменится в k раз;

в) в случае замены частот частостями дисперсия не изменится.

Статистическое изучение вариации многих социально-экономических явлений проводится и при помощи дисперсии альтернативного признака, вариация которого имеет два взаимоисключающих значения – «1» (наличие данного признака) и «0» (отсутствие его), долю вариантов, обладающих данным признаком, р, и не обладающих им q. Так как ряд р + q = 1, то средняя , а дисперсия альтернативного признака , где , n – число наблюдений, m – число единиц совокупности, обладающее данным признаком, q = 1- р. Отсюда дисперсию доли альтернативного признака можно выразить следующим образом:

(1.7.11)

Пример. Экзамен по информатике сдали 25 человек из 30. Определим дисперсию доли студентов, не сдавших экзамен:

Наряду с изучением вариации признака по всей совокупности в целом часто бывает необходимо проследить количественные изменения признака по группам, на которые разделяется совокупность, а также и между группами. Такое изучение вариации достигается посредством вычисления и анализа различных видов дисперсии.