4.2.Напряжения на произвольной площадке при линейном напряжённом состоянии

Рассмотрим деталь произвольной формы ( рис. 4.2.1, а). Пусть хотя бы в одной точке этой детали реализуется линейное напряж¼нное

состояние. В окрестности этой точки вырежем бесконечно малый элемент и покажем его отдельно.

Рис. 4.2.1. Линейное напряж¼нное состояние

Пример такого нагружения брус при центральном растяжении или сжатии (рис. 4.2.1, б). Покажем, что при центральном растяжении действует лишь одно из главных напряжений. Вырежем в окрестности точки элемент, верхняя и нижняя грани которого перпендикулярны оси бруса. На этих гранях действует только нормальное напряжение,

Домашняя

JJ II

J I

Назад

На весь экран

Закрыть

касательных напряжений нет. На боковых гранях нет ни нормальных, ни касательных напряжений (слои друг на друга не давят), то есть имеет место линейное напряж¼нное состояние.

Рассмотрим произвольную площадку, проходящую через данную точку . Положение этой площадки (рис. 4.2.1, в) определяется нор-

малью , то есть углом ( ). Рассмотрим действие верхней части элемента на нижнюю. Вв¼дем следующее правило знаков для угла :

при повороте против хода часовой стрелки угол положительный, а при повороте по ходу часовой стрелки отрицательный. Если обозначить через площадь нижней грани элемента, то площадь наклонной пло-

щадки будет равна / .

Покажем нормальное и касательное напряжения, действую- щие на площадке , и выразим их через . Направим ось по направ-

лению , а ось и составим уравнения равновесия для нижней части элемента

Домашняя

JJ II

J I

Назад

На весь экран

Закрыть

Таким образом, мы получили формулы для определения напряжений на произвольной площадке при линейном напряж¼нном состоянии.

Проанализируем полученные формулы.

Формула для нормальных напряжений: =| | _наиб = при2 = 1 èëè ïðè = ±1; = ± , ãäå = 0, ±1, ±2, . . . , òî åñòü

при любых попадаем на те же главные площадки. Следовательно,

Следовательно, какое бы не брали, всегда будем попадать на одну из площадок, наклон¼нных к главным площадкам под углом 45 (ðèñ. 4.2.2). Строго говоря, | | наиб действуют по конической поверхности.

4.3.Напряжения на произвольной площадке при плоском напряжённом состоянии

Рассмотрим произвольно нагруженное тело (рис. 4.3.1,а). Выберем точку , в которой имеет место плоское напряж¼нное состояние, то есть элемент в этой точке нагружен лишь по двум граням. Вырежем в

Домашняя

JJ II

J I

Назад

На весь экран

Закрыть

Таким образом, мы получили формулы преобразования напряжений при повороте от главных площадок при плоском напряж¼нном состоянии.

Проанализуем полученные формулы

| |наиб= − ,

2

при sin 2 = ±1, откуда = ±4 + 2 .

Следовательно, наибольшие касательные напряжения равны полусумме главных напряжений и действуют на площадках, равнонаклон¼нных к главным (рис. 4.3.3).

Рис. 4.3.3. Положение площадок с наибольшими касательными напряжениями

Домашняя

JJ II

J I

Назад

На весь экран

Закрыть

4.4.Графический способ определения напря-

жений при плоском напряжённом состоянии. Круги Мора

В предыдущем параграфе были получены формулы для определения напряжений на произвольной площадке при плоском напряж¼нном состоянии

Если в этих формулах исключить , то получим зависимость =( ), которая в осях , отображает окружность с центром на оси . О.Х. Мор использовал это обстоятельство для определения напряжений графическим способом. При этом можно решить два вида задач.

I задача (прямая)

Äàíî: , , (ðèñ. 4.4.1). Требуется определить: , . Изложим последовательность операций, а затем докажем, что они

правомерны (рис. 4.4.2).

Провед¼м оси , и отложим отрезки, равные главным напряжениям = , = . На отрезке , как на диаметре, построим окружность с центром в точке . Полученная окружность называется

кругом Мора или кругом напряжений. Пров¼дем из центра окружности радиус под углом 2 от оси против хода часовой стрелки (так

Домашняя

JJ II

J I

Назад

На весь экран

Закрыть

Рис. 4.4.1. Определение напряжений на произвольной площадке

как считаем, что угол положительный) и докажем, что координаты полученной точки соответствуют напряжениям на площадке .

Итак, мы доказали, что с помощью круга Мора можно определить напряжения на произвольной площадке . Следовательно, задача ре-

øåíà.

Домашняя

JJ II

J I

Назад

На весь экран

Важный вывод: точки, соответствующие двум взаимно перпендикулярным площадкам, лежат на концах одного диаметра круга Мора.

II задача (обратная).

Дано: , , , . Требуется определить: , , 0( ).

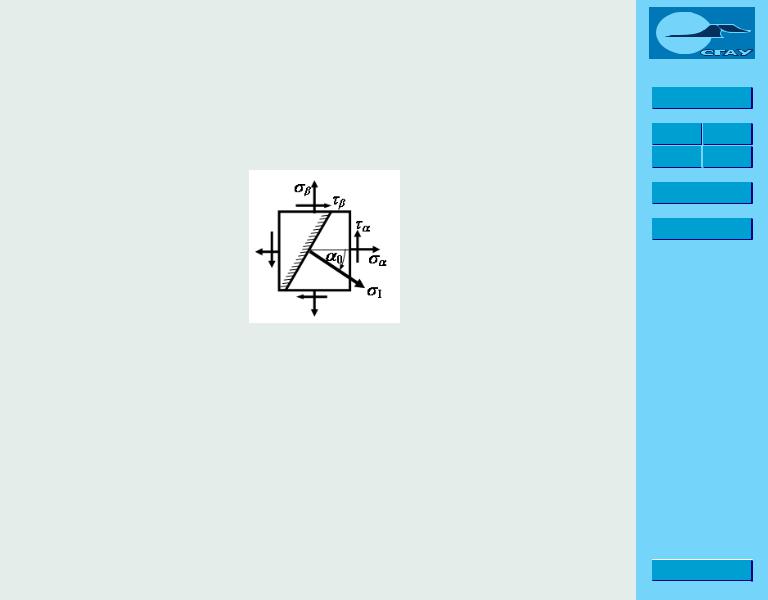
Рис. 4.4.3. Главные площадки и главные напряжения

Эта задача имеет для практики более важное значение, чем прямая задача.

Проводим координатные оси (рис. 4.4.4) , и строим в этих осях

точки ( , ) ( , ). Так как эти точки соответствуют взаимно перпендикулярным площадкам, то они лежат на концах одного диаметра круга Мора. Соединяем эти точки и определяем положение центра круга . Имея центр и диаметр, можно провести единственную

окружность. Задача решена.

Домашняя

JJ II

J I

Назад

На весь экран

Закрыть