взять реальное радиационное поле, сформированное в заданной точке внутри фантома. Понятно, что изменение размера, формы или состава фантома обусловливает изменение этого реального по­ля и, следовательно, изменение искомой дозиметрической величины, хотя исходное радиационное поле остается неизменным. В данном случае мы имеем дело с фантомно-зависимой эквивалентной дозой.

Типичная фантомно-зависимая величина — эффективная экви­валентная доза. К этому классу величин относится доза в крити­ческом органе, а также связанный с фантомом показатель (индекс) дозы, с которым подробнее мы познакомимся дальше.

Базисные дозиметрические величины по существу являются до­зиметрическими характеристиками исходного поля излучения. Лишь в отдельных частных случаях они могут служить адекват­ной мерой радиационного воздействия. Однако они удобны, срав­нительно легко определяются инструментальными методами.

Фантомно-зависимые дозиметрические величины расширяют возможности предсказания радиационно-индуцированного эффек­та. Проблема заключается в своеобразной оптимизации набора этих величин, обеспечивающей их максимальную адекватность при минимально возможном их числе.

Деление дозиметрических величин на базисные и фантомно-за­висимые в значительной степени условно. Правомерно, по-видимо­му, рассматривать базисные величины как частный случай фан­томно-зависимых: при непрерывном уменьшении объема фантома до нуля значение фантомно-зависимой дозиметрической величины приближается к значению соответствующей базисной величины. Тем не менее такое деление удобно как в теоретическом, так и в практическом плане. Связь этих двух классов величин между со­бой, а также связь каждой из них с базисным функционалом ис­ходного радиационного поля удобно выражать через переводные коэффициенты.

3. Переводные коэффициенты

Принимая флюенс Ф за исходную величину, любую другую до­зиметрическую величину М можно выразить следующим образом:

М=٠ (П2.2)

где &— коэффициент, переводящий значение флюенса Ф в значе­ние дозиметрической величины М; в этом смысле & — переводной коэффициент.

Соответственно двум классам дозиметрических величин — ба­зисным и фантомно-зависимым — можно сопоставить два класса переводных коэффициентов: базисные переводные коэффициенты и фантомно-зависимые переводные коэффициенты. Рассмотрим их несколько подробнее на отдельных примерах.

Базисные переводные коэффициенты связывают между собой базисные дозиметрические величины.

372

Керма-фактор 6 —коэффициент, переводящий значение флюен- са в значение кермы. При энергетическом равновесии керма-фак- тор переводит значение флюенса в значение поглощенной дозы.

Для моноэнергетических нейтронов с энергией Еп керма-фак- тор /г (£п) определяется следующей формулой:

3. .1 (ه)ا-،ة(_لر£)ر،ه]،ج = (ه4

где м_г —число ядер типа I в единице массы вещества, для кото- рого определяется керма. Индекс / характеризует вид ядерного взаимодействия нейтронов؛ а^(Еп) —поперечное сечение ؛-го вида взаимодействия с ядрами типа ٤'; £^(£?1)-средняя кинетическая энергия заряженных частиц, которые возникают при /-м виде вза- имодействия с ядрами типа ٠'٤

Заряженные частицы, о которых идет речь,— ядра отдачи при упругом и неупругом рассеянии, а-частицы, протоны и дейтоны от (и, а), (/г, р) и (п, ٥) реакций, а также электроны, возникающие в результате наведенной активност’И.

Среднее значение керма-фактора к для нейтронного излучения с энергетическим спектром ф(£п) можно рассчитать по формуле هي(ع)٢٠/عيل£)غل£)حهغ (П2.4)

где ф (£^) — флюенс нейтронов в энергетическом интервале от

Еп до Еп + ٥£п, а &(Е_п) определяется формулой (П2.3).

Многими исследователями выполнены расчеты керма-фактора в поле нейтронного излучения для материалов различного атомно- го состава. Особый интерес представляет керма-фактор для ткане٠ эквивалентного вещества. Результаты расчетов различных авто- ров несколько различаются даже для одного и того же энергети- ческого диапазона нейтронов. Это объяснимо, поскольку резуль- таты расчета чувствительны к небольшим изменениям элементного состава вещества, разбросу значений констант взаимодействия, учету или неучету различных ядерных реакций. Эта чувствитель- ность сама по себе неодинакова в разных энергетических диапа- зонах. Последнее обстоятельство заставляет для различных энер- гетических групп нейтронов составлять различные аналитические приближения, обеспечивающие приемлемую точность расчета.

На рис. 102 представлена энергетическая зависимость керма- фактора в тканеэквивалентном материале для моноэнергетических нейтронов в диапазоне от тепловых энергий до 60 МэВ. график представляет собой результат компиляции данных различных ав- торов.

В поле нейтронного излучения керма в тканеэквивалентном ма- териале формируется в основном короткопробежными тяжелыми заряженными частицами, что практически обеспечивает условия энергетического равновесия, в этих условиях керма-фактор слу-

373

Рис. 102. Энергетическая зависи­мость керма-фактора в тканеэкви­валентном материале для моно- энергетических нейтронов в диапа­зоне энергий от тепловых до 60 МэВ

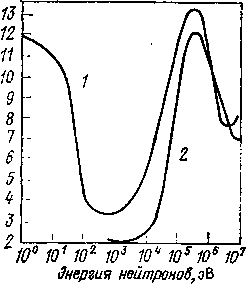
Рис. 103. Зависимость базисной величины — коэффициента качества к(Е_п) от энергии моноэнергетических нейтронов (/) и зависимость эффективного коэффи­циента качества к_Эф(٤о) для цилиндрического тканеэквивалентного фантома от энергии моноэнергетических нейтронов исходного поля (2)

жит также переводным коэффициентом от флюенса к поглощенной дозе.

Коэффициент качества излучения переводит значение поглощен­ной дозы в эквивалентную дозу. Коэффициенту качества припи­сывается определенное значение в зависимости от ЛПЭ частиц любого вида. Другими словами, принимают, что независимо от их вида частицы с одинаковым значением ЛПЭ имеют одинаковый коэффициент качества.

Моноэнергетические нейтроны с энергией Е_п в результате вза­имодействия с тканеэквивалентным веществом создают в элементе объема этого вещества заряженные частицы с различными энер­гиями. В равновесном состоянии устанавливается спектр замедле­ния (см. § 83), который и определяет реальное распределение ча­стиц по ЛПЭ. Следовательно, коэффициент качества моноэнерге­тических нейтронов — это усредненный по спектру замедления ко­эффициент качества вторичных заряженных частиц, которые и формируют поглощенную дозу. Обозначим этот коэффициент ка­чества к (Е_п). На рис. 103 (кривая 1) показана зависимость к(Е_п) от энергии нейтронов.

Фактор эквивалентной дозы — это переводной коэффициент, связывающий флюенс в некоторой точке исходного радиационного поля с эквивалентной дозой Н в элементе объема тканеэквивалент­ного вещества, помещенном в эту же точку. Для моноэнергетиче­ских нейтронов с энергией Е_п

Н (Е_п)=Ь (Е_п) Ф (Е_п) ٠ (П2.5)

где Н(Е_п)—зависящий от энергии нейтронов фактор эквивалент­ной дозы. В условиях энергетического равновесия устанавливает­ся простая связь между величинами Н(Е_п), /г(Е_п) и к(Е_п);

Ь(Еп)-=к(Е_пУк(Е_п). (П2.6)

374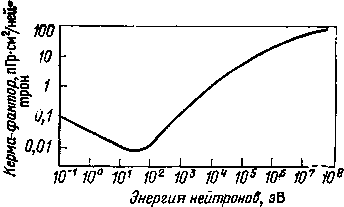

- ٧ /

Рис. 104. Изменение фантомно-зависимо- го переводного коэффициента с(£٦) от энергии фотонов £٢ для тканеэквива- ٠ лентного шара диаметром 30 см ٠5۶؛ ٦٠

1,0 ؟

Все рассмотренные коэффици- ٦١ енты являются базисными величи- нами. Теперь перейдем к фантом- ،٥ ٥₂

но-зависимым переводным коэф- ’ ٥

фициентам. К ним мы отнесем ٢^{2 10}'^{1 10}° ¹°¹

такие, которые переводят дозимет- Энергия фотонов> МэВ

рическую величину любого класса в фантомно-зависимую. Пусть, например, нас интересует значение эквивалентной дозы Н(Е_У) в некоторой точке внутри фантома, который помещен в исходное поле моноэнергетического фотонного излучения с заданным зна- чением экспозиционной дозы X. Экспозиционная доза в данном случае является базисной величиной и относится к заданной точ- ке невозмущенного радиационного поля. Связь между этими двумя величинами может быть записана через переводной коэффициент с(£_?), который зависит от энергии фотонов и параметров фантома:

Н(Е_у)=с(Еу)Х, (П2.7)

где с(Еу)—фантомно-зависимый переводной коэффициент. На рис. 104 показана энергетическая зависимость этого коэффициента для тканеэквивалентного шара диаметром 30 см, помещенного в мононаправленный параллельный пучок фотонов; при этом экви* валентная доза Н(Е_У) относится к точке на глубине 10 мм по диа- метру шара в направлении распространения излучения.

Рассмотрим теперь переводной коэффициент для преобразова- ния фантомно-зависимой поглощенной дозы нейтронного излуче- ния в фантомно-зависимую эквивалентную дозу. Поглощенная и эквивалентная дозы в элементе объема внутри фантома форми- руются нерассеянными нейтронами, рассеянными нейтронами, а также фотонным излучением, возникающим при взаимодействии нейтронов с веществом фантома.

Пусть Ф(£_п)—энергетический спектр, а к(Е_п) — керма-фак- тор нейтронов в некоторой точке внутри тканеэквивалентного фан- тома, находящегося в однородном поле моноэнергетических ней- тронов с энергией £٠٠ Тогда доза излучения И (£₀) — поглощенная доза в данной точке фантома может быть выражена следующей формулой:

؛ = (٥£) ٥ Ф (£„) к (Е_п) <1Е_п + ٥٦ (£₀). (П2.8)

Соответственно эквивалентная доза

н (٠ (٤٠ 1 Ф (٤„) к (Е_п) к(Е_п) аЕ_п + ٠(٥£)٥٦

(П2٠9١

375