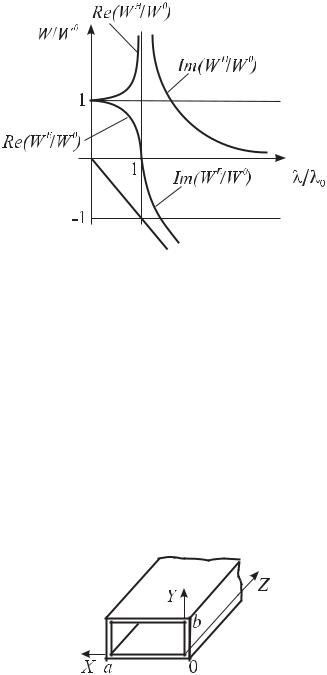
Рис. 6.23.

В обоих случаях поток энергии имеет чисто реактивный характер.

6.7.Электрические (Е) типы волн в прямоугольном волноводе

Для решения краевой задачи в прямоугольной области воспользуемся прямоугольной системой координат и сориентируем её так относительно конфигурации волновода, как показано на рис. 6.24. Размер широкой стенки

– a, узкой – b.

Рис. 6.24.

Краевая задача для собственной функции ψe в рассматриваемом случае имеет вид

59

Поскольку слева и справа в (6.26) разные переменные, обе эти части могут быть при выполнении равенства только константой, которая обозначе-

на как 2y . Эта константа имеет смысл постоянной разделения. Положим также v2 −2y = 2x . Тогда получим из двойного равенства (6.26) два уравнения:

(A2 cos( y y)+ B2 sin ( y y)).

Используя граничные условия (6.24), получаем

Критическая длина волны λemn при этом рассчитывается как

60

моугольных волноводах при низших индексах.

1. Наибольшая критическая длина волны оказывается у Е11-волны:

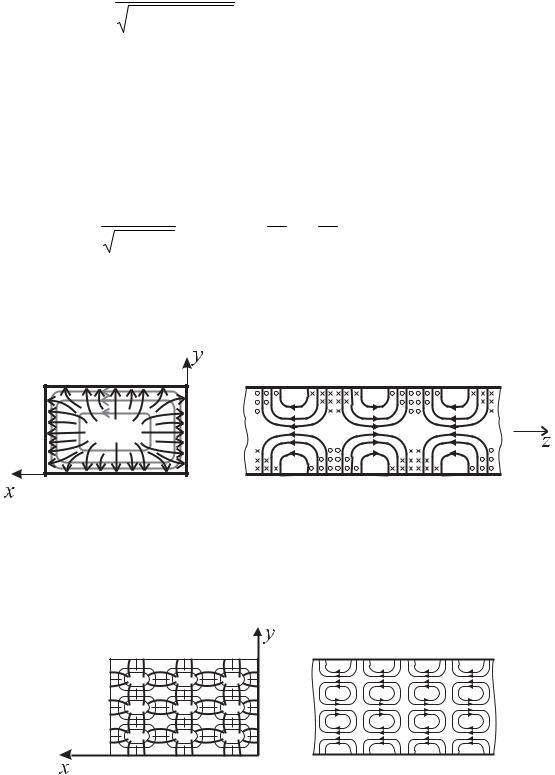
Используя рельеф ψ11e , получаем структуру поля волны Е11 в поперечном и продольном сечениях волновода, изображенную на Рис.6.25 (сплош-

Рис. 6.25.

ные линии напряженности E , штриховые - H ).

2. При увеличении индексов m и n картина поля Е11 мультиплицируется m раз по Х и n раз по Y. Для примера на Рис.6.26 изображена структура поля

Е33.

Рис. 6.26.

6.8. Магнитные волны в прямоугольном волноводе

Краевая задача для ψvm имеет вид

61

Используя, как и ранее, метод разделения переменных, получаем общее решение (17.1) в виде

ψvm = (A1 cos( x x)+ B1 sin( x x))(A2 cos( y y)+ B2 sin( y y)).

Применяя граничные условия (17.2), имеем

Построим структуру полей Н-волн в прямоугольном волноводе, используя установленные выше правила: поперечное распределение Нz совпа-

дает c ψmnm (x, y), линии Ertmn совпадают с линиями уровня ψmnm , линии Htmn соответствуют gradψmnm .

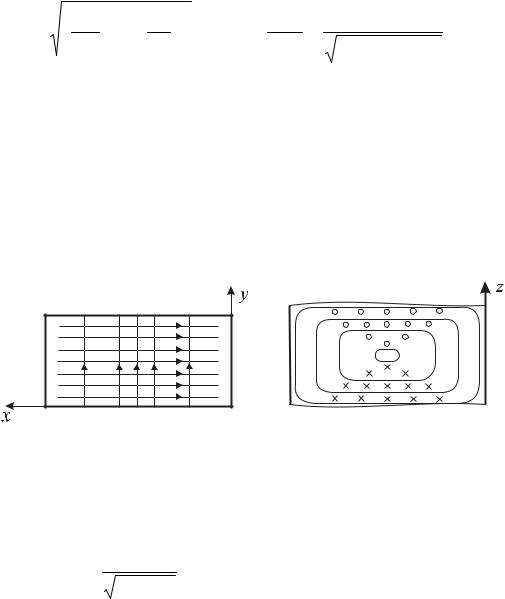
1. При a>b наибольшей критической длиной волны λmmn обладает волна H10 = λ10m = 2a . Распределение силовых линий волны представлено на

рис. 6.27.

Рис. 6.27.

2. Волна Н01 имеет критическую длину волны λm01 = 2b . Её структура изображена на Рис.6.28, она аналогична структуре волны Н10, но развернута на 90° относительно плоскости XZ.

3. На Рис.6.29 изображена поперечная структура волны Н11. Её крити-

ческая длина λm = 2ab .

11 a2 + b2

62

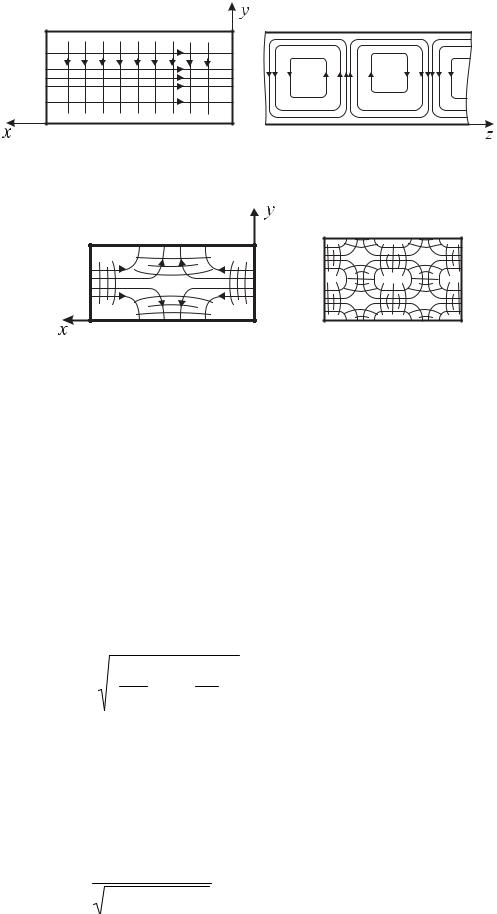
Рис. 6.28.

Рис. 6.29. Рис. 6.30.

4. Поперечная структура волны Н22 изображена на Рис.6.30. Она представляет собой двухкратную мультипликацию структуры волны Н11 в Х- и Y- направлениях.

6.9. Вырождение волн в прямоугольном волноводе. Доминантная волна и рабочий диапазон прямоугольного волновода

Как указывалось раньше, случай, когда одному собственному значениюv соответствует две и более различных собственных функций ψv , называ-

ется вырождением. Для прямоугольного волновода при ненулевых индексах m и n имеет место именно такой случай:

т.е. граничные условия первого рода (6.24) и второго рода (6.30) дают одинаковые собственные значения. При этом ψmne и ψmnm различны. С технической точки зрения существенно, что критические длины волны λemn и λmmn одинаковы:

63

Вследствие этого и дисперсионные зависимости постоянных распространения волн Нmn и Emn одинаковы:

Таким образом, можно говорить о ЕН волнах, хотя возможно раздельное возбуждение Emn и Нmn волн ввиду различия структуры полей этих волн. Однако существующие в реальных устройствах неоднородности (специальные или случайные) приведут к преобразованию Emn волн в Нmn и наоборот. Благодаря одинаковым фазовым скоростям эти преобразования будут иметь кумулятивный характер.

При конструировании СВЧ-устройств рабочий диапазон волновода следует выбирать так, чтобы в нем распространялась только одна волна, другие же были закритическими. В качестве такой волны волновода должна быть выбрана доминантная (основная) волна волновода с наибольшей критической длиной волны. В случае a>b в прямоугольном волноводе такой волной является волна Н10. Если a>2b (что выполняется для всех стандартных конфигураций прямоугольного волновода), то ближайшей мешающей (пара-

зитной) волной будет Н20. Следовательно, в диапазоне λ10H = 2a < λ < λH20 = a может распространятся только доминантная волна Н10. Рабочий диапазон, однако, меньше октавы: вблизи λ=2а слишком сильна дисперсия и связанные с ней фазовые искажения сигналов и критичность настроек, вблизи λ=а усиливается реактивность, связанная с высшими типами волн и возникает опасность паразитной связи между элементами тракта на этих волнах, которые становятся слабо закритическими и медленно затухают вдоль оси волновода.

6.10.Электрические (Е) волны в волноводах

скруговыми сечением

Воспользуемся цилиндрической системой координат, как это показано на рис.6.32.

Рис. 6.32.

64

Краевая задача для функции ψve (r, ϕ) в рассматриваемом случае имеет

вид

Таким образом, уравнения (6.32) в системе координат r, ϕ записываются как

Воспользуемся методом разделения переменных и представим искомые решения ψve = R(r) Φ(ϕ). Подставляя его в (6.34), получаем

Здесь λ2 - постоянная разделения. Запишем уравнения для Ф:

d 2Φ + λ2Φ = 0 . dϕ 2

Решение этого уравнения имеет вид

Φ = cos(λϕ +α).

65

Поскольку условие замкнутости по ϕ требует

Φ(ϕ)= Φ(ϕ + 2π ),

заключаем, что λ=n, n=0,1,2,... .

Для краткости записи положим также постоянную отсчета по ϕ α=0. Таким образом, частное решение для Ф запишем как Фn(ϕ)=cos nϕ .

Уравнение для R теперь имеет вид

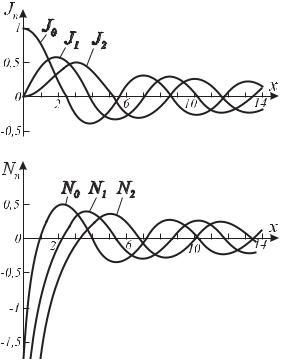
Уравнение (6.36) представляет собой известное уравнение Бесселя, имеющее в качестве решений функции Бесселя первого рода n-го порядка Jn( n r) и функции Бесселя второго рода n-го порядка Nn( n r) (функции Неймана). На Рис.6.33 представлен характер зависимостей Jn( n r) и Nn( n r).

Рис. 6.33.

Очевидно, что поскольку Nn( n r)→ - ∞ при r→ 0, эти функции должны быть исключены из решения, поскольку ψne при r→ 0 не должна обращаться в бесконечность. Таким образом, Rn= Jn( n r) и соответственно

ψne = J n ( n r)cos nϕ .

Используем теперь граничное условие (6.33):

66

J n ( n a)= 0 .

Обозначим v ni i-й корень функции Бесселя Jn (x) : Jn (vni)=0. Тогда eni a = vni

а собственная функция имеет следующую форму:

Используя (6.39) и правила изображения поля, проанализируем структуру некоторых типов Е-волн.

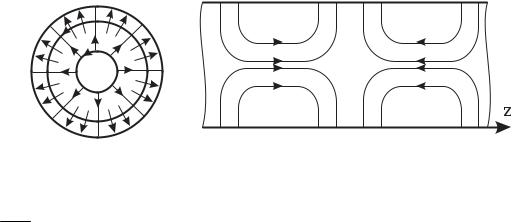
1. Структура волны E01 в поперечном и продольном сечениях изображена на рис.6.34.

Рис. 6.34.

Это основная волна типа Е с наибольшей критической длинной волны

λe = 2πa . Первый нулевой индекс указывает, что волна азимутально-

01 v01

симметричная.

2. Волна Е11 – несимметричная. Её структура в поперечном и продольном сечениях изображена на рис.6.35.

67