
- •ЭЛЕКТРОДИНАМИКА И РАСПРОСТРАНЕНИЕ РАДИОВОЛН
- •ПРЕДИСЛОВИЕ
- •1.1. Интегральная формулировка УМ
- •1.3. Физическое содержание первого УМ
- •2.1. ГУ для тангенциальных составляющих векторов ЭМП
- •2.2. ГУ для нормальных составляющих векторов ЭМП
- •3.2. Баланс энергии в ЭМП. Теорема Умова-Пойтинга
- •4.2. Теорема о комплексной мощности
- •5.2. Электродинамические потенциалы
- •6.4. Общие свойства магнитных (Н) волн
- •6.7. Электрические (Е) типы волн в прямоугольном волноводе
- •6.8. Магнитные волны в прямоугольном волноводе
- •6.11. Магнитные (Н) волны в круглом волноводе
- •6.12. Потери и затухание волн в волноводах
- •7.3. Уравнения возбуждения регулярных волноводов сторонними токами
- •8.1. Неортогональные координатные системы
- •8.2. Дифференциальные операторы
- •8.4. Уравнение возбуждения произвольно-нерегулярного волновода сторонними токами
- •8.5. Самосогласованные нелинейные уравнения лампы бегущей волны О - типа
- •8.6. Уравнения возбуждения произвольно-нерегулярного коаксиального волновода
- •8.7. Уравнения возбуждения нерегулярных замедляющих систем
- •8.8. Нерегулярные волноводы с прямоугольным сечением.
- •8.9 Т-функции для решения двухточечных задач в теории нерегулярных волноводов
- •8.9.1 Т-функции
- •8.9.2 Взаимодействие Hoi волн в гофрированном волноводе с круговым сечением
- •9.3. Трансформирующие свойства отрезков линий передачи.
- •9.4. Короткозамкнутые и разомкнутые на конце отрезки линии передачи (шлейфы).
- •9.5. Частичное отражение волн в линиях передачи.
- •10.1. Понятие планарных линий передачи.
- •10.2. Симметричная полосковая линия
- •10.3. Несимметричная полосковая линия
- •10.4. Симметричная щелевая линия
- •10.5. Несимметричная щелевая линия
- •10.6.1 Общая формулировка метода
- •10.7. Копланарная линия передачи
- •10.8. Четная и нечетная моды в связанных полосковых линиях
- •11.2 Поля в ОР как в отрезках регулярных волноводов с короткозамыкающими крышками
- •11.3 Расчет полей в резонаторах с помощью потенциалов Герца
- •11.3.1 Прямоугольный резонатор
- •11.3.2. Цилиндрический резонатор
- •11.4 Добротность собственных колебаний в резонаторах. Внешняя и нагруженная добротности
- •12.2 Свойства собственных функций резонатора
- •12.3 Уравнение возбуждения резонатора
- •12.4. Способы возбуждения резонаторов
- •13.1. Расчет полей с помощью электрического вектора Герца
- •13.2. Анализ поля ЭЭИ в квазистатической (ближней) зоне
- •13.3. Анализ поля ЭЭИ в волновой (дальней) зоне
- •14.3. Анализ поля ЭМИ в волновой (дальней) зоне
- •18.2. Зоны Френеля. Область, существенная для распространения радиоволн
- •18.3. Дифракция электромагнитных волн от края непрозрачного экрана
- •19.2. Наклонное падение горизонтально-поляризованной волны на плоскую границу раздела двух сред
- •19.3. Наклонное падение вертикально-поляризованной волны на плоскую границу раздела двух сред
- •19.4. Отражение плоских волн от плоской границы среды с потерями
- •20.3. Поле вертикального вибратора над плоской отражающей поверхностью
- •20.4. Поле горизонтального вибратора, поднятого над плоской поверхностью земли на высоту h
- •20.7. Учет сферичности земной поверхности
- •20.9. Дифракция радиоволн вокруг сферической земной поверхности
- •21.2. Поглощение радиоволн в тропосфере
- •21.3. Рефракция радиоволн в тропосфере
- •22.2. Механизм ионизации и рекомбинации на больших высотах
- •22.3. Электронная диэлектрическая проницаемость ионизированного газа без учета столкновений электронов с ионами и нейтральными молекулами
- •22.5. Преломление и отражение радиоволн в ионосфере
- •22.6. Влияние магнитного поля Земли на распространение волн в ионосфере. Двойное лучепреломление
- •23.1 Уравнения движения электрона в форме Лагранжа.
- •23.2 Поступательная (трансляционная) симметрия
- •23.3. Азимутальная симметрия
- •23.4. Вращающиеся поля
- •23.5. Бегущие в направлении z волны
14.2. Анализ поля ЭМИ в квазистатической (ближней) зоне
Рассмотрим случай kr<<1, e− jkr ≈1. В таком пределе получаем из
(14.3)
|
|
&cт |
µa |
|
sinθ |
|
|
E& |
= − |
jωSI |
|
. |
(14.6) |
||
|
|
|
|||||
ϕ |
|
4π |
|
|
r 2 |
|
|
|
|
|
|
|
|||
Формула (14.6) выражает квазистатическую часть E& |
рамки с током |
||||||
|
|
|
|
|
|
ϕ |
|
I&m .
Выделяя таким же образом главные (по величине) члены в (14.4) и (14.5), имеем:
& |
&cт |
cosθ |
|
& |
&cт |
sinθ |
|
|
SI |
, |
SI |
. |
(14.7) |
||||
Hr = |
2π |
r3 |
Hθ = |
4π |
r3 |
|||
|
|
|
|
|
Поля (14.7) представляют собой квазистатическую часть полного магнитного поля ЭМИ и соответствуют стационарному полю магнитного диполя.
Существенно отметить, что поля |
E& |
(14.6) и H& |
r |
, |
H& |
0 |
(14.7) сдвинуты по |
||
|
|
ϕ |
|
|
|
|
|
||
фазе на π/2 ( E& |
|
− j |
π |
|
|
|
|
|
|
имеет множитель − j = e |
|
2 ), т.е. это поля – чисто реактив- |
|||||||
ϕ |
|
|
|
|
|
|
|
|
|
ные и к полю излучения отношения не имеют.
14.3. Анализ поля ЭМИ в волновой (дальней) зоне
Рассмотрим теперь противоположный случай, когда kr>>1 и поле приобретает волновой характер. Главные по величине составляющие поля ЭМИ теперь имеют следующий вид:
E& |
|
|
&cт |
µak e |
− jkr |
|
|
|
|
||||||
|
= ωSI |
|
|
sinθ , |
|
|
(14.8) |
||||||||
ϕ |
|
4π |
|
|
|
|
|
r |
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
H& |
|
|
&cт |
|
2 |
|
− jkr |
|
|
|
|
|
|||
θ = − SI |
|
|
k |
|
e |
r |
sinθ . |
|
|
(14.9) |
|||||
|
|
|
4π |
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
&cт |
k |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
& |
SI |
|
|
|
Введем комплексную амплитуду магнитного поля A = |
4π |
|
|
. Тогда |
|||||||||||
& |
|
& |
|
0 e j(ωt −kr) |
sinθ , |
|
|
(14.10) |
|||||||
Eϕ = AmW |
|
|
|
|
r |
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
225

& |
& |
e j(ωt −kr) |
sinθ . |
(14.11) |
Hθ = −Am |
r |
|||
|
|
|
|
|
Анализ формул (14.10), (14.11) приводит к выводам того же характера, что и при анализе полей в волновой зоне ЭЭИ:
1) поля Е и Н синфазны и образуют структуру сферической волны, распространяющейся в направлении r0 от источника с фазовой скоростью
vф = ω / k =1/  εa µa ;
εa µa ;
2)в пространстве без потерь Е и Н убывают пропорционально 1/r;
3)излучение ЭМИ неизотропно, диаграмма направленности F(θ)=sinθ;
4) отношение E& и H& равно волновому сопротивлению W 0 = µa /εa . Составим вектор Пойнтинга для поля излучения ЭМИ (14.10), (14.11):
r& |
|
1 |
r& r& |
1 |
r |
|
r |
& &* |
r |
Im2 |
π 2 |
( S / |
λ2 )2W 0 |
sin |
2 |
|
|
||||
S |
0 |
= |
|
[ E,H*] = − |
|
[ϕ |
0 |
,θ |
0 |
] E |
H |
θ |
= r |
|
|
|
|
|
θ . |
(14.12) |
|
|
|
2 |
|
2 |
|
|
ϕ |
|
0 |
|
|
2r |
2 |
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
Как и в случае ЭЭИ для подсчета полной мощности излучения ЭМИ, найдем поток Re Sr&0 через сферу радиуса r с центром в точке расположения ЭМИ. Тогда получим
r& |
r |
= |
Im2π 2 ( S / |
λ2 )2W 0 π 2π |
3 |
θdϕdθ = |
|
P∑ = Re ∫S0 ds |
2 |
∫ ∫ sin |
|
|
|||
s |
|
|
0 0 |
|
. |
(14.13) |
|
|
|
|
|
||||
= 43 π 3 ( S / λ2 )2 Im2W 0
Вводя, как и ранее, сопротивление излучения RΣ рамки с током Iст, получаем
P = |
4 |
π |
3 |
|
2 |
|
2 |
I |
2 |
W |
0 |
= |
1 |
I |
2 |
R , |
|||||
3 |
|
(S / λ ) |
|
|
|
|
2 |
|
|||||||||||||
∑ |
|
|
|
|
|
|
|
|
|
|
m |
|
|
|
|
|
m ∑ |
||||
R = |
8 |
π |
3 |
2 |
) |
2 |
W |
0 |
. |
|
|
|
|
|
(14.14) |
||||||
|
|
|
|
(S / λ |
|
|
|
|
|
|
|
|
|||||||||
∑ |
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
В случае возбуждения волны в атмосфере или пустоте W 0 =120π [Ом]
и
P = 320π 4 |
(S / λ2 )2 |
[Ом}. |
(14.15) |
∑ |
|
|
|
226
ГЛАВА XV
ЭКВИВАЛЕНТНЫЕ ИСТОЧНИКИ ЭЛЕКТРОМАГНИТНОГО ПОЛЯ
При расчете электромагнитных полей часто удобно прибегать к декомпозиции задачи: сложный исследуемый электродинамический объект подразделяется на независимо анализируемые части, или автономные блоки. Эти блоки разделяются некоторыми заданными поверхностями, на которых задаются эквивалентные граничные условия, которые позволяют после решения краевой задачи для автономных блоков синтезировать решение общей (исходной) задачи. Один из способов согласования решений в отдельных подобластях - введение системы эквивалентных источников на граничных поверхностях. Например, стоит задача расчета поля излучения рупорной антенны (или рупорного облучателя антенны). Очевидно, задача возбуждения ЭМП от заданного распределения сторонних источников в рупоре является самостоятельной, довольно детально разработанной задачей. Поэтому можно
считать, что поле Er0 , Hr 0 на плоскости S раскрыва рупора известно (можно ввести в качестве границы не плоскость, а, например, участок сферической или эллипсоидальной поверхности, если это повышает точность представления граничных полей). Тогда для расчета поля излучения рупора удобно ввести на S эквивалентные источники ЭМП, определяемые через значения
Er0 , Hr 0 на S по следующей схеме.
Если заменить поверхность раскрыва рупора идеально проводящей по-
верхностью, то для задания на этой поверхности H 0 следует в соответствии с известными граничными условиями (глава, первая часть курса) ввести экви-
валентную поверхностную плотность тока δse :
r |
r r |
, |
(15.1) |
δse =[n, H 0 ]/s |
|||
nr - внешняя нормальr к S.
Для замены E0 следует ввести на S эквивалентную поверхностную плотность магнитного тока δsm , используя свойство перестановочной двойственности уравнений Максвелла:
δrsm = −[nr, E0 ]/s . |
(15.2) |
С другой стороны, для гармонических источников имеем:
r&e |
|
r |
rcm |
|
|
|
∂pcm |
|
|||
|
|
|
& |
|
|
δs |
= |
|
= jωp , |
(15.3) |
|
∂t |
|||||
|
|
|
|
227
r&m |
|
∂Jrcm |
|
|
|
|
|
|
r&cm |
|
|
|
||||||||||
δs = |
|
|
|
|
|
|
|
= jωJ |
. |
|
(15.4) |
|||||||||||
|
∂t |
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
rcm |
|
|
|
r&cm |
|
|
|
|
|
|
|
|
|
|
|
|||||||
& |
|
|
|
|
и J |
|
|
|
соответственно сторонние поляризованность и намагничен- |
|||||||||||||
Здесь p |
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
rcm |
r&cm |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
& |
J эквивалентных источни- |
|
ность на S. Таким образом, на S заданы p и |
||||||||||||||||||||||
ков следующим образом: |
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
r |
|
|
r |
0 ] |
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
rcm |
|
|
|
|
|
[n, H |
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
& |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
p |
|
|
s |
= |
|
|
|
jω |
|
|
|
s |
, |
|
|
(15.5) |
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
r |
r |
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
0 ] |
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
r |
|
|
|
|
|
|
[n, E |
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|||||||||||||
J&cm |
|
s |
|
= − |
|
|
|
|
|
|
|
|
|
. |
|
|
(15.6) |
|||||
|
|
|
|
jω |
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
s |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Теперь можно использовать решения для из главы XIII данной части курса:
r& l |
|
|
1 |
|
|
|
|
|
|
r |
r& |
0 |
]e |
− jkr |
ds |
|
||||
(A) = |
|
|
|
∫∫ |
[n, H |
|
|
|
|
|||||||||||
Π |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
, |
||||
4π jωε |
a |
|
|
|
|
r |
|
|
|
|
|
|||||||||
|
|
|
|
|
|
s |
|
|
|
|
|
|
|
|
|
|
|
|||
r& m |
|
|
−1 |
|
|
|
|
|
|
r |
r& |
0 |
]e |
− jkr |
ds |
|
||||
(A) = |
|
|
|
|
|
∫∫ |
[n, E |
|
|
|
|
|||||||||
Π |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
. |
||||
|
|
4π jωµ |
a |
|
|
|
|
r |
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
s |
|
|
|
|
|
|
|
|
|
|
|
||
Πr& l ( A) и Πr& m ( A) типа (13.2)
(15.7)
(15.8)
Здесь r – расстояние от элемента поверхности ds до точки наблюдения А. Используя известные формулы связи E, H с Πr l и Πr m (cм. Главу V
первой части), получаем следующие общие выражения для полей излучения исследуемой антенны:
r |
r |
r |
r |
|
E& |
= k2Πl + graddivΠl − jωµarotΠm , |
(15.9) |
||
r |
r |
r |
r |
|
H& |
= k2Πm + graddivΠm + jωεarotΠl . |
(15.10) |
||
Дифференцирование в (15.9), (15.10) производится по координатам точки наблюдения А.
228
ГЛАВА XVI
ПЛОСКИЕ ЭЛЕКТРОМАГНИТНЫЕ ВОЛНЫ
16.1. Определение плоских электромагнитных волн
rПлоскими называются электромагнитные волны, в которых векторы Е
иН нормальны к направлению распространения z, зависят только от z и не
зависят от поперечных к z координат q1, q2 (x, y, например).
Между тем, как следует из материалов глав XIII, XIV, поля элементарных источников в волновой зоне представляют собой сферические волны, расходящиеся от источников в свободном пространстве.
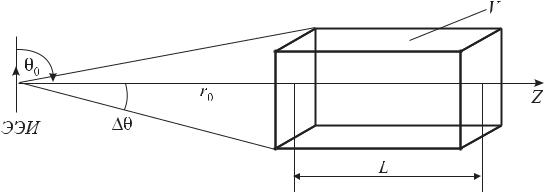
Плоскую волну можно рассматривать как некоторое приближение структуры сферической волны в конечном объеме, достаточно удаленном от источника. Геометрические характеристики такого объема V представлены на рис. 16.1.
Рис. 16.1.
Для определенности рассмотрим электромагнитное поле элементарного электрического излучателя (ЭЭИ), расположенного при r=0 в сферической системе координат r,θ ,ϕ , как это указано на рис. 16.1. Рассматриваемый ко-
нечный объем V расположен на расстоянии r0 от источника, внутри V r=r0+z, угловое расхождение по максимальным поперечным размерам V равно ∆θ . Поля источника в области V в сферической системе координат, как было установлено в главе XIII, для волновой зоны могут быть записаны как
E&θ = A&W 0e− jkr sinθ / r,
(16.1)
H&ϕ = A&e− jkr sinθ / r
Положим теперь, что поперечные размеры V настолько ограничены,
что ∆θ → 0 , а удаление V от источника настолько велико (а длина его L на-
θ0
229
столько ограничена), что L<<r0. Но в то же время будем предполагать, что L>> λ , т.е. kz – величина большая.
При указанных условиях
sinθ |
≈ |
sinθ0 |
, kr = kr + kz |
(16.2) |
|
|
|||
r |
0 |
|
||
|
r0 |
|
||
Используя приближение (16.2) в формулах (16.1), положим
& e− jkr0 |
& |
jωt |
(16.3) |
|
A |
r0 |
sinθ0 = A0 e |
|
|
|
|
|
|
|
При обозначении (16.3) с учетом (16.2) из (16.1) получаем следующее приближение для V:
E&θ = A&W 0e j( ωt−kz ) ,
(16.4)
H&ϕ = A&e j( ωt−kz )
В дальнейшем для описания плоских волн в V удобно ввести прямоугольную систему координат и переобозначить в (16.4): Е&θ = Е&Х , Н&ϕ = Н&У .
Тогда мы приходим к обычной записи компонент плоской волны в координа-
тах x, y, z:
E&Х = A0W 0e j( ωt−kz ) ,
(16.5)
H&У = A0e j( ωt−kz )
Поля Е&Х , Н&У , определяемые формулами (16.5) полностью соответст-
вуют определению плоской волны с амплитудой А0.
Нетрудно убедиться прямой подстановкой решений (16.5) в уравнения Максвелла, что они этим уравнениям удовлетворяют, т.е. приближение плоской волны вполне реально.
16.2. Плоские волны в однородной изотропной среде без потерь. Поляризация плоских волн
В рассматриваемом случае электрические и магнитные параметры среды εа и µа - действительные, постоянные (не зависящие от координат) и
скалярные (не тензоры) величины. Поэтому волновое число k имеет только фазовую постоянную β , постоянная затухания α равна нулю:
230

k = ω εa µa |
= β = |
ω = |
2π |
, |
|
|
|
|
υcp |
λ |
|
|
|
|
|
|
(16.6) |
υcp = |
1 |
, λ =υcpT = |
T |
||
|
εa µa |
|
|
εa µa |
|
Запишем теперь (16.5) в векторной форме
Er& = xr0 A0W 0 e j( ωt−kz )
(16.7)
Hr& = yr0 A0 e j( ωt−kz )
Формулы (16.7) определяют плоскую волну, вектор E в которой при любых t, z колеблется в плоскости xz. Такая волна называется линейно поля-
ризованной, а плоскость, в которой расположен вектор E (в рассматриваемом случае – плоскость xz) называется плоскостью поляризации плоской электромагнитной волны. При распространении волны у земной поверхности
плоскости поляризации обычно называют горизонтальной (вектор E параллелен горизонту) и вертикальной, если плоскость поляризации нормальна горизонту. В дальнейшем будем придерживаться такой терминологии.
В общем случае плоская волна представляет собой суперпозицию волн вертикальной и горизонтальной поляризаций:
r& |
r |
& |
− jkz |
r |
& |
− j( kz+α ) |
(16.8) |
Е = x0 АВе |
|
+ y0 AΓ e |
|
||||
& |
|
0 |
jωt |
|
|
|
|
= ABe |
|
- комплексная амплитуда вертикально поляризованной |
|||||
Здесь AB |
|
||||||
волны, А&Г |
= АГ0 еjωt |
- комплексная амплитуда горизонтально поляризованной |
|||||
волны, α - сдвиг фазы горизонтально поляризованной волны относительно вертикально поляризованной.
Рассмотрим некоторые типичные случаи.
а) Амплитуды волн различны: АВ0 ≠ АГ0 , сдвиг фаз отсутствует: α =0.
В этом случае суммарная волна линейно поляризованная, ее плоскость поляризации отклонена от вертикальной плоскости xz на постоянный угол υ ,
A0
который определяется как tgυ = Γ = const .
AB0
Амплитуда суммарного поля А0 =  (АВ0 )2 + (АГ0 )2 .
(АВ0 )2 + (АГ0 )2 .
231

б) Амплитуды волн одинаковы: АВ0 = АГ0 = А0 ,α = π 2 . В этом случае из (16.8) следует:
Еr& = А0 (хr0 − jyr0 )e j( ωt−kz ) .
Перейдем к действительным величинам
Er = Re Er& = A0 xr0 cos(ωt − kz)+ yr0 sin(ωt − kz) = xr0 EB (t, z)+ yr0EΓ (t, z),
EB (t,z)= A0 cos(ωt − kz), EΓ = A0 sin(ωt − kz).
Теперь угол отклонения вектора E суммарной волны определяется как
υ = arctg EΓ ( t,z ) =ωt − kz . EB ( t,z )
Такимr образом, если зафиксировать t=t0=const (мгновенная картина), вектор E располагается на винтовой поверхности, определяемой вращением угла υ по закону: υ = −kz +ωt0 . Если же зафиксировать плоскость
z=z0=const, то в этой плоскости вектор E вращается с частотой ω по закону: υ =ωt − kz0 . Причем, амплитуда E остается постоянной и равной А0.
В тройке векторов x0 , y0 , z0 вращение происходит против часовой
стрелки (по закону правой тройки) и поэтому волна описанного типа называется правополяризованной волной с круговой поляризацией (поскольку А0=const).
в) Амплитуды волн одинаковы: АВ0 = АГ0 = А0 ,α = −π 2 . В этом случае
2 . В этом случае
EB ( t,z ) = A0 cos(ωt − kz), EΓ ( t,z ) = −A0 sin(ωt − kz). Соответственно υ( t,z ) =
= −(ωt − kz). Это тоже волна с круговой поляризацией, но левополяризован-
ная в отличие от предыдущей, поскольку вращение вектора E в ней происходит в противоположном направлении.
Нетрудно убедиться, что любую линейно-поляризованную волну с амплитудой А0 можно представить как суперпозицию двух лево- и правополяризованных волн с одинаковой амплитудой А0/2. Такое представление весьма полезно при анализе распространения линейно поляризованных волн в анизотропных средах (например, в намагниченных плазме или феррите). Дело в том, что взаимодействие лево- и правополяризованных волн с анизотропной средой существенно различается и разложение линейно поляризованной волны на две указанные составляющие весьма полезно при анализе взаимодействия.
232
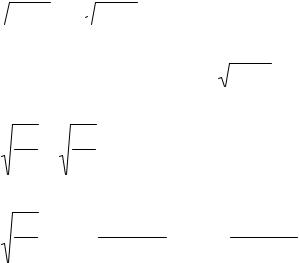
В общем случае А0 |
≠ А0 |
и α ≠ ±π |
. При этом вращение вектора E |
В |
Г |
2 |
r |
|
|
также происходят с угловой частотой ω , но амплитуда вектора E зависит от
угла υ , т.е. конец вектора E «описывает» не круг, а эллипс. Поэтому в общем случае волна имеет ни линейную, ни круговую, а эллиптическую поляризацию.
16.3. Плоские волны в среде с потерями
Если свободное пространство однородно и изотропно, но имеются диэлектрические, джоулевы и магнитные потери, то параметры среды εа и µа -
комплексные. Представим их в показательной форме:
& |
= εаe |
− j∆E |
& |
= µa e |
− j∆H |
(16.9) |
|
εа |
|
, µa |
|
||||
Здесь εa , µa |
- модули соответствующих величин; ∆Е , ∆Н |
- угол соответст- |
|||||
венно электрических и магнитных потерь.
Теперь как волновое число, так и волновое сопротивление пространства – комплексные величины. Запишем их в следующей форме:
k& = ω ε&a µ&a = ω
ε&a µ&a = ω  εa µa e− jθ1 = β − jα,
εa µa e− jθ1 = β − jα,
β = k cosθ1 , |
β = k sinθ1 , |
|
|
k = ω |
εa µa |
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(16.10) |
& |
0 |
|
|
µ&a |
|
µa |
|
|
jθ |
2 |
|
|
|
0 |
|
jθ |
2 |
|
|
||||
|
= ε&a |
|
εa e |
|
|
|
|
|
|
|
|
|
|
||||||||||
W |
|
= |
|
|
|
=W e |
|
|
, |
|
|||||||||||||
W 0 = |
|
µa , θ1 = |
∆E + ∆H |
|
, θ2 = |
∆E − ∆H . |
|||||||||||||||||
|
|
|
|
εa |
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
2 |
|||
Теперь компоненты E, H плоской волны могут быть представлены как |
|||||||||||||||||||||||
r& |
|
r |
|
|
0 |
A e |
j( ωt−βz+θ |
2 |
) |
e |
−αz |
, |
|
|
|
|
|||||||
E |
= x W |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
0 |
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
r& |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(16.11) |
|
r |
A e |
j( ωt−βz ) |
e |
−αz |
|
|
|
|
|
|
|
|
|
|
||||||||
H = y |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
0 |
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Таким образом, в среде с потерями, как следует из (16.11), имеют место два эффекта.
233
1.Напряженности поля Е, Н убывают в направлении распространения экспоненциально с постоянной затухания α .
2.Вектор Еr& имеет фазовый сдвиг относительно Нr& величиной θ2 . Это, между прочим, означает, что на периодических интервалах по z длиной
∆z = |
θ2λ |
( λ = 2π / k cosθ1 ) в связи со сменой ориентации Еr относительно |
|
|
|
2π |
|
Нr |
вектор Умова-Пойнтинга S0 = [E,H ] меняет знак на обратный. Иначе го- |
||
воря, на указанных интервалах поток энергии в волне в заданный момент t=t0=const противоположен направлению распространения волны, что представляется весьма интересным с точки зрения физики распространения радиоволн.
К ним следует добавить еще и третий эффект: поскольку в средах с потерями ∆Е и ∆Н зависят от частоты, в таких средах имеет место дисперсия, т.е. зависимость β, α, W0 от частоты.
234

ЧАСТЬ 5
РАСПРОСТРАНЕНИЕ ЭЛЕКТРОМАГНИТНЫХ ВОЛН В ПРИРОДНЫХ УСЛОВИЯХ
ГЛАВА XVII
ДИАПАЗОНЫ ВОЛН. КЛАССИФИКАЦИЯ РАДИОВОЛН ПО МЕХАНИЗМУ РАСПРОСТРАНЕНИЯ
Как указывалось в первой части курса, мы рассматриваем классическую теорию электромагнитных явлений, в которой дискретность вещества (среды) и излучения не учитывается, а поле предполагается континуальным. Такие представления ограничивают спектр волн, где классическая теория еще применима; если рассматривать мощности > I мкВт, то границей частот, выше которой заметно проявляется дискретность излучения, будет fгр ~3 1012 . Весь спектр частот f < fгр может быть разбит на диапазоны. В нашей стране принято следующее разделение радиоволн по диапазонам:
Сверхдлинные волны (СДВ): λ ≥10000 м, |
f ≤ 3 104 Гц, |
||||
Длинные волны (ДВ): |
λ =10000 ÷1000 м, |
f = 3 104 −3 105 Гц, |
|||
Средние волны (СВ): |
λ =1000 ÷100 м, f = 3 105 ÷3 106 Гц, |
||||
Короткие волны (КВ): |
λ =100 ÷10 м, |
f = 3 106 ÷3 107 Гц, |
|||
Ультракороткие волны |
|
|
|
|
|
(УКВ): |
λ =10 ÷1 м, |
f = 3 107 ÷3 108 |
Гц , |
||
Дециметровые волны |
|
|
|
|
|
(ДМВ): |
λ =1÷0,1 м, |
f = 3 108 ÷3 109 |
Гц , |
||
Сантиметровые волны |
|
|
|
|
|
(СМВ): |
λ = 0,1÷0,01 м, |
f = 3 109 ÷3 1010 Гц, |
|||
Миллиметровые волны |
|
|
|
|
|
(ММВ): |
λ = 0,01÷0,001 м, |
f = 3 1010 ÷3 1011 Гц, |
|||
λ = 0,001−0,0001 м, f = 3 1011 ÷3 1012 Гц.
Характер распространения волн различных диапазонов различен как при распространении вокруг земной поверхности, так и при распространении под землей, в воде, тропосфере и ионосфере, а также и в космическом пространстве.
Как было показано в третьей части (глава XVI), в однородной, изотропной и неограниченной среде (в «свободном пространстве») электромаг-
нитные волны распространяются прямолинейно со скоростью υ =1 εa µa . В
εa µa . В
атмосфере |
можно |
приближенно |
считать, |
что |
εa ≈ ε0 , µa ≈ µ0 , υ = 3 108 |
м сек. Волны, распространяющиеся в свободном |
|||
пространстве, будем называть свободно распространяющимися. |
|
|||
235

Рис. 17.1.
Представим теперь, что распространение радиоволн происходит вблизи плоской границы раздела двух сред, например, в атмосфере вблизи земной поверхности, отражающий участок которой можно считать гладким и плоским. Тогда пути распространения волн от источника (0) к приемнику (А) могут быть двоякого рода (рис. 17.1):
прямой луч (1) и отраженный луч (2) складываются в точке приема (А). Очевидно, что интерференция волн, приходящих к приемнику по пути 1 и 2, приводит к ряду явлений, которые необходимо учитывать; это прежде всего изменение диаграммы направленности излучателя за счет отражающей поверхности и искажение сигнала за счет разного времени распространения волн по пути 1.2.
Очевидно, что если неровности земной поверхности значительно превосходят рабочую длину волны, предыдущая картина значительно усложня-
Рис. 17.2.
ется за счет увеличения числа отраженных лучей (рис. 17.2).
Земная поверхность на достаточно высоких частотах по своим свойствам соответствует полупроводящей среде; поле волны, распространяющейся непосредственно над земной поверхностью, частично проникает в землю, за счет чего соответственно искажается структура поля над земной поверхностью. Образуется специфическая по структуре поверхностная волна, следующая вдоль искривлений земной поверхности, т.е. не прямолинейно. К такому же эффекту приводит явление дифракции электромагнитных волн вокруг сферической земной поверхности на достаточно длинных волнах, когда высота шарового сегмента h (рис. 17.3) сравнима с длиной волны λ.
236
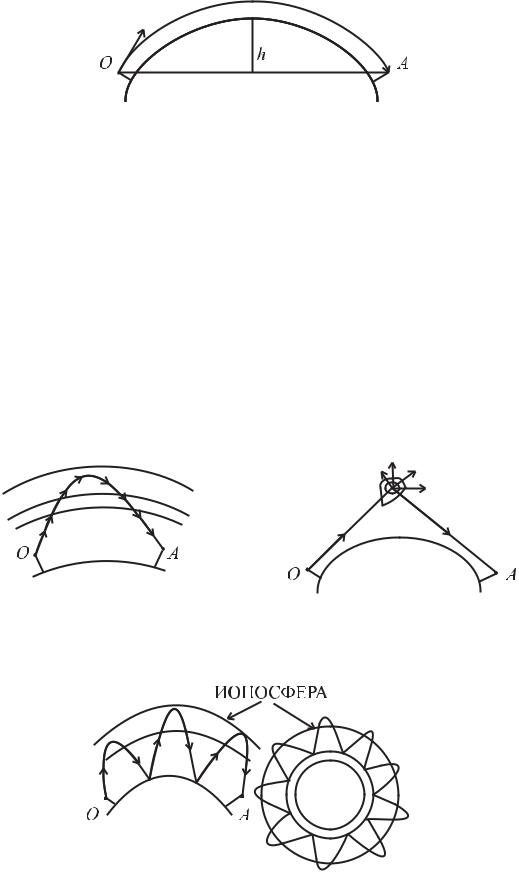
Рис. 17.3.
Следующие вдоль земной поверхности волны (независимо от механизма образования) принято называть общим термином – земные волны.
Над земной поверхностью расположена атмосфера, нижний (плотный) слой которой называется тропосферой. Тропосфера не является однородным диэлектриком – с увеличением высоты (расстояния от поверхности земли) плотность тропосферы падает, соответственно и ε несколько уменьшается; кроме того, в тропосфере всегда существуют нестационарные локальные неоднородности различного происхождения (облака, турбулентные слои и т.д.). За счет регулярной неоднородности тропосферы происходит искривление радиолуча (рис. 17.4), за счет случайных локальных неоднородностей (рис. 17.5) происходит рассеяние радиоволн. Как волноводное (направляющее радиолуч вдоль земной поверхности) действие тропосферы, так и рассеяние на неоднородностях приводит к дальнему распространению волн (до 1000 км). Волны, распространяющиеся таким образом, называются тропосферными.
Рис. 17.4. Рис. 17.5.
Над тропосферой на высотах 60 ÷600 км располагается ионосфера, представляющая собой слои частично или полностью ионизированного газа
Рис. 17.6
различной плотности и с различной электронной концентрацией. Волны с длиной волны λ>10 м отражаются от ионосферы и поэтому за счет последо-
237
вательных отражений радиоволн от ионосферы и земной поверхности возможно дальнее распространение в естественном волноводе ионосфера-земная поверхность (рис. 17.6)
Волны, имеющие описанный выше характер распространения, называ-
ются пространственными или ионосферными.
Радиоволны различных диапазонов распространяются в виде волн различного типа. Преимущество какого-либо вида распространения зависит от расстояния, времени суток, характера радиотрассы, метеорологических условий и т.д. Учет всех этих условий весьма сложен, и точный расчет радиотрассы почти всегда исключен; необходимы специальные тесты для выявления наилучшего диапазона и наилучшей радиотрассы при обеспечении связи между заданными географическими пунктами в заданное время года и суток.
238
ГЛАВА XVIII
ДИФРАКЦИЯ РАДИОВОЛН
18.1 Принцип Гюйгенса. Формула Кирхгофа
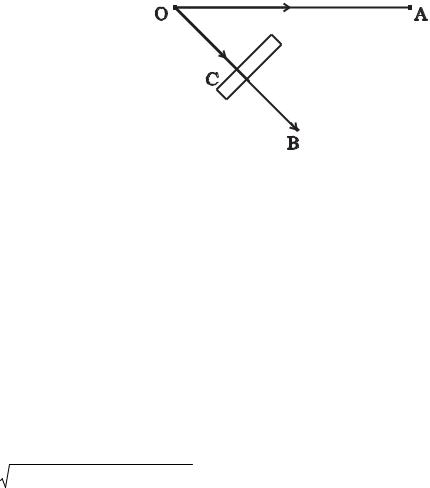
На распространение радиоволн от источника к приемнику существенное влияние, очевидно, оказывают свойства не всего окружающего пространства, а только некоторой его ограниченной области, расположенной между приемником и источником. Рис. 18.1 иллюстрирует этот очевидный факт – препятствие С (например, непрозрачный экран) существенно влияет на распространение волн к приемнику В, но, очевидно, мало влияет на интенсивность поля в точке приема А.
Для выяснения формы и размеров существенной области воспользуемся принципом Гюйгенса. Принцип Гюйгенса в простейшем понимании утверждает: каждая точка, лежащая на поверхности фронта распространяющейся волны, возбужденной первичным источником, является источником вторичных сферических волн. Новое положение фронта распространяющейся волны в пространстве есть огибающая суперпозиции вторичных сферических волн.
Рис. 18.1
Нетрудно заметить, что принцип Гюйгенса представляет собой частный случай использования фиктивных источников электромагнитного поля, которые вводятся для упрощения решения задач электродинамики (см. главу XV части 4). Поэтому далее можно было бы непосредственно использовать полученные в главе XV части 4 формулы для математической формулировки этого принципа. Представляется, однако, более оправданным использовать исторически сложившуюся математическую формулировку принципа Гюйгенса в виде формулы Кирхгофа.
Рассмотрим исходную структуру задачи, представленную на рис. 18.2. Пусть источник электромагнитных волн расположен в точке О, точка наблюдения – А(x, y, z), B(x’, y’, z’) – вспомогательная точка, r – расстояние
между А и В:
r = (x − x')2 + (y − y')2 −(z − z')2 .
239

Рис. 18.2
Замкнутая поверхность S изолирует объем V от источника, расположенного в точке О. Вторая замкнутая поверхность S’ ограничивает объем V, делая его конечным. Будем считать, что источником является элементарный электрический излучатель и его поле описывается электрическим потенциалом Герца Πe . В объеме V источника нет, Πe удовлетворяет однородному уравнению Гельмгольца:
r |
Πe = 0 |
, |
(18.1) |
2Πe + k 2 |
k 2 = ω2εаµа , εа , µа - действительные.
Введем также вспомогательную функцию ϕ , удовлетворяющую уравнению:
2ϕ + k2ϕ = −4πδ[(x − x ')(y − y ')(z − z ')] = −4πδ (A − B) (δ −дельта−функция) (18.2)
и имеющую вид ϕ = |
e− jkr |
. |
|
|
|
|
|
||
|
r |
|
|
|
Умножим уравнение (18.1) на ϕ , уравнение (18.2) – на – Πe и сложим. |
||||
В результате имеем: |
|
|
||
ϕ 2Πe − Πe 2 ϕ = 4πδ(А− В)Πe |
(18.3) |
|||
Проинтегрируем (18.3) по V и воспользуемся свойством δ -функции. |
||||
При этом получим: |
|
|
||
r |
|
(18.4) |
||
∫(ϕ 2Πe − Πe 2ϕ)dV |
= 4πΠe (A) |
|||
V
Используя для преобразования левой части вторую теорему Грина, находим:
|
|
r |
r e ∂ϕ |
r e |
|
|
|
|
∂Πe |
(A) |
(18.5) |
||||
|
ϕ |
r |
− Π |
|
|
||
∫ |
r dS = 4πΠ |
||||||
S+S' |
|
∂n |
|
∂n |
|
|
|
240

Устремляя S′ в (18.5) в бесконечность и помещая точку В на поверхность S, имеем:
r e |
|
1 |
r e ∂ϕ |
r |
|
|
||
|
∂Πe |
(18.6) |
||||||
Π |
(А) = − |
|
|
Π |
r − ϕ |
r |
|
|
4π |
∫ |
dS |
||||||
|
|
S |
|
∂n |
∂n |
|
|
|
Соотношение (18.6), выражающее поле Πe в точке наблюдения А через Πe в точках В поверхности S и вспомогательную, пока не доопределенную функцию ϕ , называется формулой Кирхгофа. Функция ϕ обычно называется функцией Грина. Теперь геометрия задачи принимает вид, указанный на рис. 18.3. Здесь дополнительно указано ρ- расстояние от источника до точки В на поверхности S.
Рис. 18.3
Выберем поверхность S специальным образом, как это показано на рис. 18.4. Тогда S=Sc+S0, где Sc – полусфера с радиусом rc, S0 – замыкающая ее
Рис. 18.4
плоскость, нормальная к лучу ОА.
Будем далее считать, что электромагнитное поле создается элементарным (точечным) электрическим излучателем, и поэтому (см. главу XIII):
r |
. cm r |
|
e− jk ρ |
r e− jk ρ |
|
|
||||||
I |
l |
|
|
|
||||||||
Πe (S) = |
|
|
|
|
|
|
= C |
|
, |
(18.7) |
||
j4πεaω |
ρ |
ρ |
||||||||||
|
|
|
|
|
|
|||||||
где Cr = |
|
. cm r |
|
|
|
|
|
|
||||
|
I |
l |
. |
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
||||
|
|
j4πε ω |
|
|
|
|
|
|
||||
|
|
|
a |
|
|
|
|
|
|
|||
241
Запишем теперь формулу Кирхгофа для рассматриваемого случая:
r e |
|
1 |
|
r e ∂ϕ |
|
r |
|
1 |
r e ∂ϕ |
||
|
|
|
∂Πe |
||||||||
Π |
(A) = − |
|
∫ |
Π |
r |
− ϕ |
r |
dS − |
|
∫ Π |
r |
|
|
||||||||||
|
|
4π S0 |
|
∂n |
|
∂n |
|
4πSC |
∂n |
||
r
− ϕ ∂Πe dS (18.8)
∂nr
Рассмотрим предел второго интеграла при rC → ∞, имея в виду, что Πe (S) оп-
ределяется (18.7). При таком переходе ввиду конечности расстояния ОА имеют место следующие пределы:
|
r |
→1; |
r |
, |
ρ |
→1, |
(18.9) |
|
ρ |
|
r |
||||
|
|
r |
|
|
|||
|
|
|
C |
C |
|
|
|
|
|
r |
|
|
|
|
(18.10) |
cos(n, lr )→ −1, |
|
||||||
|
|
r |
|
|
|
|
(18.11) |
cos(n, lρ )→ −1, |
|
||||||
В (18.10) и (18.11) |
r |
- единичные вектора вдоль направлений соот- |
|||||
lr , lρ |
|||||||
ветственно r иρ (от точек А и О).
Распишем последовательно элементы подынтегральных выражений, используя вид функции ϕ , (18.7), (18.9) ÷(18.11).
∂ϕ |
|
dϕ |
|
r r |
|
|
e−jkr |
|
|
1 |
|
|
r |
r |
|
|||||
r |
= |
|
|
|
cos(n, lr |
)= − jk |
|
1+ |
|
|
cos(n, lr ), |
|
||||||||
|
|
|
|
|
|
|
||||||||||||||
∂n |
|
dr |
|
|
|
|
|
r |
|
|
jkr |
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
r e |
|
|
|
r e |
r |
r |
r |
|
|
e |
−jkρ |
|
|
1 |
|
r |
r |
|||
∂Πr |
|
= |
dΠ |
cos(n, lρ )= C − jk |
|
|
1 |
+ |
|
cos(n, lρ ). |
||||||||||
|
|
|
|
|
|
|
||||||||||||||
∂n |
|
|
|
dρ |
|
|
|
|
|
|
ρ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
jkρ |
|
|
||||||
Таким образом, подынтегральное выражение имеет вид:
(18.12)
(18.13)
r |
|
|
|
|
e |
|
|
|
r |
−jkρ |
|
−jkr |
|
|
1 |
|
r r |
|||
Πe ∂ϕr |
− ϕ |
∂Πr |
= −jkC e |
|
|
e |
|
|
1 |
+ |
cos(n, lr )+ |
|||||||||
|
|
|
|
|
||||||||||||||||
∂n |
|
|
∂n |
|
|
|
|
ρ |
|
r |
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
jkr |
(18.14) |
|||||||||
r |
|
−jkr |
|
e |
−jkρ |
|
1 |
|
|
|
r |
r |
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|||||||||||
+ jkC |
e |
|
|
|
|
1 |
+ |
|
cos(n, lρ ) |
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
r |
|
|
ρ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
jkρ |
|
|
|
|
|
|
|
|
||||
Очевидно, что при |
|
rC → ∞ |
|
(r, ρ → ∞) |
и выполняются (18.9) ÷(18.11). |
|||||||||||||||
При этом (18.14) представляет собой разность одинаковых по величине чле-
нов. Учитывая, что Sc~r2 |
и ρ r → rc2 заключаем, что второй интеграл в (18.8) |
||||||||
при rc → ∞ обращается в нуль, и, следовательно, |
Πe (А) находится интегриро- |
||||||||
ванием по бесконечной плоскости S0, разделяющей О и А. Таким образом, |
|||||||||
r e |
|
1 |
|
r e ∂ϕ |
|
r |
|
|
|
|
|
|
∂Πe |
|
|||||
Π |
(A) = − |
|
∫ |
Π |
r |
− ϕ |
r |
dS . |
(18.15) |
|
|||||||||
|
|
4π S0 |
|
∂n |
|
∂n |
|
|
|
|
|
|
|
|
|
|
|
|
242 |
Проведем теперь дальнейшие упрощения (18.15). Очевидно, что инте-
грал (18.15) упростится, если положить ∂∂ϕnr (S0 ) = 0 илиϕ(S0 ) = 0 . Примем второе
условие, т.е. положим |
|
||||
ϕ(S0 ) = 0 . |
|
|
(18.16) |
||
Имея в виду, что общий вид ϕ указан выше, представим ϕ с учетом |
|||||
(18.16) следующим образом: |
|
||||
ϕ = |
e−jkr1 |
− |
e− jkr2 |
, |
(18.17) |
|
|
||||
|
r |
r |
|
||
1 |
|
2 |
|
|
|
где r1 – расстояние от точки А до любой текущей точки В, r2 – расстояние от точки А’, являющейся зеркальным изображением А относительно S0, до той же точки В (рис. 18.5). Очевидно, что для всех В S r1=r2 и ϕ=0, т.е. условие
A’ |
S0 |
A |
r2 r1 B
Рис. 18.5
(18.16) удовлетворяется.
Теперь
Рассчитаем
r e |
|
1 |
|
r e ∂ϕ |
||
Π |
(A) = − |
|
∫ |
Π |
r dS . |
|
4π |
||||||
|
|
S0 |
|
∂n |
||
|
|
|
|
|
||
∂∂ϕnr (S0 ) . Поскольку на
(18.18)
S0 r1=r2=r, выполняется также следующее
равенство:
|
|
|
|
r |
r |
|
|
|
|
|
r |
) , |
|
|
|
|
|
|
|
|
|
|
|||
−cos(n, lr1 |
) |
= cos(n, lr2 |
|
|
|
|
|
|
|
|
|
|
|||||||||||||
∂ϕ |
|
|
|
|
|
|
d |
|
e−jkr1 |
|
r r |
|
d |
e− jkr |
|
|
r |
r |
|
||||||
|
|
|
|
|
|
|
|
|
|||||||||||||||||
r |
|
|
|
= |
|
|
|
|
|
|
|
|
cos(n, lr |
)− |
|
|
|
|
cos(n, lr |
)= |
|||||
|
|
|
dr |
|
|
|
r |
dr |
r |
|
|||||||||||||||
∂n |
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
2 |
|
|||||
|
|
S0 |
|
1 |
|
|
|
1 |
|
|
|
2 |
|
d |
|
|
−jkr |
|
r r |
||||||
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
= (r1 |
= r2 = r, учитываем (18.19))= 2 |
e |
|
|
|
|
|||||||||||||||||||
|
|
|
|
||||||||||||||||||||||
|
|
|
r |
cos(n, lr )= |
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
dr |
|
|
|
|
||
|
|
|
|
∂ |
|
|
−jkr |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
= 2 |
|
|
|
e |
|
|
|
|
|
. |
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
r |
|
r |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
∂n |
|
|
|
|
|
S0 |
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(18.19)
(18.20)
243
