Содержание

Задание: 3

Часть 1 Задание:

1. Рассчитать проводимость системы на единицу длины. Найти ток утечки.

2. Рассчитать и построить графики распределения напряженности электрического поля и потенциала в плоскости KF.

3. Рассчитать и построить вектор плотности тока в точке М.

4. Провести эквипотенциаль с потенциалом, равным 0,25U, где U – приложенное напряжение.

Исходные данные:

Рисунок 8

R = 4 мм = 0.004 м;

d = 40 мм = 0.04 м;

h = 50 мм = 0.05 м;

U = 200 В;

σ = 4*10^-4 См/м

Рисунок 1.1. Схема задания

Решение:

1.1. Расчёт проводимости системы на единицу длины и тока утечки

Задача о поле двухпроводной линии сводится к задаче о поле двух заряженных осей. Расчет задачи проводим при помощи метода зеркальных изображений. Его суть заключается в следующем. В результате электростатической индукции на проводящей поверхности выступают заряды. Для расчета такой системы кроме заданных заряженных осей вводят ещё дополнительную фиктивную пару осей, линейные плотности зарядов которых будут равными по значению, но противоположные по знаку зарядам в реальной паре.

ε

Рисунок 1.2. Симметричная пара с радиусом жилы R₁ , расположеная в среде с проводимостью , и её зеркальное отображение.

Потенциал поля в любой точке:

где τ - линейная плотность заряда, Кл/м.

:

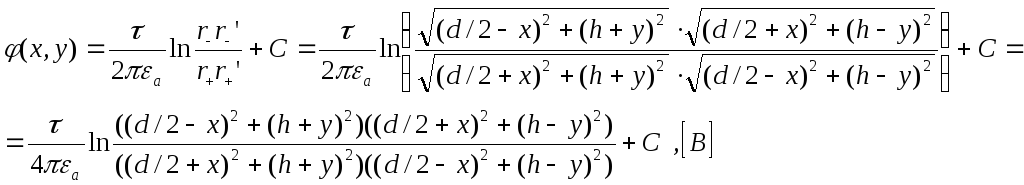
Константу С находим из условия: х=0, y=0, φ=0 (оси - эквипотенциальные поверхности с нулевым потенциалом):

Емкость системы на единицу длины:

Между параметрами стационарного электрического поля и электростатического поля существует аналогия:

Проводимость системы на единицу длины:

Ток утечки:

1.2. Рассчёт напряженности электрического поля и потенциала в плоскости kf

Потенциал в любой точке определяется по формуле:

Так как , то для нахожденияипродифференцируем выражениепоx и y, получим:

Подставим числовые значения. В плоскости KF потенциал и напряженность электромагнитного поля будут зависеть только от x, т. к. y=const= -0,05 м:

При построении графика зависимости Eотxбудем учитывать только х-овую составляющую.

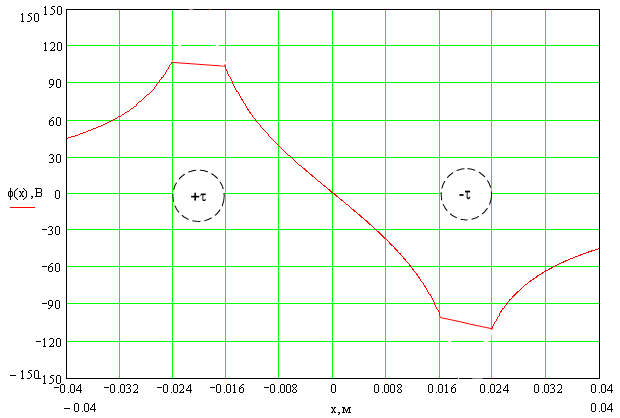
Рисунок 1.3. График распределения потенциала в плоскости KF.

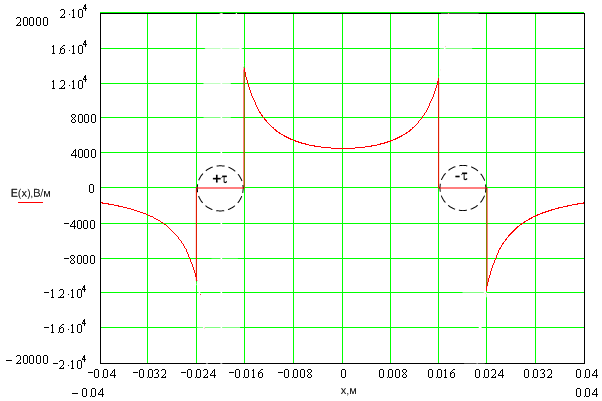
Рисунок. 1.4. График распределения напряженности электрического поля в плоскости KF.

1.3. Расчёт вектора плотности тока в точке м

Вектор плотности тока, электрической индукции, напряженности в однородной изотропной среде связаны между собой:

;

Отсюда видно, что ,исонаправлены.

Точка М имеет координаты x = -0.02; y = 0. Напряженность поля в точке М:

Модуль напряженности поля в точке М:

E=E_y=.

Вектор плотности тока:

Модуль вектора плотности тока:

j =

Рисунок 1.5. Вектор плотности тока.

1.4. Построение эквипотенциали с потенциалом, равным 0,25u

Потенциал в любой точке:

График, являющийся решением этого уравнения приведен на рисунке.1.6

Рисунок 1.6. Чертеж эквипотенциали.

1.6. Вывод

• Наибольшее значение Е(х) на поверхности проводников.

• При расчете и построении вектора плотности тока в точке М выяснили, что он имеет только y-составляющую.

• Эквипотенциаль определяется уравненим четвёртого порядка и представляет собой эллиптическую фигуру.