Здесь J&l - первая гармоника тока пучка, ESZ0 - усредненная по сечению
пучка Z - составляющая электрической напряженности волны S-го типа замедляющей системы.
ГЛАВА VIII
*НЕРЕГУЛЯРНЫЕ ВОЛНОВОДЫ
8.1.Неортогональные координатные системы
Пусть в заданной области V(S) введены обобщенные криволинейные координаты u1,u2,u3 , так, что любая точка P V определяется однозначно
набором значений u1,u2,u3 . В точке Р определены три координатные поверхности:
u1 = const, u2 = const, u3 = const . |
(8.1) |
Пересечение двух поверхностей образует координатную кривую, вдоль которой меняется только одна координата.
Положение точки Р определяется радиусом-вектором r , проведенным из начала отсчета. Как и точка Р, r является функцией криволинейных координат
u1,u2,u3 :
r |
r |
1 |
|
|
2 |
,u |
3 |
) . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(8.2) |
|||
r = r (u ,u |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
Приращение вектора r |
|
в соответствии с (2) определяется как |
|
||||||||||||||||||||||||
r |
|
|
|
|
∂r |
|
|
|
|
1 |
|
∂rr |
|
|
|
2 |
|
|
∂r |
|
3 |
|
|
||||
dr |
( p) = |
|
|
|
du |
|
+ |
|
|
|
du |
|
+ |
|
|
|
du |
|
. |
(8.3) |
|||||||
∂u1 |
|
∂u |
2 |
|
|
∂u3 |
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
Частные производные |
|
|
∂r |
|
представляют собой приращение r |
вдоль |
|||||||||||||||||||||
|
∂u1 |
|
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
касательных к координатным кривым в точке Р |
|
||||||||||||||||||||||||||
r |
|
|
∂rr |
|
|
r |
|
|
|
∂rr |
|
|
r |
|
|
|
∂rr |
|
|
|
|
||||||
a1 |
= |
|
, |
|
a2 |
= |
|
, |
|
|
a3 |
= |
|
. |
|
|
(8.4) |
||||||||||
∂u1 |
|
∂u2 |
|
|
∂u3 |
|
|
||||||||||||||||||||
Длина и размерность координатных векторов зависят от характера криволинейных координат u1, u2 , u3 . Смешанные произведения базисных векторов ar1, ar2 , ar3 дают объем V координатного параллелепипеда:
87
V = ar1[ar2,a3] = ar2[ar3,ar1] = a3[a1,a2].
Взаимную систему векторов a1,a2,a3 определим как |
|
|||||||||||||||||
r1 |
|
1 |
r r |
r |
2 1 |
|
|
r r |
|
r3 |
|
1 |
r r |
|
||||
a |
= |
|
|
[ a2 ,a |
3 ], a |
|
|
|
[ a3 ,a |
1], a |
|
= |
|
|
[ a1 ,a 2 ] . |
(8.5) |
||
V |
V |
|
|
V |
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
В соответствии с (8.5) ar1 перпендикулярен плоскости, определяемой |
||||||||||||||||||
парой (ar |
,ar |
), ar2 −(ar ,ar ), |
|
|
ar3 − (ar ar |
). Из определения (8.5) следует: |
|
|||||||||||
2 |
3 |
|
3 |
1 |
|
|
|
1 |
2 |
|
|
|
|
|
|
|||
r r |
=δij ,δij |
1,i = j |
|
. |
|
|
|
|
|
|
|
(8.6) |
||||||
aia j |
= |
|
|
j |
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
0,i ≠ |
|
|
|
|
|
|
|
|
|
||||
Основная система векторов выражается через взаимную аналогично
(8.5):
r |
|
1 |
r2 |
r3 |
|
r |
|
1 |
r3 |
r1 |
|
r |
|
1 |
r1 r2 |
|
|
||||
a |
= |
|
|
[a |
,a |
], |
a |
= |
|
|
[a |
,a |
], |
a |
= |
|
|
[a ,a |
]. |
(8.7) |
|
V |
V |
V |
|||||||||||||||||||
1 |
|
|
|
|
2 |
|
|
|
|
3 |
|
|
|
|
|||||||
Дифференциал drr во взаимной системе записывается через приращения du1, du2 , du 3 в направлении взаимных векторов:
r |
r1 |
r2 |
r3 |
du3 . |
(8.8) |
dr |
= a du1 |
+ a |
du2 + a |
Дифференциалы du1,du2,du3 могут быть не полными в неортогональных системах. Приравнивая (8.3) (с учетом (8.4)) и (8.8), имеем
drr |
3 |
3 |
|
|
= ∑aridui = ∑ar jdu j . |
|
(8.9) |
||
|
i=1 |
j=1 |
|
|
Используя (8.6) и умножая (8.9) скалярно на ari |
и затем на arj , получим |
|||
|
3 |
|
3 |
|
du j = ∑arjaridui ; dui = |
∑ariar jdu j . |
(8.10) |
||
|
i=1 |
|
j=1 |
|
Обозначим скалярные произведения основных и взаимных векторов, входя-
щие в (8.10):
gij = ari arj = g ji , g ij = ari ar j = g ji . |
(8.11) |
88
Тогда компоненты drr в основной и взаимной базисных системах будут связаны следующим образом:
3 |
dui = |
3 |
|
du j = ∑ g ji dui ; |
∑ g ij du j . |
(8.12) |
|
i=1 |
|
j=1 |
|
Любой вектор F , как и dr , может быть разложен на компоненты как в основной, так и во взаимной базисных системах:
r |
3 |
|
3 |
|
F |
= ∑ f iari = ∑ f jar j , |
(8.13) |
||
|
i=1 |
j=1 |
|
|
|
rr |
|
rr |
|
где f i = Fai , |
f j = Fa j . |
|
||
Последнее поясним: |
|
|||
r |
|
3 |
|
f i , |
Fari = |
∑ f jarjari = (с учетом (6))= |
|||
|
|
i=1 |
|
|
r |
|
3 |
|
|
Farj = |
∑ fiariarj = f j . |
(8.14) |
||
i=1
Аналогично (8.10) связи fj и f i выражаются в виде:
|
3 |
|
|
3 |
f j = ∑q ji f i , |
f i = ∑qij f j . |
|||
|
i=1 |
|
|
j=1 |
Итак, можно записать |
||||
r |
3 |
r |
3 |
r |
F |
= ∑(Fari )avi = ∑(Farj )ar j . |
|||
|
i=1 |
|
j=1 |
|
Проекции fi называются ковариантными компонентами вектора контравариантными.
Введем безразмерные единичные векторы Ii :
(8.15)
(8.16)
F, f i -
Ivi |
v |
|
ari . |
|
= vai v = |
1 |
(8.17) |
||
|
ai ai |
gij |
|
|
Тогда
89
|
Fr = F1Ir1 + F2Ir2 + F3Ir3 , |
(8.18) |
|||
где F |
= g |
ii |
f i |
- физические компоненты вектора F, |
имеющие ту же раз- |
i |
|
|
|
|
|
мерность, что и сам вектор F .
8.2. Дифференциальные операторы
Приведем без доказательства формулы основных дифференциальных операторов электродинамики.
Градиент скалярной функции ϕ(u1,u2 ,u3) в т. Р
3 |
∂ϕ |
|
|
|
gradϕ = ∑ari |
. |
(8.19) |
||
i |
||||
i=1 |
∂u |
|
||
Здесь градиент записан с использованием взаимной системы базисных векторов. Естественно, ari могут быть выражены через ai путем преобразования
r |
3 |
|
|
|
|
|
r |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(8.20) |
||
ai = |
∑ g ij ai . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
i=1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Дивергенция векторной функции F(u1,u2 ,u3) |
в точке Р |
|||||||||||||||||||||||||||
divFr = |
|
1 |
3 |
|
∂ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
∑ |
( f i |
|
g ) . |
|
|
|
|
|
|
|
|
|
|
(8.21) |
|||||||||||
|
|
|
g |
|
|
i |
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
i=1 |
∂u |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
Здесь f i – контравариантные проекции F, |
|
|
rr |
|
|
|
||||||||||||||||||||||
f i = Fai |
|
|
|
|||||||||||||||||||||||||
|
g11 g12 g13 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
g = g21 g22 g23 , g = ar1 [ ar2 ,ar3 ] =V . |
|
|
|
|
|
|
||||||||||||||||||||||
|
g31 g32 g33 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
Ротор вектора F, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
r |
|
|
|
|
|
|
|
|
|
∂f |
|
|
|
∂f |
|
|
∂f |
∂f |
|
|
|
∂f |
|
|
∂f |
|
||
|
|
|
1 |
|
|
|
3 |
|
|
2 |
r |
3 |
r |
|
2 |
|
r |
|||||||||||
rotF |
= |
|
|
|
|
|
|
{( |
|
|
− |
|
)a + ( |
1 |
− |
|
)a |
+ ( |
|
− |
1 |
)a } . (8.22) |
||||||
|
|
|
|
g |
|
|
|
|
∂u3 |
|
∂u1 |
∂u1 |
∂u2 |
|||||||||||||||
|
|
|
|
|
|
|
|
|
∂u2 |
1 |
∂u3 |
2 |
|
|
3 |
|||||||||||||
|
rr |
|
|
- ковариантные проекции F . |
|
|
|
|
|
|
||||||||||||||||||
Здесь fi = Fai |
|
|
|
|
|
|
|
|
||||||||||||||||||||
Оператор Лапласа от скалярной функции ϕ(u1,u2 ,u3)
90
|
1 |
3 |
3 |
∂ |
|
|
∂ϕ |
|
|
∆ϕ = divgradϕ = |
∑∑ |
(gij |
g |
). |
|||||
|
i |
j |
|||||||
|
g i=1 j=1 |
∂u |
|
∂u |
|||||
(8.23) |
|
|
|
|
|
|
|
|
|
8.3. Продольно-азимутально нерегулярный волновод. Контравариантные компоненты уравнений Максвелла
Рассмотрим произвольно нерегулярный прямолинейный волновод (продольно-азимутально нерегулярный волновод). Пусть внутренняя граница такого волновода задается следующей произвольной гладкой функцией:
b = b(ϕ, z) , |
(8.24) |
где ρ = r / b .
Тогда радиус-вектор внутренней точки Р (8.2) может быть задан как
rr(ρ,ϕ, z) = zzr0 + ρb{xr0 cosϕ + yr0 sinϕ)
В соответствии с (8.4) тогда имеем ar1 = ∂rr = brr0 ,
∂ρ
r |
|
|
∂rr |
r |
|
|
r |
∂b |
|
a2 |
= |
|
|
=ϕ0 ρb |
+ r0 ρ |
|
, |
||
|
∂ϕ |
∂ϕ |
|||||||
r |
|
∂rr |
r |
r |
|
∂b |
|
|
|
a3 |
= |
|
∂z = z0 |
+ r0 |
ρ |
∂z . |
|
||
Соответственно V = ar1[ar2 ,ar3] = ar2[ar3
.
,ar1] = ar3[ar1,ar
ветствии с (8.5) система взаимных векторов имеет вид
ar1 = b12 (rr0b −ϕr0 ∂∂ϕb − zr0ρb ∂∂bz ) ,
ar2 =ϕr |
/bρ, |
ar3 = zr . |
0 |
|
0 |
(8.25)
(8.26)
2] = b2 ρ . Тогда в соот-
(8.27)
Запишем первое уравнение Максвелла, используя основную (8.26) и взаимную (8.27) системы векторов. При этом для сохранения привычных выражений для компонент rotH в цилиндрической системе координат введем
«расчетные» (со штрихом) компоненты векторов H = Hρ′ ar1 + ρHϕ′ar2 + Hz′ar3
91
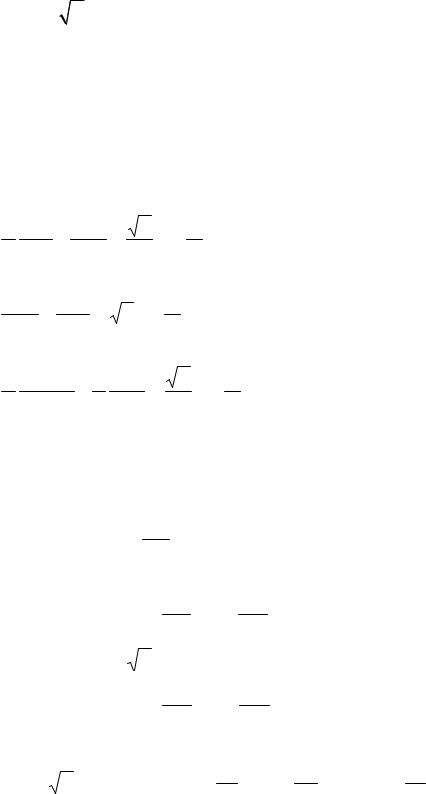
(т.е. |
ковариантные |
|
|
|
проекции |
векторов |
|
связаны |
|
|
с |
|
|
расчетными |
|||||||||||||||||||||||||||||||
|
|
|
|
|
rr |
|
|
′ |
|
|
|
′ |
= H1, |
|
|
|
′ |
= H |
3 ), |
|
|
′ |
r |
1 |
+ |
|
|
′ |
r |
2 |
|
′ |
r |
3 |
и т.д.. |
||||||||||
какH2 = Ha2 = ρHϕ , H ρ |
|
H z |
E = Eρa |
|
|
ρEϕa |
|
+ Ez a |
|
|
|||||||||||||||||||||||||||||||||||
Тогда |
|
|
|
1 ∂H′ |
|
|
∂Hϕ′ |
|
|
|
|
|
|
|
∂Hρ′ |
|
|
∂H′ |
|
|
|
|
|
|
|
1 ∂(ρHϕ′) |
|
|
|
|
∂Hρ′ |
|
|||||||||||||
|
|
r |
|
|
ρ |
|
|
|
|
|
r |
|
|
1 |
|
|
|
|
r |
|
|
|
|
|
|
1 |
|
r |
|||||||||||||||||
rotH = |
|
|
{( |
|
|
z |
− |
|
|
|
|
|
)a |
+ |
|
|
( |
|
|
− |
z |
)a |
+ |
( |
|
|
|
|
|
|
|
|
− |
|
|
|
|
)a } = |
|||||||
|
g |
|
|
|
∂z |
|
|
ρ |
∂z |
|
|
ρ |
|
|
∂ρ |
|
ρ |
∂ϕ |
|||||||||||||||||||||||||||
|
|
|
|
|
|
|
ρ ∂ϕ |
|
|
|
1 |
|
|
|
|
|
|
∂ρ |
|
2 |
|
|
|
|
|
|
|
|
|
3 |
|||||||||||||||
|
|
|
∂Eρ′ |
r |
|
∂(ρEϕ′ ) r |
|
|
|
∂E′ |
r |
|
|
|
|
r |
|
|
r |
|
|
|
|
|
r |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
=ε |
|
{ |
|
|
a1 + |
|
|
|
a |
2 |
+ |
|
|
z |
a |
3} +δ′a1 |
+ ρδ′a |
2 |
+ |
δ′a |
3 . |
|
|
|
|
|
|
|
|
|
(8.28) |
||||||||||||||
|
∂t |
|
|
∂t |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||
|
a |
|
|
|
|
|
|
|
|
|
|
∂t |
|
|
|
|
|
ρ |
|
|
ϕ |
|
|
z |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
Умножая обе части (8.28) скалярно последовательно на взаимные векторы ar1,ar2 ,ar3 , получаем контравариантные проекции уравнений Максвелла в следующей форме:
1 ∂H ′ |
∂Hϕ′ |
|
g |
|
∂ |
|
|
11 |
′ |
|
|
|
|
12 |
|
|
′ |
|
|
13 |
′ |
|
11 |
|
′ |
|
|
12 |
|
′ |
|
|
13 |
′ |
|
||
|
z |
− ∂z = ρ |
{ εa ∂t ( g |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
ρ ∂ϕ |
|
Eρ |
+ g |
|
ρEϕ + g |
|
Ez |
) + g δ |
ρ + g |
|
ρδϕ + g |
|
δ z |
} |
|||||||||||||||||||||||
∂H ′ |
|
′ |
|
|
|
∂ |
|
21 |
|
|
|
|
22 |
|
|
|
|
|
23 |
|
|
|
|
21 |
|
|
22 |
|
|
|
|
23 |
|
|
|
|
|
ρ |
− |
∂H z |
= |
g{ ε |
( g |
E′ |
+ g |
ρE′ |
+ g |
E′ |
|
|
+ g |
ρδ ′ |
+ g |
δ ′ |
}, |
|
|||||||||||||||||||
∂z |
∂ρ |
a ∂t |
|
|
|
|
) + g δ ′ |
|
|
|
|||||||||||||||||||||||||||
|
|
|
|
|
|
|
ρ |
|
|
|
|
|
|
ϕ |
|
|
|
|
z |
|
|
ρ |
|
|
|
|
|
ϕ |
|
|
|
z |
|
|
|||
1 ∂( ρHϕ′ 1 ∂Hϕ′ |
|
|
g |
|
|
∂ |
|
31 |
|
|
′ |
|
|
32 |
|
|
′ |
|
33 |
′ |
|
|
|
|
|
|
|
|
|
|
|
|
|||||
ρ ∂ρ − ρ ∂ϕ = ρ { εa ∂t ( g |
E |
+ g |
|
|
+ g |
+ |
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
|
ρ |
|
ρEϕ |
|
Ez ) |
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
+ g 31δ ρ′ + g 32 ρδϕ′ |
+ g 33δ z′ } . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(8.29) |
|
||||||||||
В векторной форме уравнение (8.29) можно теперь записать в виде
r
rotHr′ = εa g) ∂∂Et ′ + g)δr′, (8.30)
g11ρ
где g) = g g 21
g 31ρ
g12 |
g13 |
|
|
|
ρ |
|
|
||
|
|
|
||
ρg 22 |
g 23 |
|
, |
|
|
||||
g 32 |
g |
33 |
|
|
|
|
|
||
|
ρ |
|
|
|
|
|
|
|
|
g =V = b |
2 |
ρ, g |
11 |
= |
1 |
( b |
2 |
+( |
∂b |
) |
2 |
+ ρ |
2 |
b |
2 |
( |
∂b |
) |
2 |
), |
|
|
b4 |
|
∂ϕ |
|
|
|
∂z |
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
92