18.3. Дифракция электромагнитных волн от края непрозрачного экрана

.

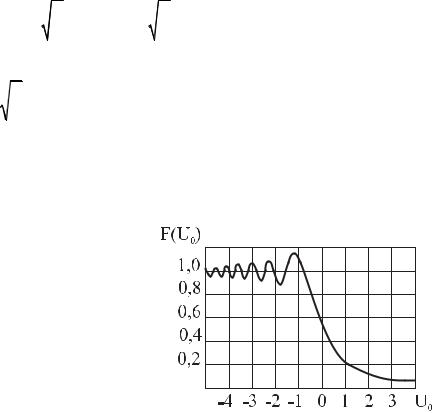
График модуля | F(u0 ) | = F(u0) приведен на рис. 18.12.

Рис. 18.12

Из анализа приведенного графика следует: 1) в области тени (u0>0) поле не исчезает, за счет явления дифракции поле остается конечным при достаточно больших u0; 2) в открытой области F(u0) имеет осциллирующий характер, причем при u0 ≈ −1,2 F(u0) достигает максимального значения (Fmax =

1,175), т.е. Πe (A) имеет большее значение, чем если бы экрана не было.

Тот и другой вывод хорошо объясняются с точки зрения зон Френеля: в тени часть зон Френеля оказывается не закрытой экраном и за счет вторичных источников в этой не закрытой части существенной области возбуждается поле в точке А; при u0 ~ -1,2 экран перекрывает зоны таким образом, что «отрицательные» зоны закрыты больше, чем положительные, поэтому результирующее поле в точке А оказывается усиленным. Если бы речь шла о дифракции на круглом отверстии в непрозрачном экране, то при выборе его диаметра равным диаметру первой зоны Френеля, можно было бы перекрыть все высшие зоны, и тогда, как мы знаем, Πe (A)= Π1e =2 Πe ( Πe - поле в открытом пространстве), т.е. F=2.

В заключение заметим, что метод Кирхгофа дает заниженные значения для Πe (A) в области тени. Это связано с пренебрежением искажениями поля на крае препятствия и, особенно, с пренебрежением влияния токов, затекаю-

250

щих на теневую сторону препятствия (особенно, в случае проводящих препятствий). Ошибка может достигать многих порядков.

К настоящему времени предложены более совершенные приближенные методы учета дифракционных полей, из которых следует упомянуть метод дифракционных лучей, в котором учитываются «ползущие» вокруг поверхности препятствия волны, связанные с затеканием токов на теневую сторону (П.Я. Уфимцев «Метод краевых волн в физической теории дифракции». М., Сов. Радио, 1962 г.), а также более сильный метод параболического уравнения, в котором учитывается поперечная диффузия дифракционных лучей (В.А. Фок, Дифракция радиоволн вокруг земной поверхности. АН СССР, 1946 г.).

251

ГЛАВА XIX

ОТРАЖЕНИЕ И ПРЕЛОМЛЕНИЕ ВОЛН НА ГРАНИЦЕ РАЗДЕЛА ДВУХ СРЕД

19.1. Отражение и прохождение волн при нормальном падении на плоскую границу раздела

Пусть плоская электромагнитная волна, проходящая в среде 1 падает нормально на плоскую границу, разделяющую среду 1 и среду 2 (рис. 19.1). Среда 1 характеризуется параметрами ε1 , µ1 , среда 2 - ε2 , µ2 (значок «а» у εа иµа здесь и далее опустим для сокращения записи). Непосредственно на

границе раздела существуют три вида волн: падающая (Е0 , Н0 ), отраженная (Е− , Н− ), проходящая (Е+ , Н+ ). Мы будем предполагать, что как среда 1, так и среда 2 однородны и изотропны, поэтому волны в обеих средах распространяются прямолинейно и нормально к границе, как это изображено на рис. 19.1.

Е, Н, заданной на рис. 19.1 (действительная относительная ориентация, т.е.

252

Запишем уравнение связи между компонентными амплитудами трех волн на границе раздела двух сред (z = 0). Предположим, что на границе раздела поверхностных токов нет; тогда тангенциальные составляющие как Е, так и Н полного (суммарного) поля при переходе границы должны быть непрерывными (см. главу II первой части). В рассматриваемом случае все компоненты Е и Н являются тангенциальными, и поэтому

Введем для удобства дальнейших расчетов коэффициент отражения и коэффициент прохождения

Таким образом, амплитуды отраженной и проходящей волн могут быть выражены как

253

де с большой оптической плотностью (например, в диэлектрике с очень большим ε ), а среда 2 имеет относительно большое волновое сопротивление. В этом случае получаем, что ρ=1, а τ = 2 . Последнее, однако, не говорит о

254