Сущность его поясняется на рис. 20.20. Фазовая скорость υΦ1 распростране-

.

Рис. 20.20

ния поверхностных волн над морем больше, чем скорость υΦ2 распространения этих волн над сушей. Вследствие этого точка, лежащая на фронте волны А, проходит над сушей путь АА’ – меньший, чем путь ВВ’, проходимый точкой В над морем. В результате фронт волны над сушей оказывается развернутым на угол α; на тот же угол изменяется направление распространения волн. Поэтому из точки наблюдения a источник виден в направлении на точку 0' , а не на точку 0, где он действительно расположен. Угол α называется углом рефракционной ошибки; при отладке работы береговой радиолокационной станции он тщательно измеряется и учитывается на каждом из рабочих диапазонов.

20.9. Дифракция радиоволн вокруг сферической земной поверхности

В диапазоне длинных и сверхдлинных радиоволн существенное значение имеет дифракция радиоволн вокруг сферической земной поверхности. Если приемная и передающая антенны закрыты шаровым сегментом высоты h и h меньше радиуса существенной области R n , в точке приема А будет существовать достаточно заметное дифракционное поле (рис.20.21). Поскольку R n ~ λ , чем больше λ, тем существеннее явление дифракции и, наоборот, с уменьшением λ явление дифракции становится все более несущественным

Рис. 20.21

287

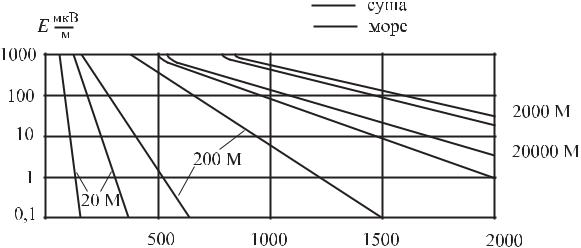
при расчете поля в точке приема. На рис 20.22 представлены зависимости напряженности дифракционного поля в точке приема в зависимости от рас-

288

ГЛАВА XXI

РАСПРОСТРАНЕНИЕ РАДИОВОЛН В ТРОПОСФЕРЕ

21.1 Строение тропосферы

Тропосферой называется нижняя часть атмосферы до высоты порядка 15 км. Если предположить, что состав газов и температура не меняются по высоте, то давление в атмосфере определяется известной барометрической формулой

где h – высота, R=8,32 Дж/град.моль, T – абсолютная температура, g – ускорение силы тяжести, M – масса грам-молекулы газа.

На самом деле температура в тропосфере не остается постоянной, а падает с высотой приблизительно на 50 С с каждым километром, поэтому формула (21.1) имеет приближенный характер. Состав же тропосферы действительно остается постоянным по высоте и составляет: 78% - молекулярный азот, 21% - молекулярный кислород, 1% - прочие составляющие – озон, пары воды, углекислый газ и др.

Относительная диэлектрическая проницаемость тропосферы определяется следующей эмпирической формулой:

Здесь Рп – парциальное давление паров воды в тропосфере. Как видно из (21.2), водяные пары существенно изменяют значение ε тропосферы, что связано с большим значением ε для воды. Ввиду малого отличия ε от 1 показатель преломления тропосферы можно записать в виде

Для удобства действия с числовыми величинами, характеризующими n тропосферы, обычно используется величина N, называемая индексом преломления

N = (n −1)106

289

Индекс преломления тропосферы сильно зависит от высоты, метеорологических условий, времени года и широты. На высоте 9 км N=109 и не меняется в зависимости от времени года и широты.

21.2. Поглощение радиоволн в тропосфере

Поглощение радиоволн в тропосфере существенно только в дециметровом и более коротковолновых диапазонах. Это поглощение обусловлено, в основном, тремя факторами.

1)Поляризационные потери на каплях воды.

2)Рассеяние радиоволн на неоднородностях (каплях воды, микротурбулентностях, пылевых включениях и т.п.).

3) Резонансное поглощение на частотах энергетических переходов молекул Н2О (нескомпенсированный электрический момент) и молекул О2 (нескомпенсированный магнитный момент). Резонансное поглощение является селективным и существенно в узком диапазоне длин волн.

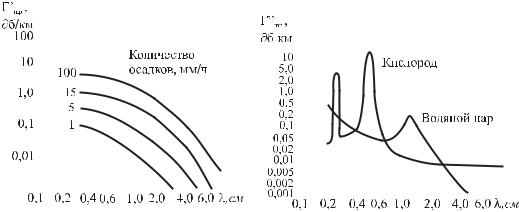
Суммарные потери в тропосфере характеризуются коэффициентом по-

глощения αТ (Hn / км) :

E(rr) = E0 (rr)e−αT r = E0 (rr) 10−0.05ГТr

где Е0 – напряженность поля волны без влияния потерь, Е – действительная напряженность поля.

В расчетах обычно используется значение коэффициента затухания в дБ/км (Гт).

.

290