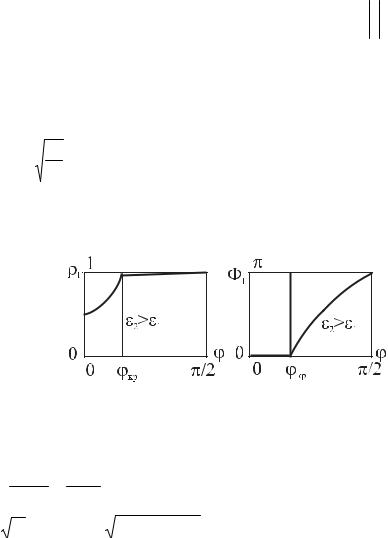
Очевидно, что существует ϕ = ϕкр , при котором ρ. впервые становится

При ϕ > ϕкр выражение для ρ. г ввиду того, что вторые члены в числите-

Рис. 19.5

ле и знаменателе оказываются мнимыми, принимает вид:

Графики ρг , Φг имеют вид, изображенный на рис. 19.5.

19.3. Наклонное падение вертикально-поляризованной волны на плоскую границу раздела двух сред

260

Введем коэффициенты отражения и прохождения. Для их определения

.

теперь удобно воспользоваться Нτ , поскольку вектор Н параллелен границе раздела и Hr. = xr0 H. x . Положим

Проанализируем функцию ρ. B (ϕ) в простейшем случае, когда обе среды являются идеальными диэлектриками, т.е. ε1'',2 = 0, µ1'',2 = 0, µ1 = µ2 = µ0 . В этом случае

262

Пусть ε2 > ε1 , т.е. отражения происходят от оптически более плотной среды. Представим, как и ранее,

ϕ → 900 , cosϕ → 0, sin ϕ →1, ρ. = −1, ρ =1, ΦB =1800.

Отсюда следует, что должен существовать такой угол ϕ0 , при котором

ρ. = 0; угол ϕ0 называется углом Брюстера. Из (19.37) находим

Напомним, что в случае горизонтальной поляризации углов ϕ0 , при ко-

торых ρ. = 0 не существует, т.е. описанное явление характерно только для вертикально поляризованных волн. Физическая сущность этого явления состоит в следующем. Из второго закона Снеллиуса (19.18) находим

sin ϑ0 = εε1 sin ϕ0 = cosϕ0 .

2

Таким образом, допустимое направление распространения отраженной волны z2 и направление распространения преломленной волны z3 ортогональны (рис. 19.7), т.е. yr03 || zr02 .

263

Рис. 19.7

Вектор же Еr + ориентирован по yr03 . В таком же направлении колеблют-

ся электрические заряды в среде 2. Эти колеблющиеся заряды представляют собой элементарные электрические диполи, ориентированные по yr03 . Отра-

женная волна образуется за счет их суммарного излучения. Однако диаграмма направленности элементарного электрического диполя такова (см. главу 13 из части 4), что вдоль оси диполя (в нашем случае yr03 ) излучение отсутст-

вует. Поэтому, если yr03 || zr02 , отраженная волна не возникает. В случае же горизонтальной поляризации Er || xr0 отраженная волна всегда существует. Если

на границу раздела диэлектриков падает электромагнитная волна с произвольной поляризацией при ϕ = ϕ0 , то отраженная волна будет иметь линей-

ную – горизонтальную поляризацию.

Построим теперь ход зависимостей ρВ (ϕ) и ΦВ (ϕ) (рис. 19.8)

Рис. 19.8

Пусть теперь ε1 > ε2 . Тогда зависимости ρВ (ϕ) и ΦВ (ϕ) изменяются за счет того, что будет существовать ϕ = ϕкр , начиная с которого ρВ =1. Как и в предыдущем случае (горизонтальная поляризация) ϕкр определяется условием

264