ГЛАВА II
ГРАНИЧНЫЕ УСЛОВИЯ ДЛЯ ВЕКТОРОВ ЭМП
Во многих задачах электродинамики вводятся границы раздела двух сред, обладающих различными электрическими и магнитными свойствами, т.е. εa , µa , σ для двух сред различны (достаточно, конечно, различия и одно-
го из параметров).
В связи с тем, что свойства среды меняются скачкообразно в макроскопическом приближении, вектора ЭМП терпят разрыв на границе раздела двух сред. Это означает, что дифференциальные соотношения на границе теряют смысл. Поэтому здесь в дополнение к УМ вводятся граничные условия (ГУ), связывающие тангенциальные (касательные) и нормальные составляющие векторов поля на обеих сторонах границы.
Эти ГУ устанавливаются с помощью уравнений Максвелла в интегральной форме.
2.1. ГУ для тангенциальных составляющих векторов ЭМП
Граничные условия для тангециальных составляющих электрического поля
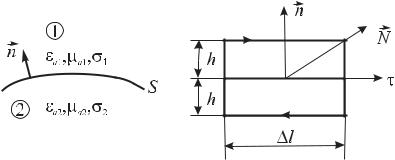
Рассмотрим границу раздела двух сред (рис. 2.1.)
Рис. 2.1. Рис. 2.2.
Выделим элементарный плоский прямоугольный участок вблизи границы, отвечающий следующим трем условиям:
1)границу в его пределах можно считать плоской;
2)среды 1 и 2 в пределах этого участка однородны;
3)поля в пределах этого участка не изменяются.
Введем систему векторов, определяющих ориентацию плоскости участка и направление обхода его границы (рис. 2.2):
1) nr - вектор нормали к S, направление и антинаправление вертикальных перемещений по контуру участка;
15
2)τr - тангенциальный к S вектор, направление и антинаправление горизонтальныхr перемещений по контуру участка;
3)N - вектор бинормали, направление вектор-площади участка.
Три вектора образуют правую тройку: τr = [N, nr]. Запишем второе УМ в интегральной форме:
|
|
r |
|
r |
r |
∂B |
r |
∫Edl = −∫ |
∂t |
dSN. |
|
l |
s |
|
|
|
|
||
Применим его к выделенному элементарному участку, используя его свойства:
|
|
r |
r |
2 |
∂Bi |
r |
|
|
||
|
∆lτr(E1 |
− E2 )+ ∆hE = −∑ |
h∆lN, |
|
(2.1) |
|||||
|
|
|
||||||||
|
|
|
|
|
i =1 |
∂t |
|
|
||
|
∆hE - элемент циркуляции E по вертикальным участкам контура. |
|||||||||
|
Перейдем к пределу h → 0. Учтем при этом, что на границе |
|||||||||
r |
|
r |
|
|
|
|
|
|
||
|
∂B |
|
|
|
|
|
|
|
||
E |
→/ ∞, |
|
→/ ∞, и поэтому правая часть уравнения и ∆ |
hE |
обращаются в |
|||||
|
||||||||||
1,2 |
|
∂t |
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|||
нуль. В итоге получаем |
|
|
|
|
|
|||||
|
r |
r |
Е1τ − Е2τ = 0 , |
|
|
|||||
|
τr(E1 − E2 )= 0 или |
|
(2.2) |
|||||||
т.е. тангециальные составляющие E непрерывны при переходе границы раздела любых двух сред. Физически это связано с тем, что поверхностных магнитных токов не существуетr . Придадим общность полученному ре-
зультату. Учтем, что τr = [N, nr]. Тогда
r |
r |
|
r |
− E |
|
)]N = 0. |
(E |
− E |
2 |
)[N , nr ]= [nr,(E |
2 |
||
1 |
|
1 |
|
|
||
|
|
|
|
|
|
r |
Наши результаты справедливы для любой ориентации N площадки. |
||||||
|
|
|
r |
|
|
|
Ввиду произвольности N получаем: |
||||||
|
r |
− E2 )]s = 0. |
|
|
|
|
[nr, (E1 |
|
|
(2.3) |
|||
Граничные условия для тангециальных составляющих напряженности магнитного поля
Запишем первое УМ в интегральной форме:
16
r r r |
r |
r |
∫ Hd l = ∫δ |
dSN + ∫∂∂Dt |
dSN. |
ls s
Применим это уравнение к ранее рассмотренному элементарному участку, используя его три свойства:
r |
r |
r |
2 |
∂D |
|
r |
2 r |
r |
|
|
|
|
∆lτ |
(H1 |
− H2 )+ ∆hH = ∑ |
i |
h∆lN + ∑δi ∆lhN. |
|
|
(2.4) |
|||||
|
|
|
||||||||||
|
|
|
i =1 |
∂t |
|
|
i =1 |
|
|
|
|
|
|
|
|
|
|
|
|
r |
|
r |
|
||
Перейдем к пределу h → 0. |
|
|
|
∂Di |
|
|
||||||
При этом H1,2 |
→/ ∞, |
→/ |
∞ на S. |
|||||||||
|
||||||||||||
|
|
|
|
|
|
|
|
|
∂t |
|
||
Но для тока такое утверждение неверно, поскольку при определенной идеализации ток может протекать по поверхности, не занимая объем (поверхностный ток).
Такая ситуация возникает в случае, когда одна из сред предполагается идеально проводящей. Введем понятие поверхностного тока:
r |
|
r |
A |
|
|
|
δS |
= liт hδ |
|
|
. |
(2.5) |
|
|
||||||
|
h→0 |
|
M |
|
|
|
С учетом сказанного в пределе h → 0 получаем |
|
|||||
|
r |
|
|
|
r r |
|
τr(H1 − H 2 )= δS N , или H1τ − H 2τ = δSN , |
(2.6) |
|||||
т.е. разрыв тангенциальных составляющих H равен поверхностному |
||||||
электрическому току. |
|
|
||||
Проведем обобщение: |
|
|||||
r |
r |
|
r |
|
|
|
[N |
, nr](H1 |
− H 2 )= [nr, (H1 − H 2 )]N = δS N. |
|
|||
В связи с произвольной ориентацией N имеем |
|
|||||
|
r |
|
|
|
r |
|
[nr, (H1 − H 2 )]= δS . |
(2.7) |
|||||
Физически этот разрыв обусловлен возникновением двойного магнитного слоя на поверхности, где протекает поверхностный ток.
2.2. ГУ для нормальных составляющих векторов ЭМП
ГУ для нормальных составляющих векторов D
17
Рассмотрим цилиндрический |
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|||
объем ∆V с основанием ∆S и высотами h |
|
|
|
|
|
|
|
|
|
|
|
|
||
в 1 и 2 средах (Рис.2.3). |
|
|
|
|
|
|
|
|
|
|
|
|
||
Объем будем считать |
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|||
элементарным со следующими |
|
|
|
|
|
|
|
|
|
|
|
|
||
признаками: |
|
|
|
|
|
|
|
|
|
|
|
|
||
1) |
в пределах ∆V - ∆S – плоская; |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
2) |
в пределах ∆V среды 1 и 2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
однородные; |
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|||
3) |
в пределах ∆V поля в средах 1 и |
|
|
|
|
|
|
|
|
|
|
|
|
|
Рис. 2.3. |
||||||||||||||
2 не изменяются |
||||||||||||||
Запишем третье УМ в интегральной форме:
∫DdSnr r = q = ∫ ρ dV .
S |
∆V |
Поскольку существуют поверхностные заряды, введем понятие о плотности поверностного заряда:
|
|
|
|
K |
|
|
|
|
|
|
||
|
ρS = liтhρ |
|
|
|
|
. |
|
|
(2.8) |
|||
|
|
м |
2 |
|
|
|
||||||
|
|
h→0 |
|
|
|
|
|
|
|
|
||
|
Перепишем третье УМ, учитывая все признаки элементарности ∆V: |
|||||||||||
|
|
r |
r |
|
|
+ Фбоке |
2 |
|
|
|||
|
nr0 ∆S(D1 |
− D2 ) |
= ∑ρi ∆Sh, |
|
(2.9) |
|||||||
|
|
|
|
|
|
|
|
|
|
i=1 |
|
|
Фбоке - электрический поток через боковую поверхность цилиндра. |
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
r |
|
|
Перейдем теперь к пределу h → 0 |
, учитывая, что D1,2 |
→/ ∞ и поэтому |
|||||||||
Фе |
→ 0 . При этом получим |
|
|
|||||||||
бок |
nr |
r |
r |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
, |
|
|
(2.10) |
||||
|
(D − D )= ρ |
S |
|
|
||||||||
|
0 |
1 |
2 |
|
|
|
|
|
|
|
||
т.е. разрыв нормальных составляющих D равен поверхностной плотности электрического заряда на граничной поверхности.
Если ρS = 0, то D1п = D2n или εa1E1n нормальных составляющих вектора E :
E1n = εa2 .
E2n εa1
=εa2 E2n и имеет место разрыв
(2.11)
18
Аналогичные действия с третьим УМ приводят к следующему резуль-
тату для Hn : |
|
|
||
|
H1n |
= |
µa2 . |
(2.12) |
|
|
|||
|
H2n |
µa1 |
|
|
Важным частным случаем является тот, когда среда 2 идеализируется как бесконечно проводящая. В этом случае на любой частоте поле в эту среду не проникает. Тогда полученная система ГУ преобразуется в следующую:
r |
|
r |
r |
|
|
|
|
|
|
|
|
|
|
|
[nr, E] |
= 0, |
[nr, H ] |
=δ |
S |
, |
D |
= ρ |
S |
, H |
1n |
|
S |
= 0 . |
(2.13) |
|
||||||||||||||
S |
|
S |
|
|
1n |
|
|
|
|
|
||||
В этом случае достаточно двух условий:
Eτ |
|
S = 0, Нn |
|
S = 0 . |
(2.14) |
|
|
В заключение необходимо отметить, что ГУ, сформулированные выше, относятся к простейшему случаю: граница S гладкая (т.е. не имеет изломов), а среды 1 и 2 – изотропные. В общем случае следует обратиться к специальной литературе, например:
Вайнштейн Л.А., Журав С.М., Суков А.И., К расчету омических потерь на краях тонких металлических полосок. Докл. АН СССР, 1986, т.289, N6, с. 1338-1342. Курушин Е.П., Нефедов Е.И. Электродинамика анизотропных волноведущих структур. М.: Наука, 1983. – 223 с.
19