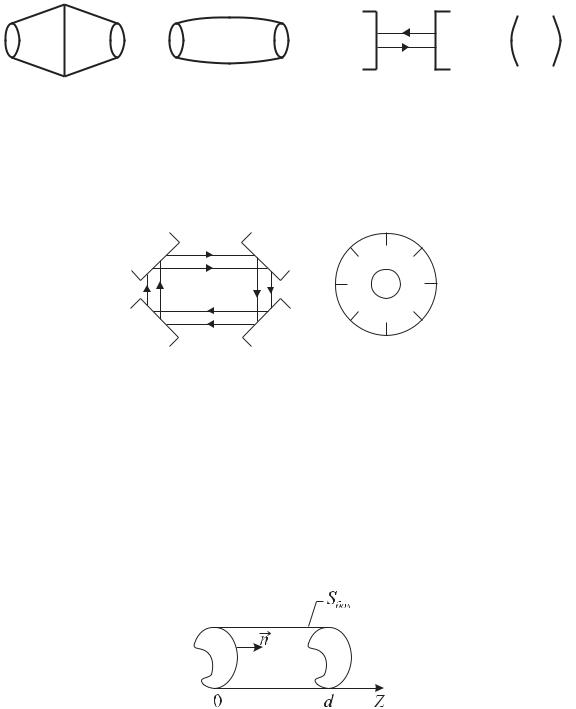
стенок получим соответствующие конфигурации открытых резонаторов, которые изображены на рис. 11.3

На рис. 11.4 показаны зеркальные открытые ОР: с плоскими (ОР Фаб- ри-Перо) и сферическими зеркалами.

На рис. 11.5 изображены ОР бегущей волны: четырехзеркальный резонатор гиротрона с Т-волной и резонансный блок магнетрона-амплитрона с замедленной Е-волной.

Рис. 11.5.

Далее мы остановимся на закрытых резонаторах, имея в виду их более простое математическое описание.

11.2 Поля в ОР как в отрезках регулярных волноводов с короткозамыкающими крышками

Пусть имеется отрезок регулярного волновода длиной d, закороченный с обеих сторон поперечными к оси волновода проводящими крышками (рис. 11.6).

Рис. 11.6.

В отрезке волновода в принципе могут распространяться все докритические типы волн в +Z и –Z направлениях. Обозначим их соответственно

Ev+ , Hv+ и Ev−, Hv− , причем, если поперечные крышки идеально проводящие, то на них должны выполняться условия

193

где значок «t» означает поперечную составляющую векторов поля. Представим

Здесь q1, q2 - обобщенные поперечные координаты (в общем случае - криволинейные), Гv - постоянная распространения v-го типа волн регулярно-

го волновода, Av± - комплексные амплитуды волн.

Учитывая, что обе волны v-го типа распространяются навстречу друг другу, т.е. Z- составляющие векторов Умова-Пойнтинга S0Z = 12 Et , Ht* для них противоположно направлены, имеем:

E−0vt = mEvt0 , H −0vt = ±Hvt0 .

Выбирая верхние знаки, получим

Используя граничные условия (11.1) при Z=0, имеем Av+ = Av− = A0 и, соответственно

Ervt = −2 jA0 Ervt0 (q1 ,q2 )siпГv Z , Hrvt = 2A&0 Hrvt0 (q1 ,q2 )cos Гv Z .

Учитывая далее условие (11.1) при Z=d, получаем резонансные (т.е. при которых возможен установившийся режим переотражений от крышек) длины волн:

причем Гvd=0 может удовлетворятся только для волн типа Е, имеющих составляющую Е, иначе в этом случае E=0.

194