
- •ЭЛЕКТРОДИНАМИКА И РАСПРОСТРАНЕНИЕ РАДИОВОЛН
- •ПРЕДИСЛОВИЕ
- •1.1. Интегральная формулировка УМ
- •1.3. Физическое содержание первого УМ
- •2.1. ГУ для тангенциальных составляющих векторов ЭМП
- •2.2. ГУ для нормальных составляющих векторов ЭМП
- •3.2. Баланс энергии в ЭМП. Теорема Умова-Пойтинга
- •4.2. Теорема о комплексной мощности
- •5.2. Электродинамические потенциалы
- •6.4. Общие свойства магнитных (Н) волн
- •6.7. Электрические (Е) типы волн в прямоугольном волноводе
- •6.8. Магнитные волны в прямоугольном волноводе
- •6.11. Магнитные (Н) волны в круглом волноводе
- •6.12. Потери и затухание волн в волноводах
- •7.3. Уравнения возбуждения регулярных волноводов сторонними токами
- •8.1. Неортогональные координатные системы
- •8.2. Дифференциальные операторы
- •8.4. Уравнение возбуждения произвольно-нерегулярного волновода сторонними токами
- •8.5. Самосогласованные нелинейные уравнения лампы бегущей волны О - типа
- •8.6. Уравнения возбуждения произвольно-нерегулярного коаксиального волновода
- •8.7. Уравнения возбуждения нерегулярных замедляющих систем
- •8.8. Нерегулярные волноводы с прямоугольным сечением.
- •8.9 Т-функции для решения двухточечных задач в теории нерегулярных волноводов
- •8.9.1 Т-функции
- •8.9.2 Взаимодействие Hoi волн в гофрированном волноводе с круговым сечением
- •9.3. Трансформирующие свойства отрезков линий передачи.
- •9.4. Короткозамкнутые и разомкнутые на конце отрезки линии передачи (шлейфы).
- •9.5. Частичное отражение волн в линиях передачи.
- •10.1. Понятие планарных линий передачи.
- •10.2. Симметричная полосковая линия
- •10.3. Несимметричная полосковая линия
- •10.4. Симметричная щелевая линия
- •10.5. Несимметричная щелевая линия
- •10.6.1 Общая формулировка метода
- •10.7. Копланарная линия передачи
- •10.8. Четная и нечетная моды в связанных полосковых линиях
- •11.2 Поля в ОР как в отрезках регулярных волноводов с короткозамыкающими крышками
- •11.3 Расчет полей в резонаторах с помощью потенциалов Герца
- •11.3.1 Прямоугольный резонатор
- •11.3.2. Цилиндрический резонатор
- •11.4 Добротность собственных колебаний в резонаторах. Внешняя и нагруженная добротности
- •12.2 Свойства собственных функций резонатора
- •12.3 Уравнение возбуждения резонатора
- •12.4. Способы возбуждения резонаторов
- •13.1. Расчет полей с помощью электрического вектора Герца
- •13.2. Анализ поля ЭЭИ в квазистатической (ближней) зоне
- •13.3. Анализ поля ЭЭИ в волновой (дальней) зоне
- •14.3. Анализ поля ЭМИ в волновой (дальней) зоне
- •18.2. Зоны Френеля. Область, существенная для распространения радиоволн
- •18.3. Дифракция электромагнитных волн от края непрозрачного экрана
- •19.2. Наклонное падение горизонтально-поляризованной волны на плоскую границу раздела двух сред
- •19.3. Наклонное падение вертикально-поляризованной волны на плоскую границу раздела двух сред
- •19.4. Отражение плоских волн от плоской границы среды с потерями
- •20.3. Поле вертикального вибратора над плоской отражающей поверхностью
- •20.4. Поле горизонтального вибратора, поднятого над плоской поверхностью земли на высоту h
- •20.7. Учет сферичности земной поверхности
- •20.9. Дифракция радиоволн вокруг сферической земной поверхности
- •21.2. Поглощение радиоволн в тропосфере
- •21.3. Рефракция радиоволн в тропосфере
- •22.2. Механизм ионизации и рекомбинации на больших высотах
- •22.3. Электронная диэлектрическая проницаемость ионизированного газа без учета столкновений электронов с ионами и нейтральными молекулами
- •22.5. Преломление и отражение радиоволн в ионосфере
- •22.6. Влияние магнитного поля Земли на распространение волн в ионосфере. Двойное лучепреломление
- •23.1 Уравнения движения электрона в форме Лагранжа.
- •23.2 Поступательная (трансляционная) симметрия
- •23.3. Азимутальная симметрия
- •23.4. Вращающиеся поля
- •23.5. Бегущие в направлении z волны
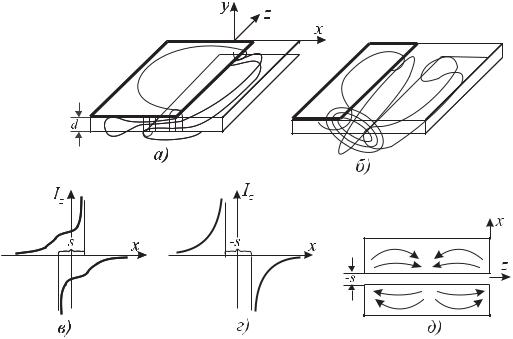
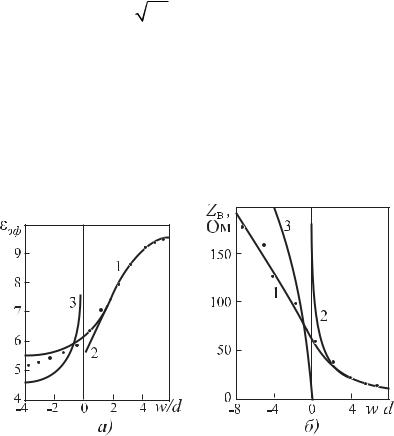
На рис.10.8,а приведены дисперсионные кривые волнового сопротивления и длины в СЩЛ с достаточно удаленными стенками экрана, а также результаты, рассчитанные по формулам (10.22) и (10.23). Влияние толщины металлических полуплоскостей на частотные характеристики волнового сопротивления и длины волны в СЩЛ показано на рис.10.8,б. Для узких щелей, как видно из кривых рис.10.8,б, необходимо учитывать толщину металлических полуплоскостей. Для сравнения на рис.10.8,б приведена кривая волнового сопротивления СЩЛ при нулевой толщине проводников.
10.5. Несимметричная щелевая линия
Несимметричная щелевая линия (НЩЛ) образуется металлическими полуплоскостями, нанесенными с разных сторон диэлектрической подлож-
ки. В зависимости от взаимного расположения полуплоскостей относительно друг друга возможны различные модификации НЩЛ: линия с перекрытием либо без перекрытия (рис.10.9, а, б), а также с нулевым перекрытием, когда края полуплоскостей находятся друг против друга.
Рис. 10.9.
В НЩЛ отсутствует кострукторско-технологическая особенность, связанная с реализацией узких проводников и щелей. Это позволяет выполнять НЩЛ с практически любой величиной волновых сопротивлений. Ограничения накладываются лишь наличием излучения энергии (открытая НЩЛ) со стороны больших волновых сопротивлений (большое расстояние между полуплоскостями), а со стороны малых – возможностью возникновения волн волноводного типа и поверхностных волн. Кроме того, НЩЛ обладает боль-
167
шой широкополосностью и простой конструктивной реализацией СВЧ элементов на ее основе в комбинации с НПЛ и СЩЛ, что во многом упрощает включение в нее (последовательно или параллельно) полупроводниковых приборов.
Поле НЩЛ описывается путем формулировки и решения интегрального уравнения с использованием метода Галеркина. Однако для простого и наглядного в физическом плане описания НЩЛ можно воспользоваться полуэмпирической моделью, полученной в результате обработки большого числа экспериментальных данных.
Результатом аппроксимации экспериментальных данных для эффективной диэлектрической проницаемости НЩЛ является формула:
ε |
эфф |
= (1/ 4)ε 3 + th(W / d − q) |
/ 2( |
ε −1) , |
(10.27) |
|
|
|
|
|
|
|
где q = (W / d)(2 −ε)+ ε(ε −1)/ 4 . |
|
|||
Волновое сопротивление, рассчитанное методом конформных отображений для ограничений ширины проводников и сопоставленное с экспериментальными данными, в результате аппроксимации приводит к следующей зависимости:
(10.28)
где k=0,515+0,5th(W/d-0,75). Сравнение расчетных данных с экспериментальными дает максимальную погрешность порядка 8% при S<0 и до 1% при
S>0.
На рис. 10.10 приведены экспериментальные данные (точки) по изучению НЩЛ, выполненной на подложке из поликора (ε = 9,8). Измерения проводились в длинноволновой области сантиметрового диапазона; результаты расчета по формулам (10.27) и (10.28) представлены кривой 1. Для сравнения
Рис. 10.10.
на этом же рисунке приведены результаты расчета НПЛ (кривая 2) и СЩЛ (кривая 3).
168
Анализ приведенных на рис. 10.10 результатов показывает, что НЩЛ обладает рядом интересных свойств. Во-первых, в случае перекрытия проводников (S>0) волновое сопротивление НЩЛ практически совпадает с НПЛ. Полное количественное совпадение наблюдается при величине перекрытия порядка полуволны и более. В случае без перекрытия проводников (S<0) НЩЛ по своим характеристикам в некоторой степени похожа на СЩЛ.
10.6. Модифицированный метод неортогональных рядов для расчета характеристик полосковых линий передачи.
10.6.1Общая формулировка метода
Вданном параграфе рассматривается модифицированный вариант метода неортогональных рядов, в котором системы неортогональных функций вводятся как решения семейств специальных краевых задач для области более простой формы, чем рассматриваемая. Эти семейства выбираются так, чтобы получаемые системы функций также обладали всеми необходимыми свойствами (полнота, линейная независимость), но учитывали геометрию и характер краевых условий. Они сложнее по форме и методике построения, но лучше передают особенности искомого решения. В связи с этим высокая точность достигается использованием небольшого их числа. В ряде задач для коэффициентов разложения по таким системам функций получаются системы линейных алгебраических уравнений 2-го рода, для которых гарантирована сходимость процесса редукции и вычислительная устойчивость. Таким образом, использование этих систем функций для разложения искомого решения эквивалентно процедуре регуляризации.
Описываемый подход реализуется на примере задачи математического моделирования процессов распространения электромагнитных волн в линиях передачи для интегральных схем диапазона сверхвысоких частот. Построение базисных функций выполняется аналитически при помощи метода задачи Римана-Гильберта.
Сформулируем метод сначала в общем виде. Для этого рассмотрим резонатор сложной формы в виде объема V (рис. 10.11 а, б), внутри которого будем решать уравнение Гельмгольца
|
|
2ϕ + p2ϕ = 0. |
(10.29) |
|||
Рассмотрим задачи двух типов: |
|
|||||
1. Найти собственные значения p2 , |
i =1,2,..., уравнения (3.1) при граничном |
|||||
|
|
|
|
i |
|
|
условии |
N |
|
||||
|
|
|
|
|
|
|
ϕ |
|
s = 0,S = S0 US′, |
S′ = USα . |
(10.30) |
||
|
||||||
|
|
|
|
|
α =1 |
|
2. Решать уравнения (3.1) при граничном условии |
|
|||||
|
|
ϕ |
|
s = f (Q), Q S . |
(10.31) |
|
|
|
|
||||
|
|
|
|
|||
169
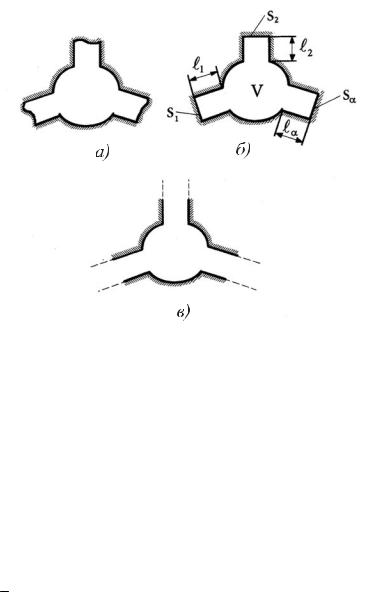
где: f(Q) - заданная функция.
Конфигурации резонаторов сложных форм (а, б) и соответствующая им ключевая задача для волнового трансформатора (в).
Мысленно удалим поверхность Sα и продолжим отрезки регулярных волноводных каналов до бесконечности. При этом придем к волноводному трансформатору (рис. 10.11 в), для каждого из каналов которого известны
полные системы собственных волн ϕm(α)e± jΓm(α )Zα зависят только от попереч-
Рис. 10.11.
ных для соответствующего канала координат), α=1, 2, ..., N; m=1, 2,... Введем систему функций {Φmβ }, каждая из которых представляет собой решение за-
дачи о возбуждении рассматриваемого волноводного трансформатора m-ой волной β-го канала. Внутри канала с номером α
Φmβ = Φαβm |
∞ |
+δαβϕm(α)e− jΓm(α )Zα |
|
= ∑Rnm(α)ϕn(α)e jΓn(α )Zα |
(10.32) |
||
|
n=1 |
|
|
где Rn(α) - постоянные коэффициенты, δαβ - символ Кронекера,
1 |
|
Γn = (p2 − χn2(α))2 |
, χn(α) есть n-е собственное значение двумерной области Sα. |
(В задаче 2 можно перейти, полагая p=0, к уравнению Лапласа. При этом в
(10.32) будет Γn(α)→jχn(α)).
170
Систему функций {Φmβ }будем использовать для разложения искомого
поля ϕ. Фактическое построение Φmβ , в частности вычисления Rnm(α) для мно-
гих практически интересных задач можно выполнить аналитически (при помощи метода Винера-Хопфа, переходом к задаче Римана и т.д.). в более сложных случаях для этой цели можно применить численно-аналитические методы.
Для первой задачи искомое поле в канале с номером α обозначим символом ϕα и представим разложением по функциям (10.32):
|
|
∞ |
N |
|
|
|
|
∞ |
N |
|
|
|
|
|
|
ϕα = ∑ ∑Cm(β )Φαβm |
= ∑ ∑Cm(β ) × |
|
(10.33) |
||||||||
|
|
m=1 β =1 |
|
|
|
|
m=1 β =1 |
|
|
|
|
||
|
|
∞ |
|
|
jΓ |
Z |
|
|
|
|
− jΓ |
Z |
|
× |
|
∑Rmα ϕ |
|
e |
+δαδϕ |
|
e |
|
|||||
|
α |
n(α ) α |
α |
m(α ) α |
|
||||||||
|
n( ) |
n( ) |
|
|
|
|
|
m( ) |
|
|
|
||
|
n=1 |
|
|
|
|
|
|
|
|
|
|
|
|
Для второй задачи разложения (10.33) модифицируется следующим образом:
∞N
ϕ= Φ0 + ∑ ∑Cm(β )Φmβ .
m=1 β =1
где Φ0 - частное решение уравнения (3.1), удовлетворяющее граничному условию (10.31) на поверхности S0.
Вычисление неизвестных коэффициентов Cm(β) производится при помощи граничных условий на поверхностях Sα. Будем использовать для этого метод моментов (для определенности рассмотрим его на примере задачи (1), заключающийся в переходе от условий (10.30) при zα=lα к цепочке соотношений ортогональности
∫ϕαϕn(α )dS = 0, α =1,2,...N; |
n =1,2,... |
(10.34) |
|||
Sα |
|
|
|
|
|
Подставляя в эти равенства (3.5) и интегрируя по Sα, получаем однородную |
|||||
систему линейных алгебраических уравнений для Cm(β) |
]= 0 . |
|
|||
∞ N |
|
|
|
||
∑ ∑Cm(β )[Rnm(α)e2 jΓn(α )lα +δαβδmn |
(10.35) |
||||
m=1 β |
|
|
|
|
|
Спектральный параметр p входит в (3.7) через Rm |
|
и Γ |
|
. Характеристиче- |
|
n(α) |
n(α) |
|
|
||
ские числа p отыскиваются из условий существования нетривиального решения системы (10.35).
Справедливо утверждение (теорема эквивалентности), что собственные значения задачи 1 и характеристические числа системы (10.35) совпадают, а собственные функции задачи 1 и нетривиальные решения системы (10.35)
связаны соотношением (10.33).
Следует отметить, что как изложенная выше схема решения, так и теорема эквивалентности остаются в силе и для других типов граничных условий: Неймана, 3-го рода и т.д. Однако в последнем случае, если коэффициент в граничном условии комплексный, рассматриваемая краевая задача стано-
171
вится несамосопряженной. Это может потребовать добавления в (10.33) присоединенных волн. Аналогичные схемы можно построить и в случае краевых задач для системы уравнений Максвелла.
Для обоснования различных вычислительных схем на основе функций (10.32) существенны вопросы о полноте и линейной независимости таких функциональных систем. Рассмотрим эти свойства.
Пусть все lα таковы, что некоторое действительное число p не является собственным значением задачи 1 в области V. Тогда система функций {Φmβ (p)}линейно независима на S' и полна в L2(S').
Свойство полноты будет доказано, если из условий
|
N |
|
∫ϕΦmβ *dS = ∑ ∫Φmβα* dS = 0, |
β =1,2,...N; m =1,2,...∞. (10.36) |
|
S ′ |
α =1Sα |
|
вытекает ϕ=0 на S'. Подставим в (10.36) разложение (10.33) и получим, что набор равенств (10.36) эквивалентен системе линейных алгебраических уравнений (символ” ” означает комплексное сопряжение).
N ∞ |
−2 jΓn(α )lα |
|
|
∑∑dn(α)Rnm(α* )e |
+ dn(β )δαβδmn = 0 . |
(10.37) |
α =1n=1
относительно
dn(α) = ∫ϕϕn(α)dS
Sα
Видно, что в условиях сделанного утверждения система (10.37) имеет только тривиальное решение: все dn(α)=0. При этом следует учесть, что матрицы систем (10.37) и (10.35) являются эрмитово-сопряженными, а область V
нерезонансна. Но из равенства dn(α)=0 следует ϕ=0 на S', т.к. системы {ϕn(α)}, n=1, 2, ... , для каждого α полны в соответствующих пространствах L2(Sα).
Для доказательства линейной независимости приравняем к нулю некоторое разложение по функциям Φmβ на S':
N ∞ ~ |
= 0 на S'. |
(10.38) |
∑ ∑Cm(β )Φmβ |
β =1m=1
Далее прейдем от (10.38) к эквивалентной цепочке соотношений ортогональ-
~
ности вида (10.34). Тогда для Cm(β ) получим вновь систему (10.35), которая,
как показано выше, имеет лишь тривиальное решение.
Аналогично можно рассмотреть также уравнение (10.29) со смешанными граничными условиями на S (условие Дирихле на S0, условие Неймана на S'). В предложении, что p не является собственным значением данной
|
m |
|
|
|
|
|
∂Φβ |
(p) |
|
||
краевой задачи, можно утверждать, что система функций |
|
|
|
линейно |
|
∂n |
|||||
|
|
|
|||
|
|
|
|
|
|
независима и полна в L2(S').
172
Рассмотрим теперь область ~ , ограниченную 0 и гладкими, но не
V
V
S
плоскими поверхностями Σα (рис. 3.1а). Пусть выполнены условия теорем о линейной независимости и полноте, доказанных выше, и Σα Sα= . Справедливо следствие, состоящее в том, что система функций {Φmβ (p)}полна в
L2(Σ'),
|
|
|
N |
|
|
|
|
|
|
Σ′ = UΣα . |
|
|
|
|
|
|
α =1 |
~ |
(Μ), |
~ |
|
|
|
|
|||
Это следствие доказывается следующим образом: пусть ϕ |
Μ V , - ре- |
|||||
шение уравнения (3.1), удовлетворяющее условию Дирихле на S0 и условию |
||||||
~ |
(Μ) |
|
Σ′ = f (Μ0 ), а f (Μ0 ) - заданная функция, Μ0 Σ′. |
|
|
|
|
|
|
||||
ϕ |
|
|
|
|||
|
|
|
~ |
f (Μ0 ) L2 |
(Σ′). Для лю- |
|
|
|
|
Функция ϕ(Μ) существует для произвольной |
|||
бого набора Σα имеется S' такая, что соответствующий ей объем V нерезонансен. Аналогично по теореме Купрадзе можно показать, что существует
F(Q) L2(S'), для которой |
|
|
|
|
~ |
′ |
′ |
, |
(10.39) |
ϕ |
(Μ)∫F (Q)G (Μ, Q)dSQ , |
Q S |
||
S ′
где G (M, Q) - функция Грина в области V, подчиненная указанным выше смешанным граничным условиям. Используя (3.11) и неравенство Буняков- ского-Шварца, получаем, что

 f (Μ0 )−
f (Μ0 )−
где ˆm(β )
C
n0 N |
ˆ |
m |
|
|
|
n0 N |
ˆ |
∂Φmβ |
|
|
|
|
|
|
|
||||||||||
∑ ∑Cm(β )Φβ |
(p) |
|
≤ const |
F(Q)− ∑ ∑ Cm(β ) |
|
|
|
|
(10.40) |
|||
|
∂n |
|
|
|||||||||
n=1β =1 |
|
|
|
L2 (Σ′) |
|
n=1β =1 |
|
|
L2 |
(Σ′) |
||
|
|
|
|
|
|
|
|
|
|
|||
- произвольные коэффициенты. Выбором n0 и подбором этих ко-
эффициентов правая часть (3.12) может быть сделана сколь угодной малой, откуда и вытекает утверждение следствия. Совершенно аналогично можно
доказать полноту {Φmβ (p)}в L2, на произвольной замкнутой поверхности внутри V.
Доказанное выше утверждение о полноте {Φmβ }позволяют использо-
вать эти функции для представления решений, в том числе в областях достаточно сложных некоординатных форм. для отыскания коэффициентов разложения по ним, кроме обычного метода моментов, можно использовать вариационные принципы, метод наименьших квадратов, коллокационные процедуры и т.д.
173
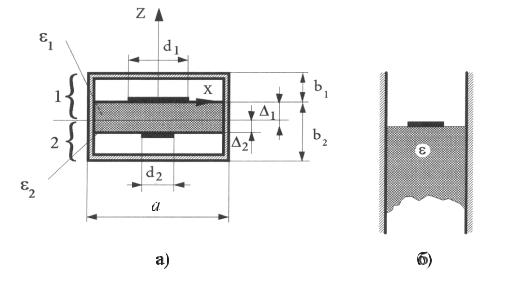
10.6.2 Расчет физических параметров полосковых линий передачи
Конфигурация рассматриваемой модели линии передачи показана на рис. 10.12а. Она является достаточно общей и позволяет исследовать ряд типов линий, широко применяемых в технике.
В квази -Т- приближении задача сводится к вычислению потенциала ϕ (x, y),
удовлетворяющего |
уравнению |
Лапласа |
2 ϕ = 0 |
в |
области |
|
|
|
xy |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Рис. 10.12. |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
x |
|
< a , − b |
≤ z ≤ b |
|
|
Граничные условия имеют вид |
|
|
|
|
|
|
||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||
|
|
|
2 |
2 |
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
± a |
, z |
|
|
|
|
|
|
|
(x,− b2 )=ϕ(x,b1 )= 0, |
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
ϕ |
|
|
|
|
=ϕ |
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
ϕ(x,−(∆ + ∆ |
|
)) |
|
|
|
|
|
|
d 2 = 0, ϕ(x,0) |
|
|
|
|
|
|
d1 =1. |
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
2 |
|
|
|
x |
|
|
|
|
|
|
|
|
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
≤ 2 |
|
|
|
|
≤ 2 |
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
Кроме того, должны быть выполнены условия непрерывности Z- |
d |
|
|||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
компонента вектора электрического смещения D = −ε ϕ |
при z=0 |
|
x |
≥ |
1 |
, |
|||||||||||||||||||||||||||||||||
|
2 |
||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
d2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
z=–∆1, z=–(∆1+∆2) |
|
|
x |
|
≥ |
|
(при этом ε=1 при z>0, |
z ≤ −(∆1 + ∆2 ), ε=ε1, при |
|||||||||||||||||||||||||||||||
|
|
||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
0 ≥ z ≥ −∆1, ε=ε2, при − ∆ ≥ z ≥ −(∆1 + ∆2 ). |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||
Наибольший прикладной интерес представляет погонная емкость линии, определяемая соотношением
174
|
|
|
d1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
C =ε |
|
|
2 |
|
|
|
|
ε |
∂ϕ |
|
|
|
|
|
− |
∂ϕ |
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
||||||||||||||||
0 |
|
∫d |
|
|
|
|
1 ∂z |
|
|
|
Z =−0 |
∂z |
|
Z |
=+0 |
dx , |
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
− |
1 |
|
|
|
|
|
|
|||||||||||||||
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
где ε0 - диэлектрическая проницаемость вакуума. |
|
|||||||||||||||||||||||
Через нее выражается ε |
|
= |
|
C |
|
, где C = |
lim C |
|
||||||||||||||||
|
|
C |
|
|
||||||||||||||||||||
|
эфф |
|
|
|
|
|
0 |
|
ε1, 2 →1 |
|
|
|||||||||||||
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|||
и волновое сопротивление Z |
|
|
=120πε−1 |
(C |
|
C )− |
|
|||||||||||||||||
В |
|
2 . |
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
0 |
|
|
0 |
|
|
|
|
||||||||
Конкретизируем для данной задачи способ построения базисных функ- |
||||||||||||||||||||||||
ций из п.10.6.1. Рассмотрим полосу |
|
x |
|
≤ |
α , − ∞ ≤ Z ≤ ∞ (рис. 10.12б) и по- |
|||||||||||||||||||
|
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
строим семейство решений краевых задач для уравнения Лапласа Um(X, Z), m=1, 2,... , при граничных условиях
|
a |
,Z |
|
|
= 0, Um (X ,0)= 0, |
|
X |
|
≤ |
d |
, |
|
|
|||
|
|
|
|
|
||||||||||||
Um ± |
2 |
|
|
|
|
2 |
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(10.41) |
||
|
∂Um |
|
|
∂Um |
|
|
|
|
|
|
|
|
|
|||
|
|
Z =+0 =ε |
|
Z =−0. |
|
|
|
|
||||||||
|
|
|
|
|
|
|
||||||||||
Потребуем, чтобы |
|
∂Z |
|
|
|
∂Z |
|
|
|
|
|
|
||||
|
|
|
|
lim [Um − cos(γ m x)eγ m Z ]= 0 , |
|
|||||||||||
lim Um =0 и |
|
|
||||||||||||||
Z →−∞ |
|
|
|
|
Z →−∞ |
|
|
|
|
|
|
|
|
|
|
|
где γ m = (2m +1)π . Функции Um(X, Z) можно представить в виде разложе- |
||||||||||||||||
a |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ний: |
|
|
|
|
|
∞ |
|
|
|
|
||||||
Um (X ,Z )= cos(γ m x)eγ m Z |
|
|
±γ p Z . |
|
||||||||||||
+ ∑C(pm) cos(γ p x)e |
(10.42) |
|||||||||||||||
|
|
|
|
|
|
p =0 |
|
|
|
|
||||||
(знаки “+” и “-” соответствуют областям Z >0 и Z< 0), а для коэффициентов |
||||||||||||||||
C(pm) получить из граничных условий (10.41) системы парных сумматорных уравнений вида
|
|
|
|
|
∞ |
|
|
(pm)cos(γ p x)= −cos(γ m x), |
x ≤ d , |
|
|
|||||
|
|
|
|
|
∑ C |
|
|
|||||||||
|
|
|
∞ |
p =0 |
|
|
|
|
|
|
|
2 |
|
(10.43) |
||
|
|
|
|
|
|
|
|
1 − ε cos(γ m x), x |
≥ d . |
|||||||
|
|
∑ C(pm)γ p cos(γ p x)=γ m |
||||||||||||||
|
|
p =0 |
|
|
|
|
1 + ε |
|
|
|
2 |
|
||||
Уравнения (10.43) могут быть точно решены методом задачи Римана- |
||||||||||||||||
Гильберта; в результате имеем |
|
|
|
|
|
|
|
|||||||||
|
|
|
1 |
|
|
|
p |
|
|
|
|
|
|
|
|
|
|
2 m + |
|
|
(−1) |
|
|
|
R |
|
|
|
|
|
|||
2 |
|
|
p |
|
|
|
||||||||||
C(pm) = |
|
|
|
|
|
|
Vpm −Vp−(m+1) − |
|
(Vσm |
−Vσ−(m+1)) |
−δ pm (−1)p , (10.44) |
|||||
|
|
|
|
1 |
|
R |
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
||||||
|
(ε +1) p + |
|
|
|
|
σ |
|
|
|
|||||||
2 |
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
175
где V m , V m , R |
|
, R |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
π(d − a) |
||
p |
- специальные функции аргумента U = cos |
, |
||||||||||||||||||||||||||||
p |
σ |
|
σ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
a |
|
выражаемые через полиномы Лежандра: |
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
(u)P (u)], p ≠ m; |
|||||||||||||||||||||||
|
|
|
|
V m = |
|
p +1 |
|
|
|
[P (u)P |
(u)− P |
|
|
|||||||||||||||||
|
|
|
|
2 |
(p − m) |
|
|
|||||||||||||||||||||||
|
|
|
|
p |
|
|
|
|
p |
|
m+1 |
|
|
|
p +1 |
|
|
|
m |
|
|
|||||||||
|
|
|
|
|
|
Vmm (u)= |
1 |
m+1 |
|
|
|
(u)Pk −m−1(u), m ≥ 0, |
|
|||||||||||||||||
|
|
|
|
|
|
|
∑ρm+1−k |
|
||||||||||||||||||||||
где ρ0 (u)=1, |
ρ1(u)= −u, |
|
|
|
|
|
2 k =0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
ρn (u)= Pn (u)− 2uPn−1(u)+ Pn−2 (u), |
n ≥ 2 ; |
|||||||||||||||||||||||||||||
|
|
|
|
|
|
|
R |
p |
= 1 P(u), R |
|
= π |
P |
|
(u); |
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
σ |
2 |
|
1 |
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
π |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
V m = − |
|
|
|
|
|
|
|
|
P |
1 |
(u)P |
|
(u) |
− P |
(u)P (u) . |
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
σ |
|
|
|
|
|
1 |
− |
|
m+1 |
|
|
|
|
|
1 |
|
m |
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
4 m |
+ |
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
2 |
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
Кроме того, введем семейство функций Vm(X, Z) удовлетворяющих уравнению Лапласа, граничным условиям (10.41), но с условиями на бесконечности вида
lim Vm = 0 и |
lim [Vm − cos(γ m x)e−γ m Z ]= 0 . |
|
|
Z →∞ |
Z →∞ |
|
|
Функции Vm(X, Z) даются разложениями |
|
|
|
|
∞ |
(pm)cos(γ p z)emγ p Z |
|
Vm (X ,Z )= cos(γ m z)e−γ m Z + ∑B |
(10.45) |
||
p =0
а коэффициенты B(pm) вычисляются аналогично и даются выражением
B(pm) =ε C(pm) −δmp (1 −ε). Функции (10.42) и (10.44) будут использованы для
разложения искомого потенциала ϕ . В соответствии с полученными в п. 10.6.1 результатами, они обладают требуемыми свойствами полноты.
Для построения алгоритма решения разобьем исследуемую область на две частичные подобласти:
область 1: |
|
|
|
x |
|
≤ a |
, − ∆ ≤ z ≤ b ; |
|
|||
|
|
|
|||||||||
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|||||||
область 2: |
|
x |
|
≤ a , |
− b ≤ z ≤ −∆ |
1 |
. |
||||
|
|
||||||||||
|
|
|
|
|
|
2 |
2 |
|
|||
|
|
|
|
|
|
|
|||||
Будем искать решение в виде (область 1) |
|
|
|||||||||
ϕ(X ,Z )=V (X , Z )+ ∑∞ [αm(1)Um(1)(X , Z )+ βm(1)Vm(1)(X , Z )] |
|||||||||||
m=0 |
|
|
|
||||||||
и (область 2) |
|
|
|
||||||||
ϕ(X ,Z )= ∑∞ [αm(2)Um(2)(a − x,−(z + ∆1 + ∆2 ))+ |
|||||||||||
m=0
+ βm(2)Vm(2)(a − x,−(z + ∆1 + ∆2 ))];
176
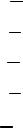
αm(j ), βm(j ) - неизвестные коэффициенты; Um(j ), Vm(j ) - функции (10.42), (10.44)
при d=d1, ε=ε1 для j=1 и d=d2, ε=ε2 для j=2; V(X, Z) - решение уравнения Лапласа, убывающее при z → ± ∞, удовлетворяющее условию
V (X ,0)=1, |
|
X |
|
≤ |
d1 |
, а в остальном - граничным условиям (10.41). Оно имеет |
|||
|
|
||||||||
|
|||||||||
вид |
|
|
|
2 |
V (X ,Z )= ∑∞ Ap cos (γ p x)e±γ p Z = |
||||
|
|
||||||||
|
|
|
|
|
|||||
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
p =0 |
||
|
|
|
|
|
|
∞ |
4(−1)p R |
||
|
|
|
|
|
|
= ∑ |
p |
cos(γ p x)emγ p Z . |
|
|
|
|
|
|
|
(2 p +1)R |
|||
|
|
|
|
|
|
p =0 |
σ |
||
Для нахождения коэффициентов αm(1), βm(1) следует наложить условия
непрерывности ϕ и z-компоненты D при z= –∆1, а также граничные условия для ϕ при z=b1, z= –b2. Тогда получим систему линейных алгебраических уравнений вида
|
ξ11 |
ξ12 |
0 |
0 |
|
α(1) |
|
ν1 |
|
|
|
|
|
|
|
||||||
|
ξ 23 |
|
|
|
|
|||||
|
0 |
0 |
ξ 24 |
|
β (1) |
|
0 |
|
|
|
|
−ξ33 |
|
= |
. |
(10.46) |
|||||
|
ξ31 |
ξ32 |
ξ34 |
α(2) |
ν2 |
|||||
|
ξ31 ξ32 − |
2I ξ33 ε2 ξ 44 |
|
β (2) |
|
ν2 |
|
|
||
|
|
|
ε1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
где α(j), β(j) - бесконечномерные векторы коэффициентов αn(j), |
βn(j), a ξij - |
|||||||||
матрицы следующей структуры: |
|
|
|
|
|
|
|
|||
ξmn11 =δmn + Cn(m) e−2γ nb1 ,
ξmn12 = (δmn + Bn(m) )e−2γ nb1 ,
ξmn31 = (δmn + Cn(m) )e−2γ n ∆1 ,
ξmn32 = δmn + Bn(m) e−2γ n ∆1 ,
ξ33 = −δ + C(nm) e−γ n (∆1 +∆2 ),
mn mn
|
|
|
|
|
|
|
|
|
ξmn34 = {−δmn e−γ n (∆2 −∆1 ) − |
|
|
n(m) e−γ n (∆1 +∆2 )}, |
|
||||||||||||||||||||||
|
|
|
|
|
|
B |
|
||||||||||||||||||||||||||||
|
|
|
|
|
|
44 |
|
|
ε |
2 |
|
−γ |
|
(∆ |
|
−∆ |
|
) |
|
|
|
|
(m) |
e |
−γ |
|
(∆ |
|
+∆ |
|
) |
, |
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
ξmn = |
|
−δmn e |
|
n |
|
2 |
|
1 |
|
+ Bn |
|
n |
|
1 |
|
2 |
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
ε1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Imn =δmn , ξ 23 , ξ 24 |
получаются из ξ11, ξ12 заменами |
|
|
|
|
|
|||||||||||||||||||||||||||||
|
|
(m) |
, |
|
|
(m) → |
|
|
(nm), |
|
(nm) |
и b1→ b1 - ∆1 - ∆2 (одна либо две черты над |
|||||||||||||||||||||||
|
|
|
|
|
|
||||||||||||||||||||||||||||||
|
|
|
|
|
C |
B |
|||||||||||||||||||||||||||||
C |
|
B |
|||||||||||||||||||||||||||||||||
|
n |
|
|
|
n |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
177
Cn(m), Bn(m) означают их принадлежность, соответственно, первой и второй
частичным областям). Коэффициенты ν1,2 в правой части (10.46) даются равенствами
ν1=–An e–2γnb1, ν2=–An e–2γn∆1,
Система (10.46) является Фредгольмовой, что следует из асимптотических оценок Cn(m), Bn(m), An. Для нее строго обоснован метод редукции.
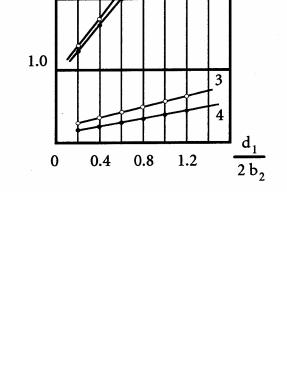
В качестве простейшего примера рассмотрим экранированную микрополосковую линию (рис. 10.13а).
Предельный переход к экранированной микрополосковой линии от более общей конфигурации 10.12а можно выполнить различными способами,
например: ε1→ ε2, d2→ a, либо ε1→ ε2, ∆1+∆2→ b2, либо ∆2→ 0, d2→ a (рис. 10.13б, в, г).
На рис.10.14 приведены результаты расчета погонной емкости микро-
Рис. 10.13.
полосковой линии методом неортогональных рядов (эти результаты нанесены кружками). Для сравнения взяты данные (сплошные линии), полученные методом полуобращения с использованием задачи Римана-Гильберта. На рисунке:
линия 1: |
b2 |
= 0.25; |
b1 + b2 |
= 0.5 ; ε=10.5; |
|
a |
a |
||||
|
|
|
178
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Рис. 10.14. |
|||||
линия 2: |
|
b2 |
= 0.1; |
|
b1 + b2 |
= 0.9 |
; |
ε=10.5; |
||||
|
a |
a |
||||||||||
|
|
|
|
|
|
|
|
|||||
линия 3: |
b2 |
|
= 0.25; |
|
b1 + b2 |
|
= 0.5 |
; |
ε=1.0; |
|||
|
|
a |
||||||||||
|
|
a |
|
|
|
|
|
|
||||
линия 4: |
b2 |
|
= 0.1; |
b1 + b2 |
|
= 0. |
ε=1.0. |
|||||
|
|
|||||||||||
|
|
a |
|
|
|
a |
|
|
|
|||
В табл. 10.1 приведены примеры характеристик полосковых линий, часто применяемых на практике
179
|
|
|
|
|
|
|
|
Табл.10.1 |
|
|
|
|
|
|
|
|
|
|
|
ε |
а, |
d1, |
b1, |
h, |
N |
I |
εэфф |
ZВ, |
|
|
мм |
мм |
мм |
мм |
4 |
|
|
Ом |
|
9.8 |
1 |
0.02 |
20 |
1 |
2 |
300 |
5.403383 |
136.3948 |
|
9.8 |
1.5 |
0.05 |
20 |
1 |
3 |
300 |
5.430295 |
118.5018 |
|
9.8 |
2 |
0.1 |
20 |
1 |
5 |
300 |
5.492849 |
103.9079 |
|
9.8 |
8 |
0.6 |
20 |
1 |
5 |
300 |
6.229931 |
64.07808 |
|
9.8 |
10 |
1 |
20 |
1 |
5 |
300 |
6.484238 |
50.78413 |
|
9.8 |
15 |
3 |
20 |
1 |
10 |
300 |
7.28545 |
26.13688 |
|
9.8 |
20 |
8 |
20 |
1 |
10 |
300 |
8.107649 |
12.14053 |
|
3.78 |
2 |
0.1 |
20 |
1 |
5 |
300 |
2.419478 |
156.5620 |
|
3.78 |
8 |
0.6 |
20 |
1 |
5 |
300 |
2.662139 |
98.02476 |
|
3.78 |
10 |
1 |
20 |
1 |
5 |
300 |
2.744443 |
78.06032 |
|
3.78 |
18 |
5 |
20 |
1 |
10 |
300 |
3.136074 |
28.01408 |
|
1 |
20 |
8.87 |
0.5 |
0.5 |
10 |
500 |
1 |
10.18 |
|
1 |
25 |
7.31 |
0.5 |
0.5 |
10 |
500 |
1 |
12.27 |
|
1 |
25 |
6.2 |
0.5 |
0.5 |
10 |
500 |
1 |
14.33 |
|
1 |
23 |
5.37 |
0.5 |
0.5 |
10 |
500 |
1 |
16.40 |
|
1 |
20 |
4.72 |
0.5 |
0.5 |
10 |
500 |
1 |
18.46 |
|
1 |
15 |
3.13 |
0.5 |
0.5 |
10 |
500 |
1 |
26.73 |
|
1 |
5 |
1.21 |
0.5 |
0.5 |
10 |
500 |
1 |
57.98 |
|
1 |
3 |
0.19 |
0.5 |
0.5 |
10 |
500 |
1 |
162.02 |
|
180
10.6.3Пример использования метода неортогональных рядов: расчет характеристик области сильной связи трехдецибельного
направленного ответвителя
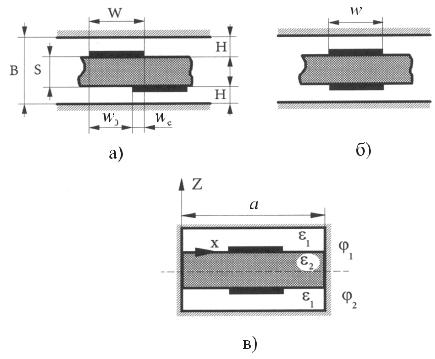
Для создания трехдецибельных направленных ответвителей (НО) на связанных полосковых линиях используются смещенные линии (рис. 10.15а). Полоса перекрытия НО более октавы реализуется каскадным соединением отрезков связанных линий с различной степенью связи в каждом каскаде. При увеличении числа каскадов в симметричном НО расширяется полоса рабочих частот и одновременно степень связи в его центральном каскаде. Следовательно, широкополосность симметричных НО ограничена возможностью реализации сильной связи.
Максимальная величина связи достигается при конфигурации нулевого смещения (рис. 10.15б), т.е., когда полоски расположены одна над другой.
Часто при проектировании НО на смещенных линиях пользуются формулами, полученными методом конформных преобразований, предполагая, что пространство внутри экрана заполнено однородным диэлектриком. Ис-
Рис. 10.15.
пользование прокладок из материалов с диэлектрической проницаемостью ε1, даже слабо отличающейся от проницаемости подложек ε2, ведет к ошибке в нахождении волновых сопротивлений честной и нечетной мод порядка 2-5%. Расчеты на ЭВМ показывают, что это приводит к увеличению девиации переходного ослабления относительно расчетного значения на 0,2-0,5 дБ. Кроме того, имеются ограничения на геометрические размеры связанных линий:
181

W |
|
|
W |
|
|
|
|
||
|
|
B |
|
|
|
|
|||
|
0 |
≥ 0.7; |
|
|
|
|
≥ 0.35 . |
||
S |
|
|
S |
||||||
|
|
|
|
|
|||||
|
|
|
1 |
− |
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
B |
|
||
Анализ этих ограничений показывает, что существует предел максимальных значений волновых сопротивлений, достоверно полученных таким методом. Поэтьому метод конформных преобразований не позволяет точно определить геометрические параметры линий для высоких значений волновых сопротивлений четной моды, необходимые для создания сверхширокополосных симметричных НО.
Расчет же с помощью метода неортогональных рядов не связан с каки- ми-либо ограничениями, накладываемыми на геометрию линий и характеристики материалов прокладки и подложек. Будем рассчитывать полностью экранированную модификацию линии (рис. 10.17в), что более удобно для применения метода, и при достаточно большом а не приводит к ощутимым погрешностям.
Эффективная диэлектрическая проницаемость и волновое сопротивление четной и нечетной мод вычисляется по формулам
|
++ |
|
ρ(ε)+ ρ12 |
(ε) |
; |
+− |
ρ(ε)− ρ12 |
(ε) |
|
|||
εэфф = |
|
|
|
εэфф = |
|
|
|
; |
||||
ρ(1)+ ρ |
(1) |
|
ρ(1)− ρ |
(1) |
||||||||
|
|
|
|
12 |
|
|
|
1 |
12 |
|
|
|
Z |
++ |
= Z0 |
[ρ(ε)+ ρ |
|
|
|
|
|
||||
|
|
(ε)][ρ(1)+ ρ (1)]; |
|
|
|
|||||||
|
|
|
|
|
12 |
|
12 |
|
|
|
||
Z |
+− |
= Z0 |
[ρ(ε)− ρ |
|
1 |
|
|
|
|
|||
|
|
(ε)][ρ(1)ρ (1)]; |
|
|
|
|||||||
|
|
|
|
|
12 |
|
12 |
|
|
|
||
где Z0 - волновое сопротивление вакуума;
ρ(ε)= C(ε), |
ρ |
(ε)= |
C12 (ε) |
; |
|
||||
ε0 |
12 |
ε0 |
|
|
|
|
|
||
C ++ (ε)= C(ε)+ C |
(ε), C +− (ε)= C(ε)− C (ε). |
12 |
12 |
Емкости C (ε) и C12(ε) определяются следующим образом:
−ε0 |
X 2 |
|
|
|
∂ϕ |
|
|
|
∂ϕ |
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|||||||||||||
|
∫ |
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
ε1 ∂z |
|
|
− ε2 ∂z |
|
|
|
|
|||||||||||||
C(ε)= V |
|
|
|
|
|
|
|
|
dx , |
||||||||||||
|
0 |
X1 |
|
|
|
|
|
|
|
|
Z →+0 |
|
|
|
|
|
|
Z →−0 |
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
ε0 |
X 2 |
|
|
|
|
∂ϕ |
|
|
|
|
|
|
|
∂ϕ |
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
∫ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
ε21 |
∂z |
|
|
|
|
− ε1 ∂z |
|
|
|
|
|||||||||||
C12 (ε)= V |
|
|
|
|
|
|
|
|
|
dx , |
|||||||||||
0 |
X1 |
|
|
|
|
|
|
|
|
Z →−S +0 |
|
|
|
|
|
|
|
Z →−S −0 |
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
182
где x = |
(a −W ) |
; |
x |
2 |
= |
(a +W ) |
|
; V0 - потенциал полоски. |
||
|
|
|||||||||
1 |
2 |
|
|
2 |
|
|
|
|||
|
|
|
|
|
|
|
||||
|
Поля ϕ1 и ϕ2 представим разложениями по неортогональному базису |
|||||||||
|
|
ϕ1(X , Z )=V (X , Z )+ ∑∞ αm(1)Um (X ,Z )+ ∑∞ βm(1)Vm (X , Z ), |
||||||||
|
|
|
|
|
|
|
|
|
m=0 |
m=0 |
|
|
ϕ2 (X ,Z )= ∑∞ αm(2)Um (a − x,−s − z)+ ∑∞ βm(2)Vm (a − x,−s − z), |
||||||||
|
|
|
|
|
|
m=0 |
|
m=0 |
||
где базисные функции Um(X, Z), Vm(X, Z) являются решениями ключевых задач электростатики (п.10.6.2) и имеют вид
Um (X ,Z )= cos(γ m x)eγ m Z + ∑∞ C(pm)cos(γ p x)eγ p Z ,
p =0
Vm (X ,Z )= cos(γ m x)e−γ m Z + ∑∞ B(pm)cos(γ p x)emγ p Z ,
p =0
а функция V(X, Z) представляется в виде
V (X ,Z ) ∞ Ap cos( p x)emγ p Z ,
= ∑ γ
p =0
где γ m = (2m + 1)π ; знаки «+» и «–» соответствуют областям ε1 и ε2. Выраже- a
ния для C(pm), B(pm), Ap приведены в п.10.6.2, а коэффициенты αm(1, 2), βm(1, 2) вычисляются из бесконечных систем линейных алгебраических уравнений второго рода с вполне непрерывным оператором. Эти системы решаются на ЭВМ методом редукции (усечения).
Втабл.10.2 приведены результаты расчета Z++,Z+– и величин ε+эфф+ и
ε+эфф− связанных полосковых линий с полной лицевой связью при заданных
геометрических размерах и величин εr |
материалов. Эти данные были ис- |
|||||||||||
пользованы |
для |
|
изготовления |
экспериментального |
макета |
|||||||
(Zсогл = (Z ++ Z +−)1/ 2 ). |
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
Табл. 10.2 |
|
ε1 |
ε2 |
Н, |
|
S, |
W, |
ε++ |
|
ε+− |
Z++, |
Z+–, |
Zсогл, |
|
|
|
мм |
|
мм |
мм |
эфф |
|
эфф |
Ом |
Ом |
Ом |
|
|
|
|
|
|
|
|
||||||
2.8 |
3.1 |
1.5 |
|
0.04 |
0.36 |
3.062 |
|
2.811 |
10.81 |
219.7 |
48.737 |
|
В табл.10.3, 10.4 приведены примеры расчета полосковых линий с полной лицевой связью при согласовании на 60 и 165 ОМ. Из табл. 10.4 видно, что при определенных соотношениях относительно диэлектрических прони-
183
цаемостей подложек и прокладки можно получить повышение волнового сопротивления четной моды.
Погрешность расчета волнового сопротивления и эффективной диэлектрической проницаемости линии методом неортогональных рядов определяется порядком редукции N. Следует отметить, что соотношения геометрических размеров рассматриваемой линии являются неблагоприятными с точки зрения сходимости метода редукции (малая толщина прокладки по сравнению с шириной полосок), поэтому порядок решаемой системы значителен. Сходимость метода редукции иллюстрируется табл.10.5. В качестве оценки абсолютных погрешностей величин, приведенных в табл.10.2, можно принять их приращения при увеличении N с 72 до 80.
Табл. 10.3
Примеры расчета полосковых линий с полной лицевой связью при согласо-
|
|
вании на 50 Ом: ε1=2.8; ε2=3; |
N =10; I=300 |
|
||||||
|
|
|
|
|
|
|
|
4 |
|
|
а, |
d1, |
|
∆, |
b1, |
ε++ |
ε+− |
|
Z++, |
Z+–, |
Zсогл, |
мм |
мм |
|
мм |
мм |
эфф |
эфф |
|
Ом |
Ом |
Ом |
|
|
|
|
|||||||
4 |
0.37 |
|
0.04 |
1.5 |
2.9788 |
2.8054 |
|
10.7665 |
226.831 |
49.4184 |
4 |
0.41 |
|
0.05 |
2 |
2.9769 |
2.8083 |
|
11.6774 |
218.437 |
50.4836 |
4 |
0.41 |
|
0.05 |
1.5 |
2.9767 |
2.8086 |
|
11.6607 |
205.127 |
48.9073 |
2 |
0.2 |
|
0.02 |
2 |
2.9804 |
2.8044 |
|
10.1102 |
250.613 |
50.3364 |
2 |
0.2 |
|
0.02 |
1.5 |
2.9801 |
2.8044 |
|
10.1097 |
248.379 |
50.1102 |
6 |
0.42 |
|
0.06 |
2 |
2.9742 |
2.8118 |
|
13.0443 |
204.293 |
51.6224 |
|
|
|
|
|
|
|
|
|
|
|
Табл. 10.4
Примеры расчета полосковых линий с полной лицевой связью при согласо-
вании на 165 Ом; ∆=1мм, b1=20мм, |
N =10; I=300; ε1=1 |
|||||||
|
|
|
|
|
|
4 |
|
|
а, |
ε2 |
d1, |
ε++ |
ε+− |
|
Z++, |
Z+–, |
Zсогл, |
мм |
|
мм |
эфф |
эфф |
|
Ом |
Ом |
Ом |
|
|
|
|
|||||
10 |
1 |
1.2 |
1 |
1 |
|
86.0743 |
315.313 |
164.744 |
10 |
1.2 |
0.95 |
1.139 |
1.041 |
|
89.217 |
312.415 |
166.93 |
10 |
1.35 |
0.915 |
1.2435 |
1.0736 |
|
86.147 |
305.871 |
162.326 |
10 |
1.5 |
0.903 |
1.351 |
1.107 |
|
86.4038 |
315.414 |
165.08 |
10 |
1.7 |
0.89 |
1.487 |
1.145 |
|
85.53 |
322.078 |
165.97 |
10 |
1.85 |
0.7 |
1.603 |
1.212 |
|
88.85 |
309.711 |
165.088 |
9 |
2 |
0.6 |
1.652 |
1.226 |
|
89.415 |
288.257 |
160.545 |
8 |
5 |
0.3 |
3.260 |
1.8743 |
|
97.775 |
279.881 |
162.006 |
Табл. 10.5
184

Иллюстрация сходимости метода редукции
|
|
|
|
|
|
|
Z++, |
|
ε1 |
ε2 |
N |
I |
ε++ |
ε+− |
Z+–, |
||
|
|
|
|
эфф |
эфф |
Ом |
Ом |
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
2.8 |
3.1 |
24 |
500 |
2.974 |
2.821 |
|
27.099 |
203.276 |
2.8 |
3.1 |
32 |
500 |
2.990 |
2.816 |
|
20.498 |
210.518 |
2.8 |
3.1 |
40 |
500 |
3.007 |
2.813 |
|
16.469 |
214.910 |
2.8 |
3.1 |
48 |
500 |
3.023 |
2.812 |
|
13.991 |
217.492 |
2.8 |
3.1 |
56 |
500 |
3.038 |
2.811 |
|
12.483 |
218.899 |
2.8 |
3.1 |
64 |
500 |
3.049 |
2.811 |
|
11.589 |
219.527 |
2.8 |
3.1 |
72 |
500 |
3.056 |
2.811 |
|
11.081 |
219.721 |
2.8 |
3.1 |
80 |
500 |
3.062 |
2.811 |
|
10.8109 |
219.715 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Рис. 10.16.
Табл.10.6
Зависимость точности решения от числа слагаемых при вычислении базисных функций
|
|
|
|
|
|
Z++, |
|
ε1 |
ε2 |
N |
I |
ε++ |
ε+− |
Z+–, |
|
|
|
|
|
эфф |
эфф |
Ом |
Ом |
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
2.8 |
3.1 |
80 |
200 |
3.062 |
2.809 |
10.995 |
229.270 |
2.8 |
3.1 |
80 |
300 |
3.062 |
2.810 |
10.901 |
224.364 |
2.8 |
3.1 |
80 |
400 |
3.062 |
2.811 |
10.851 |
221.783 |
2.8 |
3.1 |
80 |
450 |
3.062 |
2.811 |
10.829 |
220.627 |
В качестве примера была поставлена задача разработки симметричного НО в диапазоне частот 140-1280 МГц (коэффициент перекрытия χ=9,1) с переходным ослаблением A=3±1 дБ. Для изготовления подложек использовался флан (ε1=2.8) толщиной Н=1,5 мм, для прокладки - полиамид (ε2=3.1) толщиной S=0,004 мм. Общая длина области связи НО 18,6 см. для уменьшения геометрических размеров НО область связи была выполнена П-образной формы (рис.10.18).
Частотная характеристика переходного ослабления НО, измеренная на панорамном измерителе КСВ, приведена на рис. 10.17.
185
