2.2 Теорема о дивергенции.

Теорема о дивергенции является обобщением известной теоремы Остроградского-Гаусса на случай тензоров ранга выше 1-го.

Фомула Остроградского-Гаусса связывает поверхностный и объемный интегралы:

В принятой нами форме записи эта формула примет вид:

Теорема о дивергенции (без доказательства):

(32)

где --- тензор произвольного ранга.

В частности, для тензора 2-го ранга справедливо равенство:

(33)

Резюме section 3.

1. Приведена тензорная (покомпонентная) форма записи векторных дифференциальных операций: 2. Векторные дифференциальные операции обощены на случай тензоров любого ранга. 3. Сформулирована теорема о дивергенции, являющаяся обобщением теоремы Остроградского-Гаусса. Теорема о дивергенции связывает интеграл по поверхности некоторой области пространства от тензора произвольного ранга с интегралом по объему этой области от дивергенции данного тензора.

3 Приведение симметричного тензора 2-го ранга к каноническому виду.

В МСС фундаментальное значение имеют тензоры 2-го ранга. Поэтому рассмотрим более подробно основные свойства таких тензоров.

3.1 Симметричные и антисимметричные тензоры.

Если при изменении мест индексов тензор не изменяется, то такой тензор называется симметричным, а если при такой операции тензор меняет знак, то --- антисимметричным. (Например, символ Кронекера --- симметричный тензор, а тензор Леви-Чивиты --- интисимметричный по любой паре индексов).

Произвольный (смешанный) тензор всегда можно представить в виде суммы симметричного и антисимметричного тензоров:

Очевидно, что: --- симметричен: , а --- антисимметричен: .

Заметим, что свертка симметричного тензора с тензором Леви-Чивиты равна нулю:

Справедливо и обратное: Если , то Это легко проверить, подставив в условие

3.2 Главные направления и главные значения тензора.

Пусть --- некоторый симметричный тензор. Рассмотрим свертку тензора с вектором :

(34)

Выражение (152) ставит в соответствие каждому вектору dgjkyt jghtltktyysq dtrnjh , компоненты которого --- линейные функции компонент .

Выражение (152) можно рассматривать как действие линейного оператора на вектор , которое пораждает вектор Симметричность означает, что задаваемый им оператор --- самосопряженный. Действительно:

Из линейной алгебры известно, что для линейного самосопряженного оператора можно найти собственные значения и собственные векторы, которые достаточно полно его характеризуют. Найдем соответствующие объекты для симметричного тензора второго ранга и рассмотрим их свойства.

Зададимся вопросом о существовании таких векторов, свертка с которыми тензора изменяет лишь их длину, но сохраняет направление:

(35)

Выражение (170) является фактически задачей на отыскание собственных векторов и собственных значений оператора .

Условие (170) представляет собой систему линейных алгебраических уравнений относительно его можно переписать как:

(36)

Для того, чтобы (171) была бы нетривиально разрешимой, необходимо, что бы:

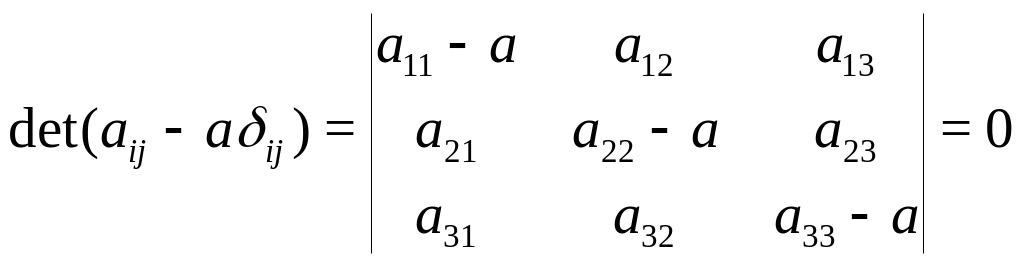(37)

Или:

(38)

где

(39)

(40)

(41)

Уравнение (122) (или (121)) называется вековым уравнением. Выражение для представляет собой свертки тензора , т.е. являются скалярными и , следовательно, не изменяется при преобразовании системы координат (в которой записан тензор ). Поэтому величины называют инвариантами тензора .

Вековое уравнение являетсякубическим уравнением и, следовательно, иммет три корня. Можно показать, что в случае симметричного тензора все три решения (122) --- вещественные. Действительно, пусть решение (122):

. Ему соответствует вектор . Подставив и в (171) и сравнив действительные и мнимые части, найдем:

(42)

(43)

В силу симметричности :

Следовательно: Т.к. и не могут быть одновременно равны нулю ( в этом случае ), приходим к выводу, что , т.е. решение векового уравнения --- вещественное.

Будем обозначать решения векового уравнения как , или . Величины являются собсбвенными значениями оператора . В терминах тензорного анализа называются глаными значениями тензора .

Главные значения , являясь решениями векового уравнения (122), представляют собой комбинацию инвариантов тензора . Поэтому ясно, что главные значения тензора также являются его инвариантами.

Зная , можно легко определить соответствующие им напряжения векторов , удовлетворяющих (170).

Действительно, из (171) имеем:

(44)

(45)

И очевидное условие:

Выражая из первых двух уравнений и через , получим:

и Учитывая последнее условие, найдем :

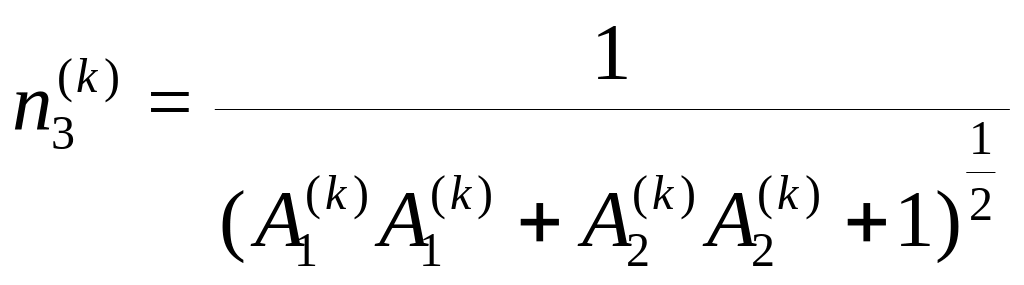
Найденные таким образом направления , вдоль которых "действие" тензора на векторы сводится просто к умножению этих векторов на , называются главными напрвылениями тензора . Векторы являются собственными векторами оператора .

Если все три главных значения тензора различны, то его главные направления взаимно ортогональны. Покажем это. Справедливы равенства:

Следоваетльно:

Поскольку , находим, что . Следоваетльно и ортогональны. Замечание. Можно показать, что если два главных значения тензора равны между собой, то все направления, лежащие в плоскости, ортогональной главному направлению, отвечающему третьему главному значению, не равному двум другим, являются главными. Т.е. если , то все направления в плоскости нормальной к , являются главными. Если все три главные значения тензора совпадают, то любое направление в пространстве является главным. Сделанное замечание означает, что при любом соотношении главных значений тензора всегда можно выбрать три взаимно ортогональных главных направления.