1.4.12. Трехслойные разностные схемы

Рассмотрим краевую задачу для уравнения гиперболического типа вида:

. (1)

. (2)

начальные условия:

. (3)

. (4)

Согласование начальных и граничных условий:

;

.

Считаем, что введена сетка:

.

Будем применять непосредственную аппроксимацию, так как уравнение с постоянными коэффициентами.

Так как в левой части вторая производная по времени, то понадобится шаблон, содержащий три соседних узла по времени.

. (5)

Непосредственным разложением в ряд Тейлора в окрестности точки до членов порядка О(h⁴), O(τ⁴) можно убедиться, что на решении задачи (1-4) погрешность аппроксимации для разностного уравнения (5) есть О(h²+τ²).

Также является очевидным аппроксимация граничных условий (2) и начального (3).

Заслуживает внимания аппроксимация уравнения (4). Использование непосредственной аппроксимации:

.

не позволяет получить порядок аппроксимации больше чем .

Сформулируем задачу для погрешности:

. (*)

. (**)

. (6)

В силу гладкости функции имеет место тождество:

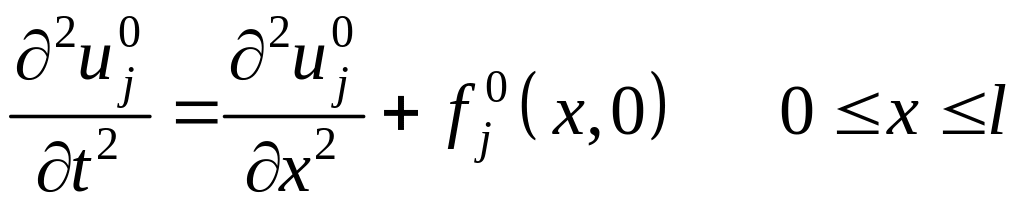. (7)

С другой стороны, справедливо предельное равенство:

.

Заменим функцию в правой части (7) на , получим:

. (8)

Выполним непосредственную аппроксимацию правой части равенства (8).

. (9)

Подставим (9) в (6):

.

.

Хотелось бы, чтобы невязка обращалась в ноль.

Вместо начального условия (4) будем использовать такой дискретный аналог:

.

Если теперь повторить предыдущие рассуждения, т.е. сформулировать задачу для погрешности, то она будет иметь вид:

.

Исследование устойчивости методом гармоник однородного уравнения с нулевыми граничными условиями. Необходимое условие устойчивости

Исследуем устойчивость схемы уравнения (1) методом гармоник.

.

Будем искать решение в виде:

,

где - мнимая единица, - номер узла по пространству.

.

Подставим (2) в (1), получим:

.

,

так как ,

то получаем:

;

, ;

, .

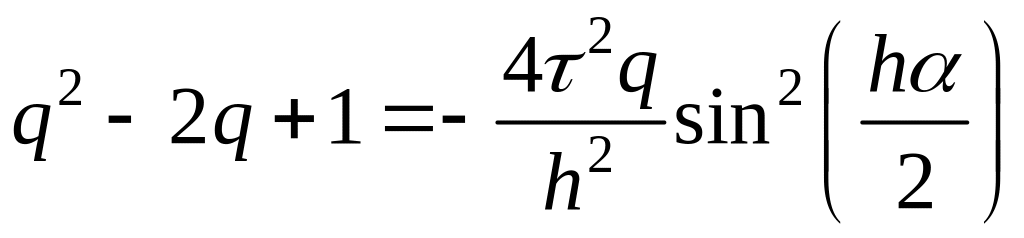Рассмотрим случай, когда подкоренное выражение неотрицательно, корни действительны и имеют вид: , тогда по теореме Виета: .

Если , тогда , следовательно, в этом случае схема не устойчива.

Тогда решение ищется в виде:

.

Следовательно, один возможный случай, когда модули корней совпадают, и они комплексные, т.е. подкоренное выражение (дискриминант) неположителен.

.

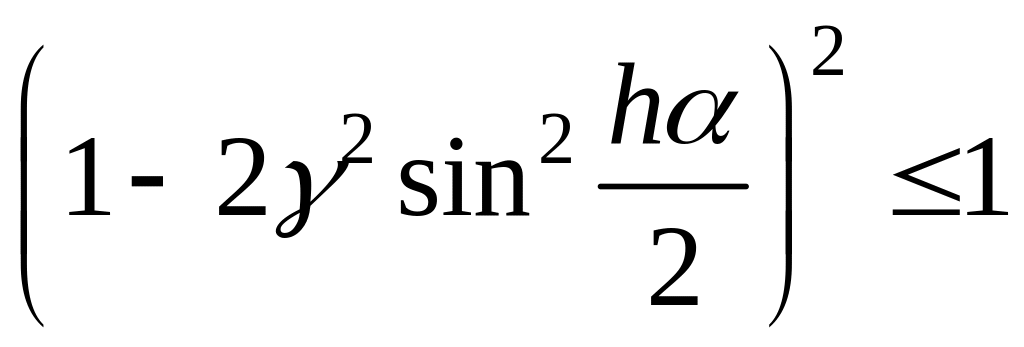
Достаточным условием выполнения этого неравенства является выполнение ,

то есть .

Условие

- условие Фридрихса– Куранта- Леви.

1.4.13. Примеры трехслойных разностные схем для уравнения теплопроводности

Возникает идея повысить точность аппроксимации для уравнения теплопроводности до за счет использования трехслойных схем.

Минимальный шаблон, обеспечивающий такую точность включает в себя точки: .

Так как аппроксимация граничных условий очевидна, то займемся разностными аналогами уравнения (1).

. (1)

. (2)

. (3)

Согласование начальных и граничных условий:

.

1) абсолютно не устойчивая схема.

Схема имеет точность .

_______________________________________________________________________

‼ Методом гармоник показать, что данная схема неустойчива.

_______________________________________________________________________

Рассмотрим формальную замену

.

С учетом ее рассмотрим схему вида:

2)

_______________________________________________________________________

1. ‼ Методом гармоник показать, что данная схема неустойчива;

2. ‼ получить оценку ;

3. ‼ построить непрерывный аналог данной схемы сохранив члены имеющие порядок малости .

_______________________________________________________________________