Введение в метод конечных элементов
Метод конечных элементов носит название вариационно-разностного метода. Реже встречается его другое название как проекционно-сеточный метод.
Этот метод применяют в случае сложной геометрии области, где ищется решение задачи, также является наиболее естественным, когда исходная задача имеет вариационную формулировку.
§1
Кусочно-линейные восполнения сеточных функций.
Фактически с кусочно-полиномеальными восполнениями мы имели дело при рассмотрении интерполирования, когда разговор шел о сплайнах.
Поставим задачу.
Пусть
- непрерывная функция на отрезке
.
Построим, в общем случае, не равномерную
сетку
.
Пусть в узлах сетки заданы значения
функции
.
Необходимо
построить кусочно-линейную, т.е. линейную
на каждом отрезке, функцию
,
которая в узлах сетки совпадает с
исходной функцией
,
т.е.
.
Рассмотрим два способа построения неизвестной функции.
1
-й
способ построения функции
.
.
(1)
,
,
.
Функция
не имеет производных в точках
,
но в точках
имеются односторонние производные и
можно разумным способом доопределить
полную производную в этих точках.
2-й способ построения функции .
Этот способ связан с введением базисных функций.
П
остроим
базис.
(2) 
(3) 
.
___________________________________________________________________________________________________
‼ Доказать,
что построенная система функций линейно
не зависима, т.е. любая линейная комбинация
равна нулю только тогда когда все
коэффициенты равны нулю на отрезке
[a,b].
Показать, что все функции базиса
квадратично интегрируемы, т.е.
.
___________________________________________________________________________________________________
Построенная система функций является базисом в классе кусочно-линейных функций, определенных на отрезке [a,b] у которых углы наклона могут меняться только в узлах сетки.
Очевидно, что
(4) 
.
Особо
выделим случай финитных функций:
,
тогда:
(5) 
.
В дальнейшем нам пригодятся производные, вычислим их.
(6) 
Удобство формул (2), задающих базисные функции состоит в том, что носитель функции составляет существенно малую часть от области определения функции.
Для дальнейшего нам потребуются леммы, которые позволяют оценить среднеквадратичное уклонение функции от в зависимости от гладкости функции и шагов сетки.
Лемма 1
Пусть
функция
,
т.е.
.
Тогда имеет место неравенство: (7) 
.
Доказательство:
Рассмотрим
на интервале
выражение вида
.
.
Итак, получено равенство:
(8) 
.
Возведем равенство (8) в квадрат и проинтегрируем.
(9) 
.
Оценим следующее выражение:
применим
неравенство Коши – Буняковского:
.
Итак, была получена оценка
.
Вернемся к равенству (9).
.
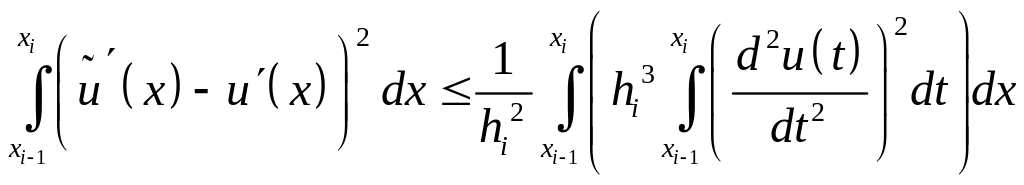Из последнего неравенства получаем,
.
Взяв
,
затем суммируя полученное равенства
по
,
мы получаем неравенство (7).
Лемма 2 Оценка среднеквадратичного отклонения функции от .
Пусть функция , т.е. . Тогда имеет место оценка:
(10) 
.
Доказательство:
Имеет место тождество
откуда следует
равенство (10).
___________________________________________________________________________________________________
‼ Получить
аналог оценок (7) и (10) в равномерной
метрике
.
___________________________________________________________________________________________________
§2