3. Свойства разностных эллиптических операторов

Рассмотрим задачу Дирихле для уравнения Пуассона.

В области требуется найти решение уравнения:

(1) ,

если заданы граничные условия:

(2)

Будем предполагать необходимую гладкость функций правых частей (1) и (2).

Для аппроксимации задачи (1), (2), область покроем равномерной сеткой с шагами по оси Ох₁ и по оси Ох₂ .

.

Внутренностью сетки будем называть множество точек:

,

граничными узлами:

.

Будем использовать пятиточечный шаблон, включающий в себя точки:

.

(3) .

(

4) .

Рассмотрим задачу на собственные значения.

Сразу считаем, что . Если это не так, то за счет переопределения в приграничных узлах этого всегда можно добиться

Введем оператор , .

Рассмотрим узлы, лежащие на первой линии снизу, т. е. .

Для узлов « » на PQ :

;

Слагаемое перенесем в правую часть, получим:

.

Для задачи (3), (4) спектральная задача с однородными граничными условиями имеет вид:

(5) ,

(6) .

Решение задачи будем искать в виде:

(7) .

Граничное условие (6), если справедливо (7) будет записано:

, т. к. .

Аналогично,

.

Итак, граничные условия (6) принимают вид:

(8)

Подставим (7) в (5)

, разделим на , получим:

.

.

Поскольку не зависит от , а не зависит от , то обе части (9) не зависят ни от , ни от , следовательно:

(10) 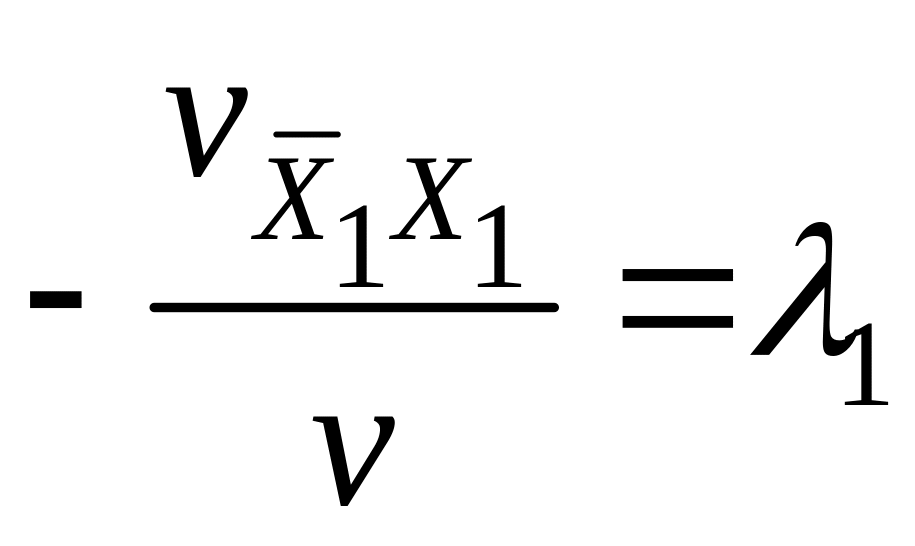, (11) , (12) .

Таким образом, мы получаем две задачи:

(13) , (14) ,

Займемся задачей (13).

, т.е. .

В параграфе 2 главы III было получено:

(15) ,

и набор собственных функций

(16) .

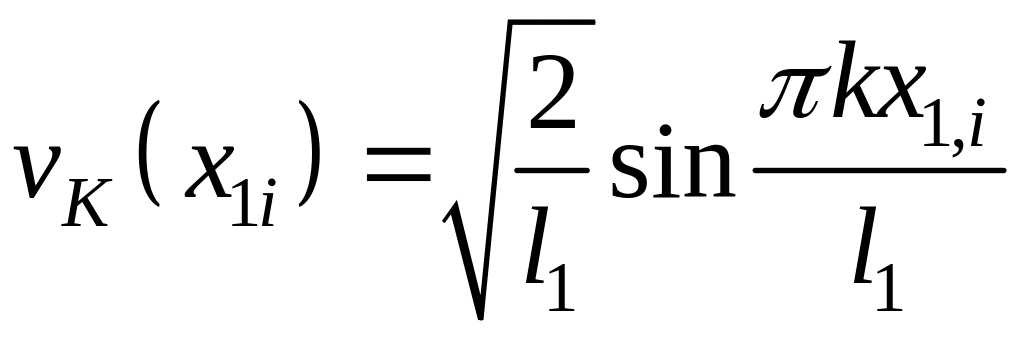Число собственных значений и собственных функций равно .

Займемся задачей (14).

По структуре она эквивалентна предыдущей задаче и имеет решение:

(17) ,

и набор собственных функций

(18) .

Учитывая соотношения (15), (16), (17), (18), а также (7), (12) получаем решение поставленной спектральной задачи (5), (6):

(19) ,

и набор собственных функций

(20)

Также как и в одномерном случае, приведем приближенные оценки для максимального и минимального собственного значений.

Общее число собственных значений и собственных функций равно .

(21) .

Приведем более “культурную” оценку для .

(22) .

Собственные функции, задаваемые (20) образуют ортонормированный базис. Этот факт можно проверить, введя в гильбертовом пространстве на множестве финитных функций скалярное произведение.

, , тогда скалярное произведение введем следующим образом:

(23) , где - сеточные функции.

Т.е. попарные произведения функций и .

(24) .

Справедливы оценки:

(25) , где получаются по формулам (21) и (22) или путем непосредственным подставлением .

(26)

___________________________________________________________

‼ 1) Используя представление (20) и определение скалярного произведения (23) докажите (24).

2) Используя оценки (21), (22) оценить энергию разностного оператора Лапласа .

3) Доказать самостоятельно (27).

План доказательства.

1. Из (25) следует, что положительно определен в пространстве финитных сеточных функций.

2. Используя вторую разностную формулу Грина можно доказать самосопряженность оператора , т.е. (26).

___________________________________________________________