Модуль 2 Разностные методы решения задач прикладной механики
ОГЛАВЛЕНИЕ
МОДУЛЬ 2. РАЗНОСТНЫЕ МЕТОДЫ РЕШЕНИЯ ЗАДАЧ МЕХАНИКИ ПРИКЛАДНОЙ МЕХАНИКИ………203
Комплексная цель модуля…………………………………………………………………..203
Введение…………………………………………………………………………………….203
Система уравнений движения вязкого сжимаемого теплопроводного
газа…………………………………………………………………………………………..204
Разностные схемы для модельных уравнений……………………………………………...235
Методы построения схем повышенного порядка аппроксимации………………………...242
Разностные схемы для системы уравнений газовой динамики……………………………247
Разностные схемы для полной системы уравнений Навье-Стокса………………………...257
Заключение……………………………………………………………………..280
Проектное задание………………………………………………………………………….281
Тест рубежного контроля………………………………………………………………..283
Применяются основные методы теории разностных схем для построения и исследования задач механики. В качестве дискретных моделей рассматриваются схемы, аппроксимирующие систему уравнений Навье-Стокса и ее упрощенные аналоги.
Комплексная цель модуля
Изучить приложения теории разностных методов. Механика жидкости и газа один из разделов прикладной математики в котором широко используют численные расчеты. Помимо исследования основных свойств дискретных моделей появляются новые свойства разностных схем, характерные для задач механики.
Введение
Вычислительная механика представляет один из современных разделов прикладных численных методов.
В модуле для различных физических моделей строятся разностные аналоги. Исследуются свойства построенных дискретных уравнений. Выделяются классы разностных схем второго порядка аппроксимации, классы безусловно устойчивых разностных схем.
Основные разделы модуля (с четвертого по седьмой) содержат конечно-разностные методы решения задач прикладной механики. Определяются основные понятия теории разностных схем и исследуются наиболее распространенные в механике разностные и итерационные схемы решения стационарных и нестационарных задач. Исследование проведено сначала для модельных уравнений, а затем обобщено на системы одномерных и многомерных уравнений газовой динамики, полные и упрощенные системы уравнений сжимаемого теплопроводного газа.
Система уравнений движения вязкого сжимаемого теплопроводного газа
Система уравнений, описывающая движение газа или жидкости основывается на законах сохранения (массы, импульса, энергии).
1. Закон сохранения масс. Уравнение неразрывности.
(1)
2. Закон сохранения импульса. Уравнение движения.
,
где
-поверхностные
силы,
-объемные
силы.
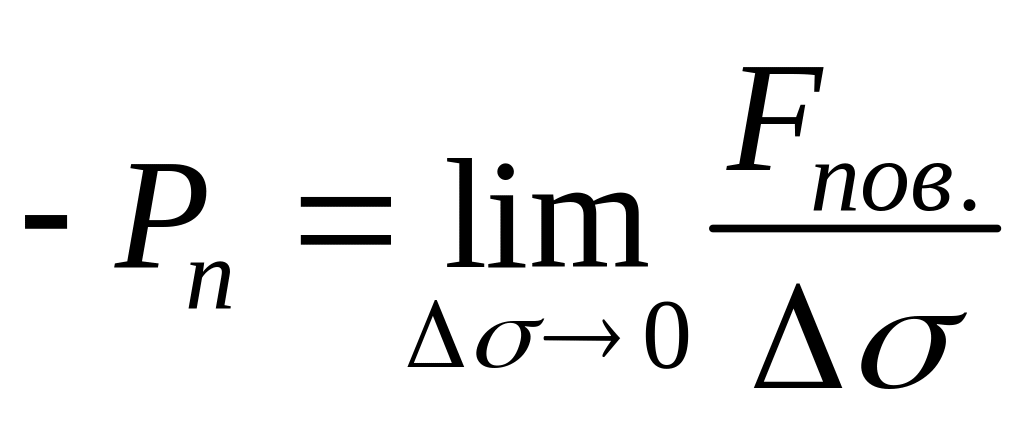– плотность
поверхностных сил.
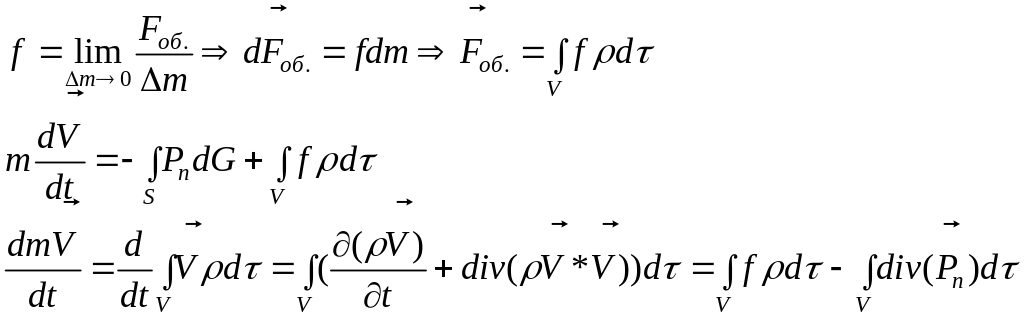
(2)
3. Уравнение энергии (закон сохранения энергии).
Используем первый закон термодинамики:
,
где
– внутренняя энергия,
–
давление,
–
энтропия.
– полная энергия
(3)
– величина теплового
потока.
– внешние источники.
,
– коэффициент теплопроводности.
Система уравнений
(1) – (3) неполная. Термодинамическое
равновесие описывается пятью функциями:
.
Поэтому добавляем уравнения состояний.
,
,
(4)
,
,
(5)
,
,
(6)
– используется
наиболее часто.
.
,
– тензор скоростей деформации,
– статистическое давление,
– вязкости,
– единичный тензор.
.
Для воды:
,
для воздуха:
.
Можно записать полную систему уравнений Навье-Стокса в векторной дивергентной форме:
,
(8)
– вектор состояния
потока.
Если
,
то
;
;
.
.
В уравнении (8) использовано расщепление по пространственным переменным (направлениям).
Расщепление по физическим переменным:
.
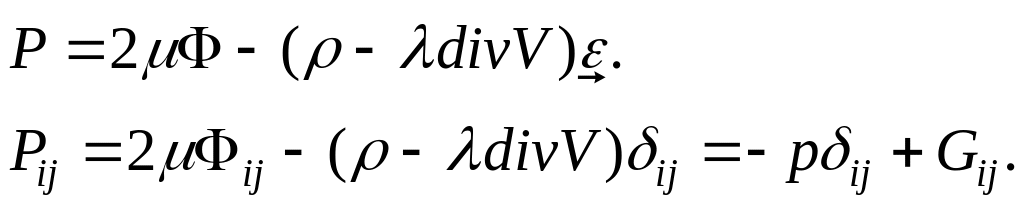
Можно выделить 3 различных физических процесса, в зависимости от действия гидродинамических сил, которые порождаются пространственными градиентами векторов гидродинамических потоков:
.
Тогда при расщеплении получим:
.
.
Конвективная матрица (матрица инерциальных сил).
.
Выпишем систему уравнений, в которой мы пренебрегаем силами, связанными с давлением и диссипативными эффектами. Вектор массовых сил:
.
.
Эта система описывает слабомолекулярное течение жидкости или газа и имеет гиперболический характер.
Рассмотрим первые четыре уравнения системы (уравнение неразрывности и три уравнения движения). Начнем с уравнений движения (2) – (4):
(*)
Из уравнения неразрывности (1) следует:
(**)
Из уравнений (*) – (**), получим:
.
Таким образом, скорость не зависит от времени.
2. Если в исходной системе (1) пренебречь силами, связанными с инерцией и диссипацией, а рассмотреть только действие сил, связанных с давлением, то получим:
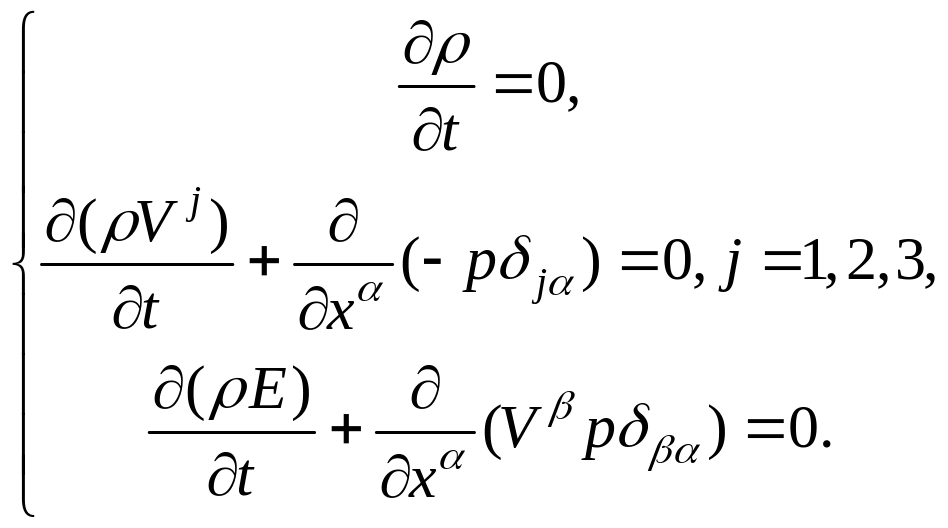
Видно, что плотность не зависит от времени, поэтому ее можно вынести за знак производной.
.
.
=>
.
.
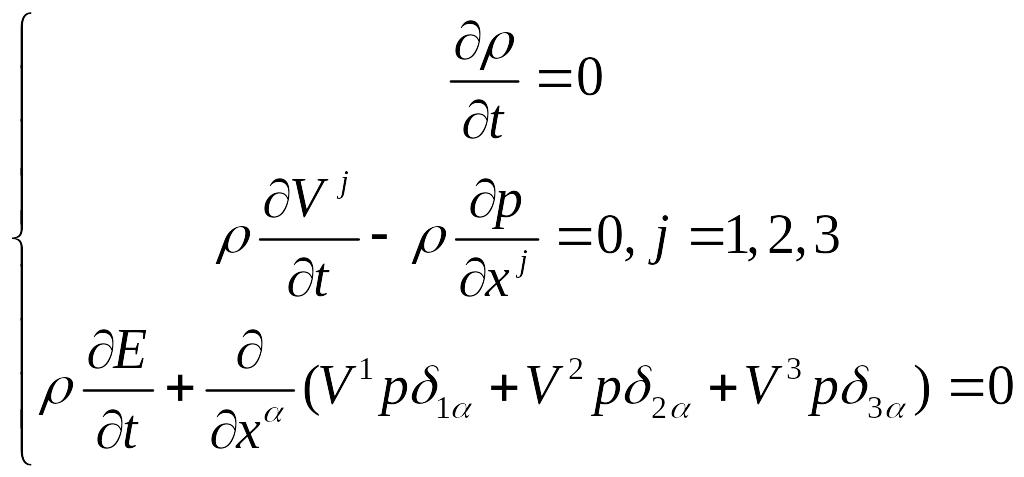
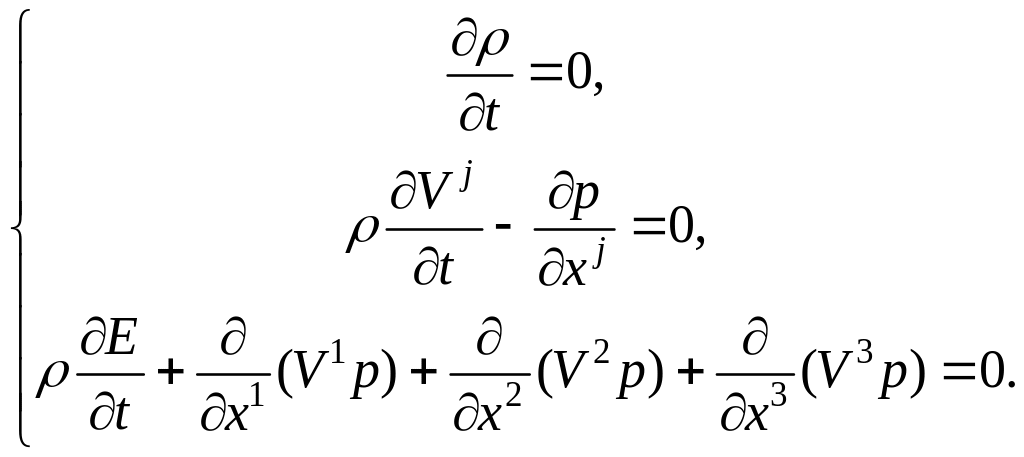
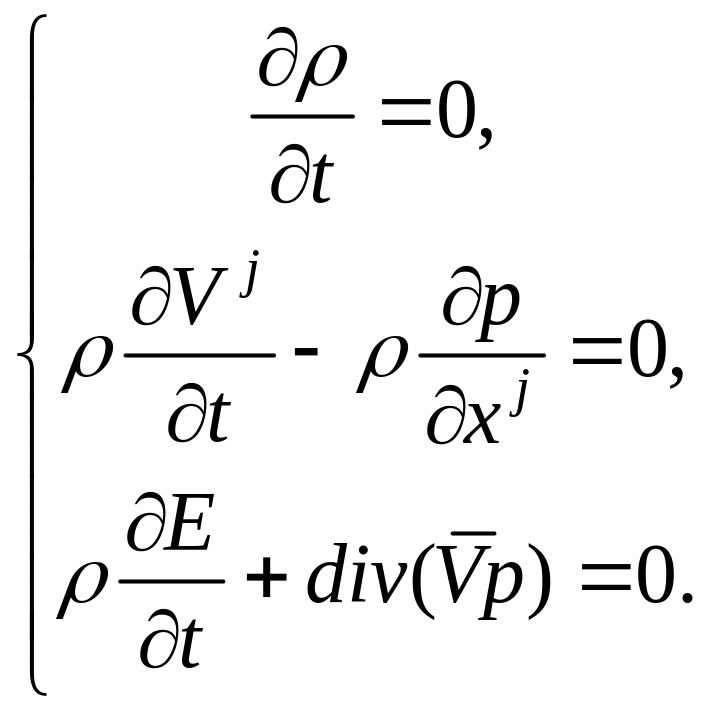
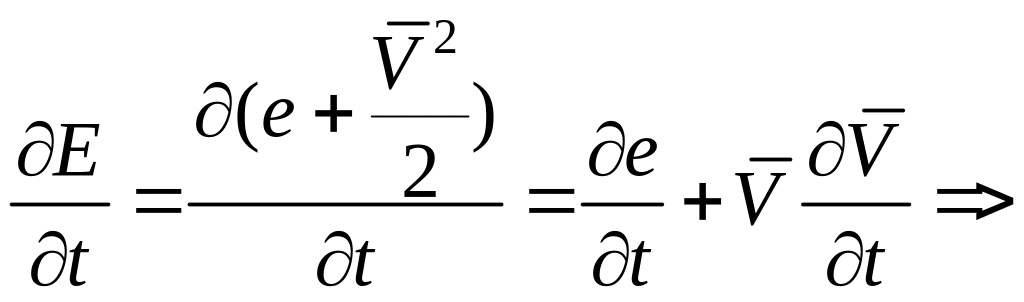
Воспользуемся
уравнением состояния
.
.
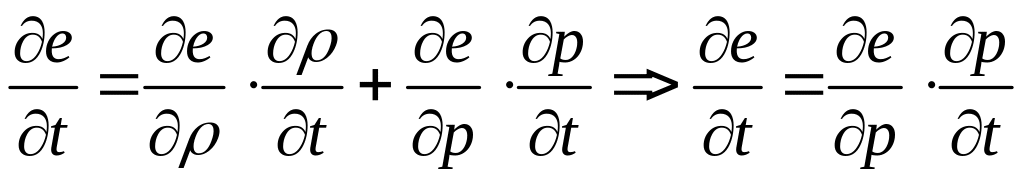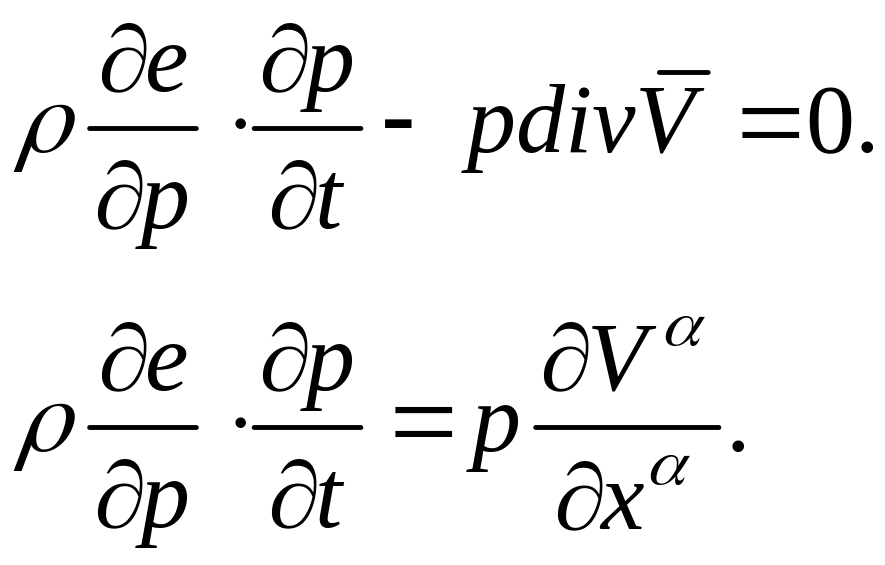
Выразим частные производные скорости по координатам через производную давления по времени:
.
Дифференциальным следствием этого уравнения будет уравнение
Из уравнения движения:
.
.
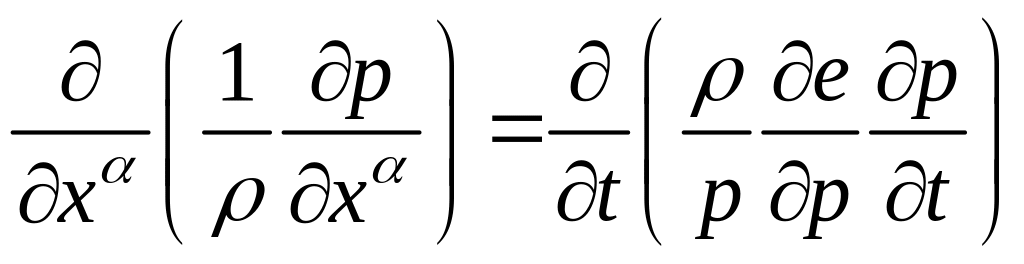Так как
и
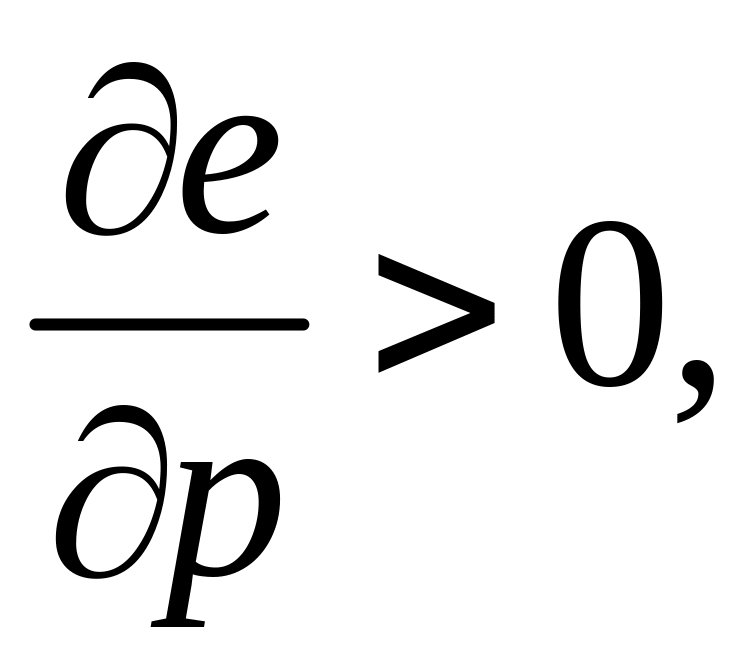полученное уравнение является уравнением
гиперболического типа. То есть в этом
случае система также носит гиперболический
характер.
3) Учитываются только силы диссипации
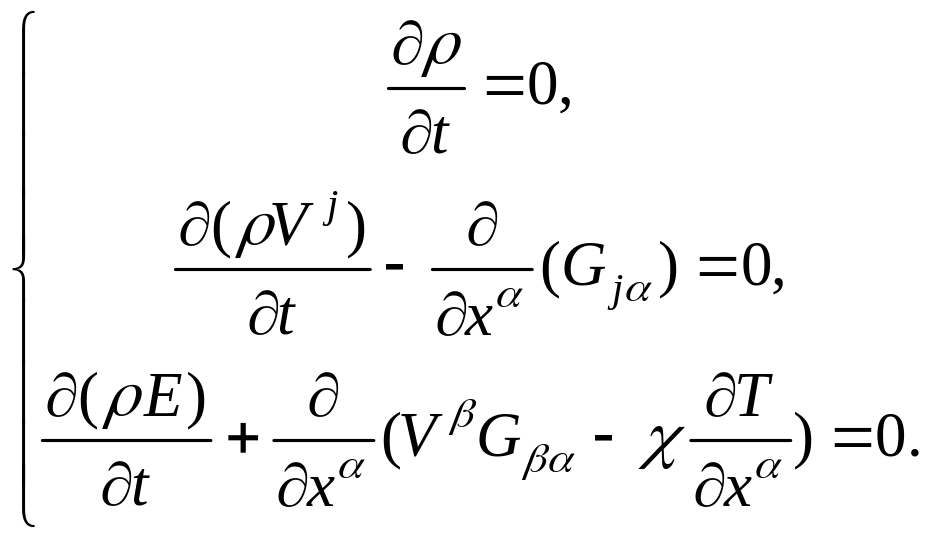
В этом случае, как
и в двух предыдущих,
.
После преобразований имеем:
Получили систему параболического типа (появляется вязкость).
Рассмотрены три простейших физических процесса. Для получения более сложных, будем рассматривать комбинации простейших процессов, например уравнения газовой динамики.