1.6.3. Свойства операторов разностных производных первого порядка

Рассмотрим разностную задачу, содержащую оператор левой разностной производной.

(1) ,

(2) .

Корректность задачи Коши для разностного уравнения I-го порядка.

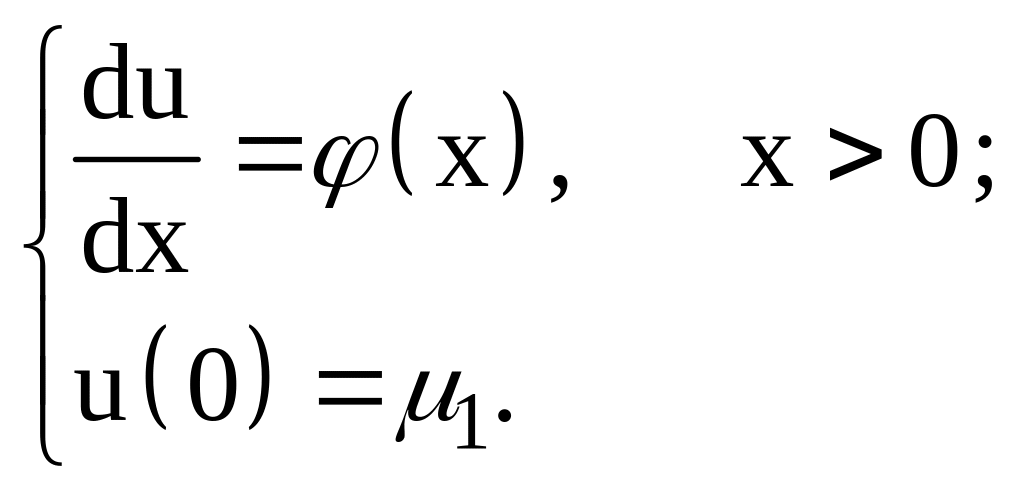
Выразим из (1)

,

, следовательно,

.

Так как , то можно взять максимум от всех .

, получаем:

.

Таким образом, задача (1), (2) устойчива по начальным данным и правой части.

Свойства оператора левой разностной производной.

(1) ,

(2) .

1. Задачу (1), (2) можно переформулировать таким образом, что:

(3)

4. 

Задачу (3), (4) перепишем в виде:

;

;

.

Для практических нужд полезно построить оператор сопряженный к .

Явное выражение этого оператора чрезвычайно важно.

Опр. 1

Оператор : , называется сопряженным к оператору , если выполняется следующее условие

Для этого рассмотрим скалярное произведение вида:

.

Таким образом, пришли к следующему равенству:

(5) .

Заметим, что - оператор правой разностной производной.

Введем оператор правой разностной производной:

(6)

Равенство (5) с учетом соотношения (6) означает, что для оператора левой разностной производной сопряженным является минус оператор правой разностной производной.

Итак,

(7) (8)

(9) .

Известно, что любой линейный оператор в гильбертовом пространстве сеточных функций можно представить в виде суммы его кососимметрической и самосопряженной частей, т.е.

(10) , (11) .

__________________________________________________________

‼ Показать, что если (11), то .

__________________________________________________________

Построим , привлекая в качестве оператора , оператор , задаваемый по формуле (7).

, следовательно,

(12)

.

Таким образом, мы получили признак кососимметричности оператора:

.

Поэтому оператор, задаваемый равенством (12), является кососимметрическим. Это означает:

(13) , а следовательно,

(14) .

Вернемся к соотношению (12). Из него следует, что оператор разностной производной второго порядка является кососимметрическим, если в граничных узлах он определен таким образом.

Возможна и другая интерпретация соотношения (12). Оператор А можно считать определенным на расширенной сетке , для которой , .

II. Покажем, что оператор является положительно определенным, точнее положительным, т.е. .

Для этого для любой сеточной функции необходимо доказать неравенство: .

Воспользуемся формулой (7).

что и требовалось доказать.

Кроме того, было получено соотношение:

(15) .

3. Каноническая форма двухслойных схем и ее применение к исследованию устойчивости

Необходимость введения двухслойных схем вызвана дискретизацией и исследованием эволюционных задач, которые можно записать в виде:

(1) ;

(2) , где .

- дифференциальный оператор.

(3) .

Для дискретизации задачи (1), (2) неудобно использовать выражение вида (3), т.к. переменная является выделенной в выражении (1), и аппроксимация будет, как минимум, двухточечного шаблона.

Так мы приходим к понятию двухслойной разностной схемы.

Каноническая форма.

Пусть Н конечномерное вещественное гильбертово пространство и .

Обозначим через и линейные операторы, переводящие .

Операторы и , например, это операторы разностных производных по пространственным переменным. В общем случае они могут зависеть от .

Пусть - векторный параметр, от которого зависят операторы и . Считаем, что фиксирован.

Рассмотрим абстрактную задачу Коши операторно-разностного типа.

(4) ;

(5) .

Можно считать, что задача (4), (5) будет дискретным аналогом задачи (1), (2), если выбрать операторы и подходящим образом: .

В уравнении (4) предполагается известными параметр , функция , заданными и функция .

Считаем, что операторы явно не зависят от . Также считаем, что оператор обратим, т.е. существует . Условие гарантирует обратимость оператора; , где - гильбертово пространство сеточных функций.

Рассмотрим теперь задачу (4), (5).

Опр. 1 Двухслойной схемы.

Поставленная выше операторно-разностная задача Коши (4), (5) называется двухслойной схемой, записанной в канонической форме.

Это семейство задач Коши зависящих от параметра .

Введем оператор перехода через все остальные функции, предполагая обратимость оператора В.

;

.

При достаточно малых значениях параметра можно определить оператор называемый оператором перехода.

Введем также обозначения:

; ; ;

; ; .

Тогда схему (4), (5) можно записать в виде:

(6) ;

(7) .

Определение корректности и устойчивости.

Для двухслойной схемы (6), (7) будем рассматривать множество решений, зависящих от как от параметра, а также от входных данных: начального условия и правой части .

Опр. 2

Говорят, что схема(6), (7) корректна (корректно поставлена), если для достаточно малых значений :

1. решение задачи (6), (7) существует и единственно;

2. для любых существуют , независящие от и , параметра , такие, что выполняется неравенство:

(8) .

Условие 2) является определением устойчивости (6), (7) по начальным данным и правой части.

Можно отдельно ввести условие устойчивости по начальным данным.

В приложениях возникает потребность получать более сильные по сравнению с (8) оценки устойчивости по начальным данным.

Опр. 3

Схема (6), (7) называется -устойчивой по начальным данным, если для любого n: выполняется неравенство:

(9) , где -константа независящая от ; .

Нетрудно видеть, что достаточным условием -устойчивости (9), является ограниченность оператора перехода S: .

Действительно, при однородной правой части имеем: .

(10) , если , то приходим к (9).

Замечание.

1. в определение -устойчивости, как правило, используются значения близкие к единице.

Например, ,

.

2. в определение корректности двухслойной схемы в условии устойчивости (8) часто используется несколько другая форма:

вместо (8) используют

(8′) .

Очевидно, что также является нормой, которую можно обозначить .

В соответствии с формой (8) и (8′), а также учтя отдельно начальные данные сформируем две задачи:

(12) ;

(13) ;

(14) ;

(15) .

Для этих задач должно выполняться:

(16) ;

(17) .

, а, следовательно, и

.

Оказывается, нет необходимости отдельно исследовать устойчивость по правой части, если схема -устойчива по начальным данным. Точнее имеет место теорема.

Теорема 1

(18) ;

(19) .

Если задача (18), (19) равномерно устойчива по начальным условиям ( -устойчива относительно начальных данных) в норме . Тогда она устойчива и по правой части и имеет место оценка:

,

где , .

Доказательство:

Выразим из (18) , предполагая, как и везде .

.

Очевидно неравенство:

(*) .

Решим вспомогательную задачу, оценив сверху норму оператора перехода.

Покажем, что , .

Заметим, что . Действительно, сформулируем вспомогательную задачу, отличающуюся от задачи (18), (19) однородной правой частью.

;

.

Из того, что схема (7), (8) - устойчива следует выполнение:

(20) ,

(21) , .

Возьмем норму от обеих частей равенства (20).

(22) .

Используем наименьшую норму оператора из его возможных норм.

Сравнивая (22) и (21), можем считать, что фигурирующее в определении (21) удовлетворяет неравенству.

Оценка (22) достигается в конечномерном случае при определенном выборе вектора .

Строго говоря, надо было указать .

В случае если и этого можно добиться выбором .

, то в роли функции , можно подставить собственную функцию оператора , которая соответствует собственному значению. Мы добьемся выполнения (22).

Вернемся к соотношению (*), где - постоянная, фигурирующая в определении - устойчивости.

,