Построение энергетической эквивалентности оператора второй разностной производной с переменными коэффициентами
До сих пор мы рассматривали простейшие операторы, не зависящие от пространственных переменных. На практике это редко встречающаяся ситуация. Поэтому получим оценки для оператора разностной производной второго порядка с переменными коэффициентами.
;
.
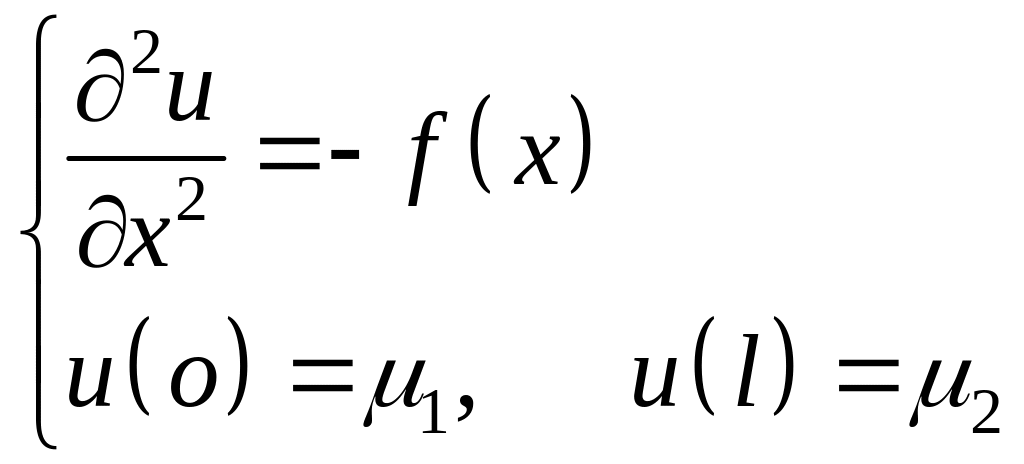
В двумерном случае рассматривается задача Дирихле.
;
,
В этих задачах мы приходим к оператору второго порядка с переменными коэффициентами.
(1) 
.
Будем использовать:
(2) 
.
Получим по возможности более точные оценки вида:
(3) 
,
где константы
и не могут быть улучшены.
Опр. 1
Постоянные
в неравенстве (3) называются постоянными
энергетической эквивалентности или
энергетическими постоянными.
Воспользуемся первой разностной формулой Грина для финитных сеточных функций.
(4) 
.
В соответствии с (4), скалярное произведение (2) запишется в виде:
(*)
.
В соотношении (1), если иметь в виду
аппроксимацию ОДУ II-го
порядка
.
Следовательно,
,
тогда:
(*)
Воспользуемся еще
раз формулой (4) в которой
,
прочитав ее справа на лево и умножив на
(-1).
.
Вспомним оценку
сверху для
,
т.е.
(5) 
,
тогда
.
Итак, получили оценку:
(6) 
.
Будем считать, что
- точная константа в (5).
___________________________________________________________
?? Можно
ли улучшить оценку (6), уменьшив
.
‼ Получить самостоятельно оценку снизу (7).
___________________________________________________________
(7) 
,
где
.
Приведем без вывода
соответствующие оценки – укажем
постоянные энергетической эквивалентности
для оператора
(двумерный
случай):
(8) 
(8) - дискретный аналог (9):
(9) 
; 
.
(10) 
,
где
(11) 
,
(12) 
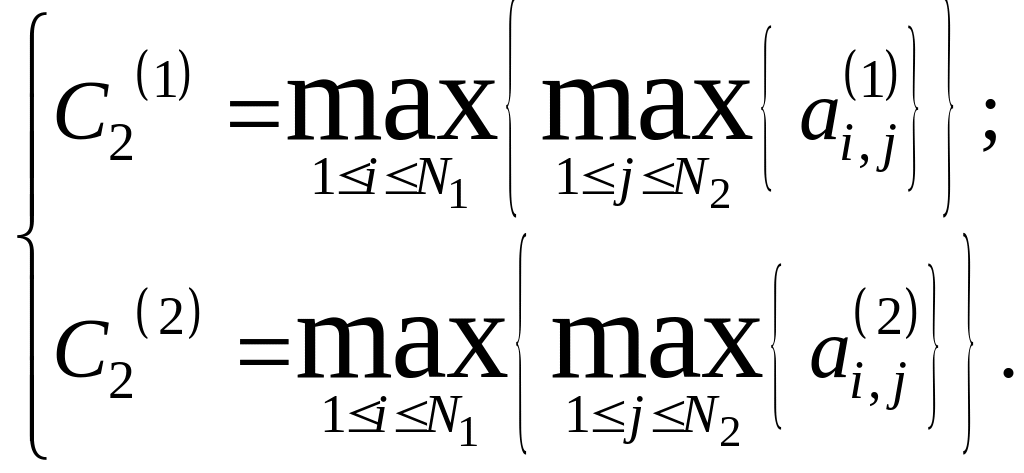
(13) 
,
где
(14) 
___________________________________________________________
‼ Получить самостоятельно оценки для: а) и ; б) уточнить формулы (12) и (13).
___________________________________________________________
Корректность операторно-разностных уравнений
1.7.1. Общие сведения
Построенные разностные аналоги краевой задачи для ОДУ II-го порядка, а также задачу Дирихле для уравнения Пуассона, могут быть представлены в виде операторного уравнения:
(1) 
.
Здесь
- известная функция правой части из
гильбертова пространства сеточных
функций,
- искомая сеточная функция, которая
может считаться финитной при
соответствующем переопределении
граничных условий и правой части.
,
,
,
.
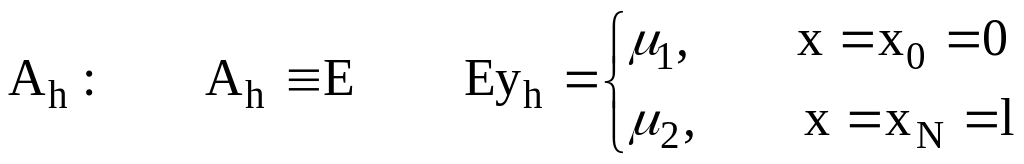
Пусть
нормы
и
- нормы, введенные на пространстве
функций, являющихся решением (1), норма
для
,
а норма
введена на пространстве функций,
являющихся правыми частями в (1), т.е.
для
.
В простейшем случае эти нормы могут совпадать.
Можно считать, что решение – это множество финитных функций.
Опр. 1
Операторное уравнение (1) называется корректным, если:
решение задачи (1) существует и единственно для всех
- семейство функций;для любой пары
существует
,
не зависящая от
,
такая, что выполняется неравенство:
(2) 
.
Гильбертово
пространство финитных функций обозначим
.
С пунктом 2) определения корректности, мы встречались ранее, называя его условием устойчивости по правой части. Новым здесь является то, что в левых и правых частях 2) могут фигурировать разные нормы, а также граничные условия, если они есть, учтены в правой части. Неравенство (2) означает, что малым изменениям входных данных соответствует малое изменение возмущений. Т.е. малое по норме изменение функции приводит к малому изменению нормы .
В
формулировке, как и ранее, подразумевается
линейность и ограниченность оператора
.
Докажем последнее утверждение, т.е., на ряду с задачей (1) рассмотрим задачу (3):
(3) 
.
Вычтем из (3) (1), получим
,
операторы задач (1), (3), (4) совпадают.
(4) 
.
.
Поскольку
,
то, следовательно,
.