Понятие о методе конечных элементов.
10. Общее описание метода.
1) Выполняется:
(1) 
,
- гильбертово пространство с введенным
в нем скалярным произведением.
Задача (1) формулируется в слабой (обобщенной) постановке.
(2) 
.
2) Строится
подпространство гильбертова пространства
и выбирается базис
в подпространстве. Базисные функции
должны быть такими, что
(3) 
Принципиальных препятствий нарушить условие (3) нет, однако в противном случае получаются системы линейных алгебраических уравнений с плотными матрицами, в противном случае матрицы разряженные, т.е. выполняется (3).
На
самом деле рассматривается семейство
подпространств
(последовательность
должна быть плотна в
.
3) Решение задачи (2) ищется приближенно в в виде линейной комбинации базисных функций.
(4) 
.
Для
поиска коэффициентов линейного
разложения
строится конечномерный аналог задачи
(2).
(5) 
.
4) Решение
задачи (5) после вычисления скалярных
произведений слева и справа сводится
к решению СЛАУ вида
.
5) После
нахождения
искомая функция
восстанавливается по формуле (4),
например, кусрчно-линейное восполнения
(4) и исследуется сходимость функции
к
при
,
т.е.
.
20. Пример построения и исследования конечно-элементой схемы.
Рассмотрим первую краевую задачу для ОДУ второго порядка.
(1) 
,
(2) 
.
Из курса дифференциальных уравнений известно понятие классического решения задачи (1), (2).
Нам
понадобятся пространства
,
каждое из которых рассматривается как
пополнение соответственно пространств
,
т.е.
или пространству
следует, что
,
т.е функции являются финитными.
,
.
Умножим
обе части уравнения (1) на функцию
и проинтегрируем по переменной
на отрезке
.
(3) 
Применим формулу интегрирования по частям.
(4) 
.
Учитывая равенство (4) получаем из равенства (3) следующее равенство
,
(5) 
.
Напомним определение обобщенного решения задачи (1), (2).
Опр.
Функция
,
такая, что для любой функции
выполняется равенство (5)называется
обобщенным или слабым решением задачи
(1), (2).
На отрезке построим в общем случае равномерную сетку
Для
построим базис из кусочно-линейных
функций, которые рассматривались ранее.
(6)
Элементами
пространства
являются все возможные линейные
комбинации функций вида (6), т.е.
кусочно-линеные функции, которые могут
изменять свои наклоны в узлах сетки_
,
и равны нулю на концах отрезка
.
Очевидно, квадраты базисных функций,
а также квадраты их производных
интегрируемы на отрезке
,
.
Выберем
функцию
и ее разложение по базису
(7) 
.
Также сформируем функцию , которую назовем далее приближенным значением задачи (5) и определенную следующим образом:
(8) 
,
где
.
Для
удобства считаем, что
.
Числа
,
которые как мы увидим дальше при
максимальном из шагов
,
будут стремиться к функции
,
т.е.
.
Ориентируясь на представление (7), (8) сформулируем обобщенную постановку дискретной задачи в .
Сформулируем понятие приближенного решения задачи (5).
Опр.
Функция
выполняется равенство
(9) 
.
Подставим
(7) и (8) в (9), считая, что
.
Поскольку
- произвольные, тогда будут произвольными
и
.
А значит последнее равенство выполняется,
тогда и только тогда, когда
,
-любое.
Зафиксируем значение индекса .
Если
,
то мы получаем тривиальное равенство.
Рассмотрим
случай, когда
,
получим:
(10) 
.
Разобьем
отрезок
на два:
и
.
,
.
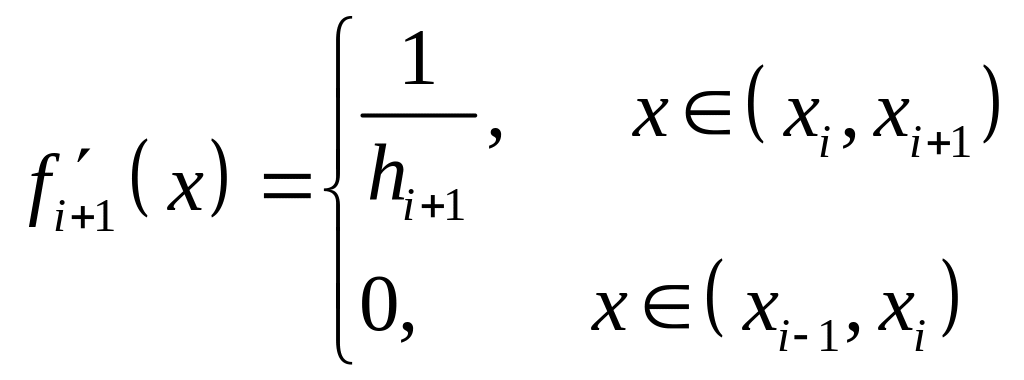
Используем
представления для интегралов
и
для преобразования (10). Введем следующие
обозначения:
; 
; 
; 
.
Итак, получаем СЛАУ:
___________________________________________________________________________________________________
‼ 1) Доказать, что матрица СЛАУ не вырожденная,
2) показать, что матрица СЛАУ является трех диагональной,
3) показать, что для нее применим метод прогонки, т.е. есть строгое диагональное преобладание.
___________________________________________________________________________________________________
Если выполняются пункты 1)-3), то решение задачи (5) существует и единственно и может быть найдено вычислением по устойчивому методу прогонки.
Коэффициенты
в явном виде вычислить не удается и на
практике используются квадратурные
формулы.
Реализация метода конечных элементов потребует применения некоторых теорем которые будут рассмотрены далее.
§3