Схемы переменных направлений
Эти схемы сочетают достоинства явных и неявных схем:
Абсолютно устойчивы, т.е. устойчивы при любых значениях шага по времени;
Являются экономичными схемами. Это означает, что затраты арифметических операций на получение значения функции
,
если все значения
известны, есть величина
арифметических
операций.
Рассмотрим смешанную задачу Коши для уравнения теплопроводности в прямоугольнике.
В области требуется найти решение уравнения:
(1) 
,
если заданы граничные условия:
(2) 
(3) 
.
Рассматриваем
случай, когда
.
Для
аппроксимации задачи (1), (2), область
покроем равномерной сеткой с шагами
по оси Ох и
по оси Оу .
,
,
.
Так как уравнение с постоянными коэффициентами, то будем использовать непосредственную аппроксимацию специального вида.
Введем вспомогательную сетку
.
Будем использовать так называемую схему Писмена – Рекфорда.
Схема Писмена – Рекфорда.
(4) 
,
(5) 
(6) 
,
(7) 
,
(8) 
.
Задача
(4) представляет собой систему трех
точечных уравнений относительно
функции
.
Если все
известны, то система (4) может быть решена
методом прогонки. Данный метод является
экономичным
операций. Прогонки выполняются вдоль
строк. Если все
найдены, то решая задачу (8) относительно
функции
,
задача которая также представляет
собой систему трех точечных уравнений,
заканчивая цикл вычислений к переходу
на
временной слой. Затраты на арифметические
операции составят
,
прогонки выполняются вдоль столбцов.
Тогда общее число операций составит
порядка
операций.
Исследуем
устойчивость схемы (6), (7) энергетическим
методом. Попутно установим вид функций
.
Запишем уравнения (4), (6) в операторном виде относительно пространственных переменных.
,
.
(4′) 
,
(6′) 
.
Операторы
в гильбертовом пространстве сеточных
функций определенных на сетке
и обращающихся в ноль в узлах
являются самосопряженными, и отрицательно
определенными, т.е.
.
Кроме
того, не трудно показать, что эти
операторы коммутативны, т.е.
.
Свойство
коммутативности выполняется только
для специальной геометрии области.
Область
должна быть односвязной областью
ступенчатой формы, границы которой
являются отрезками прямых параллельных
координатным осям. Также накладываются
ограничения на тип граничных условий.
Для граничных условий 3-го рода
коммутативность не выполняется.
Вычтем из (4) равенство (6).
,
выразим
(9) 
.
Последнее равенство позволяет нам определить вид функций .
Положим
в (9)
,
тогда
.
Примем во внимание граничное условие (2) исходной задачи.
(10) 
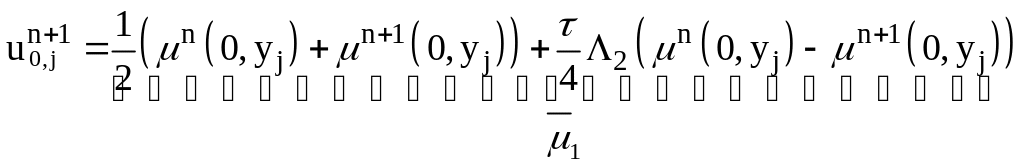
(11) 
.
Используя соотношения (4), (6) и (9), получим каноническую форму двухслойной схемы.
Сложим (4) и (6).
,
подставим (9) – выраженное ранее
.
,
,
.
Общий вид канонической формы:
.
Выполним очевидные преобразования.
,
.
Введем
оператор
,
,
,
.
Проверим операторное неравенство .
,
т.к.
,
то
.
Поскольку
и
,
то
неравенство выполняется. Следовательно,
схема параллельных направлений устойчива
в энергетическом пространстве
,
где
.
Замечание.
В
явном виде нигде не использовалась
коммутативность операторов
,
а только положительноопределенность
оператора
,
однако это можно требовать при выполнении
коммутативности этих операторов.
Лемма.
Пусть
произвольный вектор из
,
- некоторые действительные числа.
Тогда
для выполнения неравенства
необходимо и достаточно чтобы все
.