1.4.2. Консервативные и не консервативные разностные схемы

Как было показано ранее, дискретные модели должны, по возможности, удовлетворять основным балансовым соотношениям (разностным законам сохранения) которым удовлетворяют непрерывные модели.

Рассмотрим уравнение (1) из параграфа 1.4.1 и еще раз проинтегрируем его по на отрезке т.е.

Получаем:

. (1)

Физический смысл левой и правой частей полученного равенства (1) следующий: слева стоит разность потоков тепла, втекающих через левый и правый концы стержня, а справа – тепло, которое поступило за счет собственного тепловыделения, например, химической реакции, и внешних тепловых источников.

Если - сток, а - источник тепла.

Не трудно получить разностный аналог балансового соотношения для уравнения (1).

Возьмем разностное уравнение (13) из параграфа 1.4.1.

.

домножим на и просуммируем полученное разностное соотношение по , тогда выражение в скобках упрощается:

и в итоге получим:

. (2)

Очевидно, что (2) есть разностный аналог (1) и баланс на дискретном уровне выполняется. Дискретные модели, которые удовлетворяют балансовым соотношениям, называются консервативными.

Заметим, что исходное уравнение (1) из предыдущего параграфа имело дивергентный вид (первое слагаемое стоит под знаком производной).

Рассмотрим пример дискретной модели, которая не удовлетворяет балансовому соотношению.

Запишем уравнение: в не дивергентном виде. Дифференцируя произведение, получаем:

. (1')

Аппроксимацию будем выполнять на внутренних узлах равномерной сетки

.

В узле номера разностное соотношение запишем в виде (используя второй порядок аппроксимации разностных производных) :

. (3)

Наибольшие изменения претерпели первые два слагаемых.

Докажем вспомогательное утверждение.

. (5)

Здесь , тогда ( ) ;

и

. (4)

Для простоты вывода формулы (5) будем считать, что здесь

, (6)

которое отличается от

из раздела 1.4.1 тем, что

.

Считая, что все функции в уравнении обладают необходимой степенью гладкости получаем:

,

что и требовалось доказать в (5).

Используя соотношение (3) и (5) , получаем:

.

Просуммируем последние уравнение предварительно умножив его обе части на . Суммирование производим по . Тогда

.

Сравнивая полученное выражение с балансным соотношением (2), заметим, что появился посторонний член вида

,

который отвечает за дисбаланс.

1.4.3. Исследование аппроксимации дифференциального уравнения

Покажем, что построенная интегро-итерполяционным методом разностная схема (при определенных условиях) аппроксимирует исходное дифференциальное уравнение со вторым порядком точности.

Определение. Пусть достаточно гладкая функция, определенная на отрезке , на котором построена сетка . Говорят, что разностный оператор аппроксимирует дифференциальный оператор L в узле сетки с порядком m, если выполняется равенство:

.

Вначале получим вспомогательный результат – достаточное условие второго порядка аппроксимации дифференциального выражения:

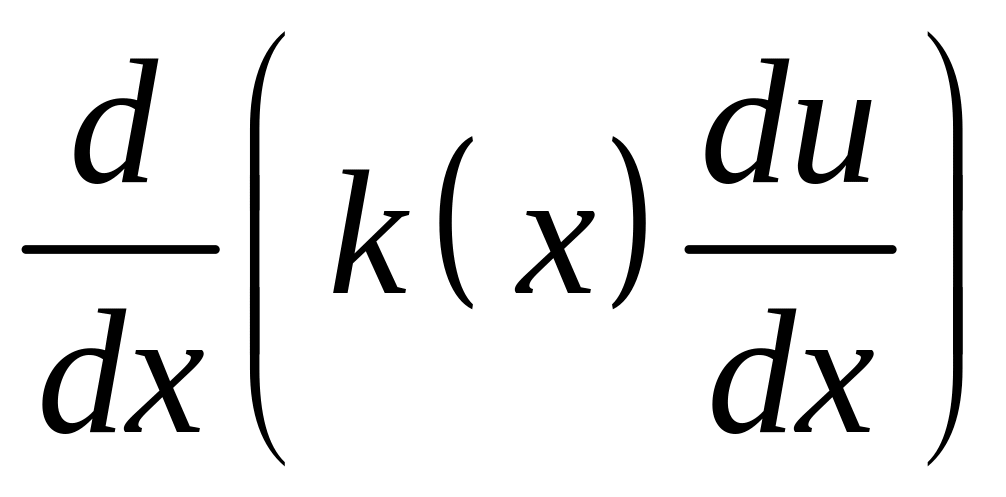
в узле равномерной сетки .

Рассмотрим погрешность аппроксимации:

.

Для того, чтобы погрешность аппроксимации имела второй порядок точности достаточно выполнения следующих условий:

(1)

Вспомним, что имеет место равенство:

. (2)

. (3)

Рассмотрим выражение с подставленными в него формулами (2) и (3).

.

. (4)

С учетом последнего равенства (4) получаем:

. (4′)

Рассмотрим разность вида:

Воспользуемся достаточным условием (1)

.

Достаточное условие (1) будем использовать для оценки погрешности аппроксимации дифференциального уравнения:

Введем для удобства функцию , .

, .

В силу формулы центральных прямоугольников для численного интегрирования

. (5)

Введем функцию ; .

.

.

,

то есть

. (6)

Подставим (6) в (5).

. (7)

Аналогично получаем для :

. (8)

Перейдем к проверке достаточных условий.

Заметим, что (7) и (8) означают:

исправ (9)

Тогда

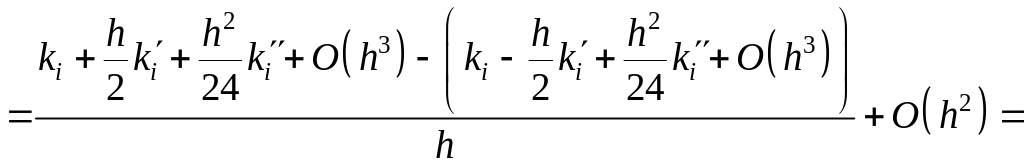
. Выполнено первое условие.

– второе условие также имеет место.

При необходимой гладкости функций , оценка \

имеет место.

Нетрудно видеть (надо воспользоваться квадратурными формулами), что

, (10)

. (11)

,

.

Соберем полученные результаты воедино.

. (12)

Сложим соотношения (11) и (12) и вычтем (10) умноженное на .

.

- разностное выражение, - дифференциальное выражение.

Таким образом, получено, что разностное выражение заменяет (аппроксимирует) непрерывное выражение с погрешностью .

Из определения следует, что построено разностное выражение, оператор которого аппроксимирует исходный оператор со вторым порядком.