1.4.9. Исследование устойчивости разностных задач методом гармоник

Метод гармоник позволяет получить необходимое условие устойчивости дискретной модели, отсеивая заведомо непригодные схемы. Он не учитывает влияние граничных условий и правых частей на решение задачи. Таким образом, этот метод дает необходимое условие устойчивости по начальным условиям.

Рассмотрим задачу:

(1)

. (2)

. (3)

Будем искать решение в виде:

, (4)

где - мнимая единица, - номер узла по пространству.

.

Если , то схема не устойчива, т.е. не существует универсальной константы М которую можно подставить в неравенство:

,

т.е. при .

Подставим (4) в (1), получим:

,

т.к. ,

то получаем:

;

, .

Очевидно, что

,

так как .

,

тогда .

Таким образом, получили

.

Это очень жесткое ограничение для разностных схем.

Проблема не в большом количестве шагов, а в том, что при числе шагов десятков тысяч погрешность накапливается и может поглотить решение.

1.4.10. Неявная схема для уравнения теплопроводности

Рассмотрим задачу для уравнения теплопроводности с постоянными коэффициентами.

. (1)

. (2)

. (3)

Согласование начальных и граничных условий:

.

Поставим в соответствие задачи (1), (2), (3) неявную схему (4), (5), (6).

Неявная схема.

(4)

. (5)

. (6)

Система (4) представляет собой систему линейных алгебраических уравнений с трех диагональной матрицей; главная диагональ имеет вид: . Матрица симметрична и обладает свойством строго диагонального преобладания.

Граничные условия (6) могут быть учтены в векторе правых частей.

.

Правая часть будет иметь вид:

.

Поскольку матрица А имеет строго диагональное преобладание, то задача (4-6) однозначно разрешима.

Погрешность аппроксимации задачи (4-6) на решении задачи (1-3) будет исследована ниже в случае схемы с весами.

Исследуем устойчивость построенной схемы методом гармоник.

Как и ранее будем искать решение задачи (4-6) с нулевыми граничными условиями и нулевой правой частью в виде:

. (7)

Подставим (7) в (4):

,

,

так как ,

то получаем:

.

.

Очевидно, что

.

Сравним полученные результаты для явной и неявной схем.

Явная схема устойчива, если , неявная схема устойчива для любых шагов по времени и по пространству.

1.4.11. Схема с весами

Рассмотрим задачу для уравнения теплопроводности с постоянными коэффициентами.

. (1)

. (2)

. (3)

Согласование начальных и граничных условий:

.

Для уравнения теплопроводности схема с весами имеет вид:

. (4)

- числовой параметр:

. (5)

. (6)

Согласование начальных и граничных условий:

. (7)

Получим задачу для погрешности решения.

Подставим

в (4, 5, 6).

. (8)

. (9)

. (10)

Задача (8-10) поставлена.

Задача (8) по своей структуре (по результату действия оператора левой части уравнения) аналогична задаче (4), если (4) переписать в виде:

. (4′)

Отличия возникли в правых частях у задачи (4′) это , у (8) – погрешность аппроксимации разностных уравнений (4) на решении непрерывной задачи (1, 2, 3).

Исследуем эту погрешность аппроксимации, предполагая, что разностная схема (4, 5, 6) устойчива.

______________________________________________________________

‼ Исследовать условия устойчивости для задачи (4 - 6) методом гармоник.

______________________________________________________________

Исследуем погрешность аппроксимации.

. (11)

.

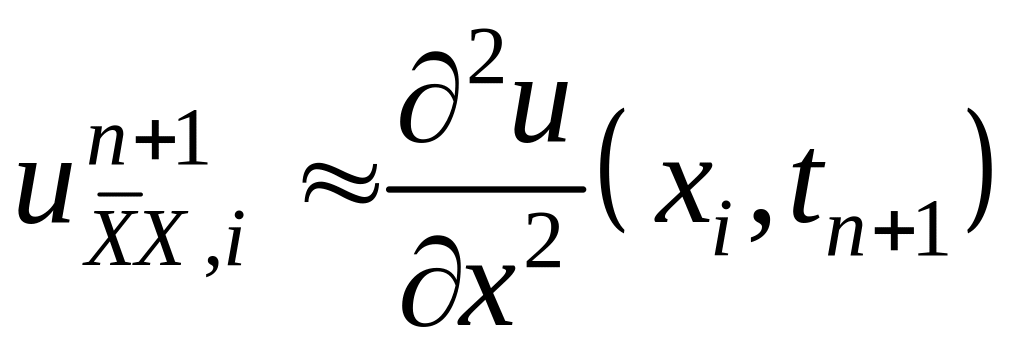
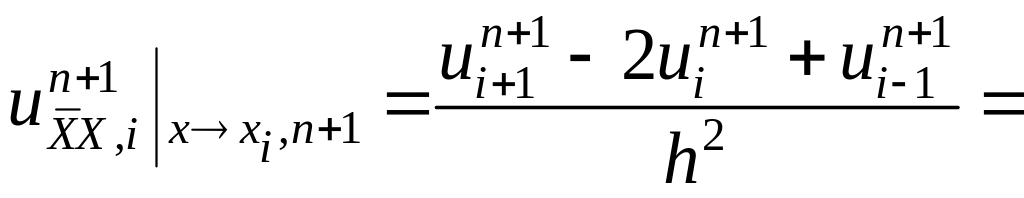
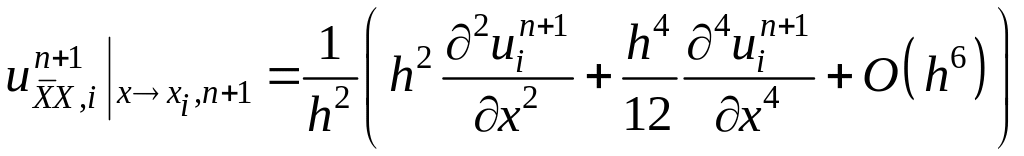. (12)

Аналогично:

. (13)

Подставим (12), (13) в (11).

. (14)

Разложим функции, стоящие в фигурных скобках по переменной в окрестности в ряд.

. (15)

. (16)

. (17)

. (18)

.

. (19)

Подставим (15)-(19) в (14).

.

Пусть ;

.

. (20)

Из полученного представления видно, что при погрешность аппроксимации

.

В частности, если , то - симметричная схема с весами.

Если имеем явную схему, для которой

.

Если имеем неявную схему, для которой .

Воспользуемся следующим равенством:

. (21)

(22)

подставим (22) в (20):

.

Преобразуя выражение получаем:

.

Будем считать, что

.

(23)

Выберем итерационный параметр так, чтобы первое слагаемое обращалось в ноль.

.

Следовательно,

.

При таком итерационном параметре мы имеем схему повышенного порядка аппроксимации.

______________________________________________________________

‼ Существуют ли такие значения итерационного параметра , при которых погрешность аппроксимации ?

______________________________________________________________

Были рассмотрены двухслойные разностные схемы. Для уравнений гиперболического типа используют трехслойные разностные схемы.