1.4.6. Разностные операторы и их свойства

1. Разностные тождества

1.1. Формулы разностного дифференцирования произведения

Известна непрерывная формула дифференцирования произведения: .

Она имеет следующий разностный аналог:

. (1)

. (2)

Выведем формулу (1).

.

Выведем формулу (2).

.

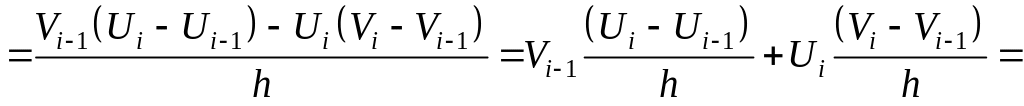
Формулы суммирования по частям.

.

Далее удобно ввести обозначения трех типов скалярных произведений сеточных функций.

; ; . (3)

______________________________________________________________

‼ Проверить аксиомы скалярного произведения самостоятельно.

______________________________________________________________

На сетке строится разностная схема:

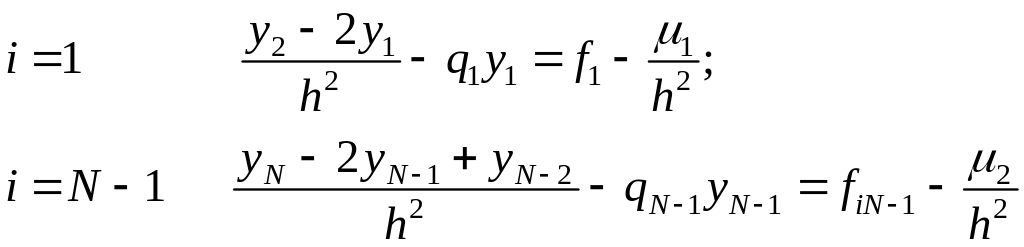
Таким образом, получим:

Если граничные условия 2-го и 3-го рода, то введение граничных условий 1-го рода сопровождается изменением самого оператора.

. (3)

. (4)

Докажем, например, формулу (3′).

Воспользуемся формулой:

.

.

__________________________________________________________________

‼ Доказать формулу (4) самостоятельно.

__________________________________________________________________

1.2. Первая разностная формула Грина

- непрерывный аналог.

. (5)

Пусть в формуле (3′) , тогда получаем (5).

.

Частный случай формулы Грина, когда

.

(6)

1.3. Вторая разностная формула Грина

Непрерывный аналог этой формулы:

.

Эту формулу легко получить базируясь на формуле (5) – первой формуле Грина.

. (7)

В соответствии с формулой (5) имеем, заменив ,

. (8)

Из (5) вычтем (8).

так как .

Из формулы (7) следует, что оператор является самосопряженным в пространстве сеточных функций, определенных на сетке и обращающихся в ноль в узлах , т.к. все выражения в круглых скобках в правой части (7) обращаются в ноль, откуда

.

2. Оператор разностной производной второго порядка и его собственные значения

Далее будем рассматривать оператор второй разностной производной вида: .

Этот оператор является положительно определенным в пространстве , то есть для любой функции выполняется неравенство

.

Значит, существует обратный оператор и уравнение однозначно разрешено. Этот факт следует из соотношения (6). Положим в формуле (6) , тогда имеем

.

Следовательно, что и требовалось доказать.

Рассмотрим классическую задачу на собственные значения для ОДУ II-го порядка вида:

. (1)

. (2)

Нужно найти и , которые удовлетворяют уравнению.

Сделаем предположение о том, что . Иначе среди вещественных функций не найдется таких, которые удовлетворяют условию (2).

При , любое.

.

.

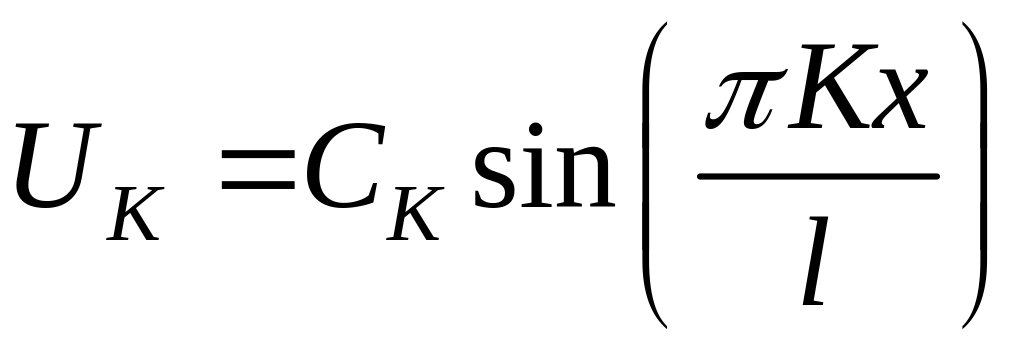Проведем нормировку:

.

, иначе .

Разностный аналог задачи (1), (2) имеет вид:

. (3)

. (4)

Будем искать решение задачи (3), (4) в виде: .

.

. (5)

. (6)

. (7)

. (8)

(9)

. (9′)

Потребуем, чтобы удовлетворялись граничные условия (4), если

.

.

. (10)

Подставим (10) в (9′), получим

.

Собственные функции, с точностью до коэффициента, для дискретной задачи с учетом нормировки совпадают с собственными функциями непрерывной задачи. Собственные значения - иные, нетрудно видеть, что они меньше собственных чисел непрерывной задачи. Даже для К=1 собственные значения дискретной задачи меньше собственных значений непрерывной задачи

.

Собственные функции дискретной задачи после нормировки совпадают с собственными функциями непрерывной задачи и имеют вид:

.

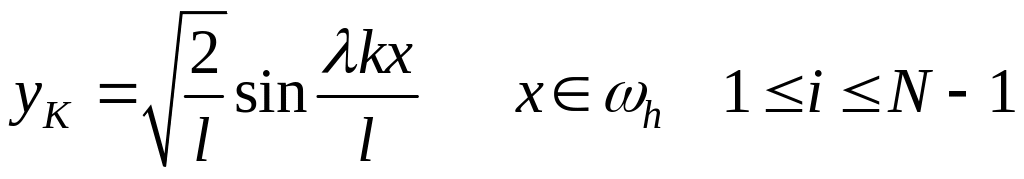Если устремить шаг к нулю, мы получим неопределенность: .

Возьмем к=1 – наименьшее собственное значение:

.

Найдем оценку для наибольшего собственного значения дискретной задачи, соответствующего к=N-1:

.

Для простоты считаем, что , тогда имеем следующий результат: .

______________________________________________________________

‼ Показать самостоятельно, что . Найти наибольшую

______________________________________________________________