Розрахунки характеристик положення варіаційного ряду.

Для визначення середньої арифметичної скористаємося сумою даних, обчислених в графі 3 табл.: ,

а також об'єм сукупності =31. По формулі знаходимо .

У даному варіаційному ряду мода як варіант, що має найбільшу частоту, Мо = 1,32с, Ме = 1,32с.

Враховуючи малу відмінність між середньою арифметичною = 1,34с, медіаною Ме = 1,32 і модою Мо = 1,32с, можна зробити висновок про однорідність початкових величин.

Лабораторна робота 11 «Порівняльний аналіз даних в спорті за параметричними критеріями»

1. Параметричний критерій Ст’юдента.

2. Параметричний критерій Фішера

Література:

1. Ашанин В.С. и др. Применение электронных таблиц для статистической обработки данных (на примере Microsoft Ехсеl). Серия “Спортивная информатика”, Вып. 1 - Харьков: ХаГИФК, 1997 - 66 с.

2. Дюк В.А. Обработка данных на ПК в примерах. - СПб.: Питер, 1997-240 с.

3. Толбатов Ю.А. Загальна теорія статистики засобами EXCEL. Навчальний посібник. – К.: Четверта хвиля, 1999.-224 с.

4. Начинская С.В. Основы спортивной статистики. - К.: Вища школа, 1987. – 189 с

Хід роботи:

Теоретичний матеріал Параметричний критерій Ст’юдента

Критерій Ст’юдента використовується як параметричний для дослідження рівновеликих вибірок. Відповідність нормальному закону розподілу обов'язкова. Критерій застосовується у разі порівняння вибірок по абсолютних значеннях їх середніх арифметичних. У практиці спорту він придатний для порівняння груп про значенню їх середніх показників.

,

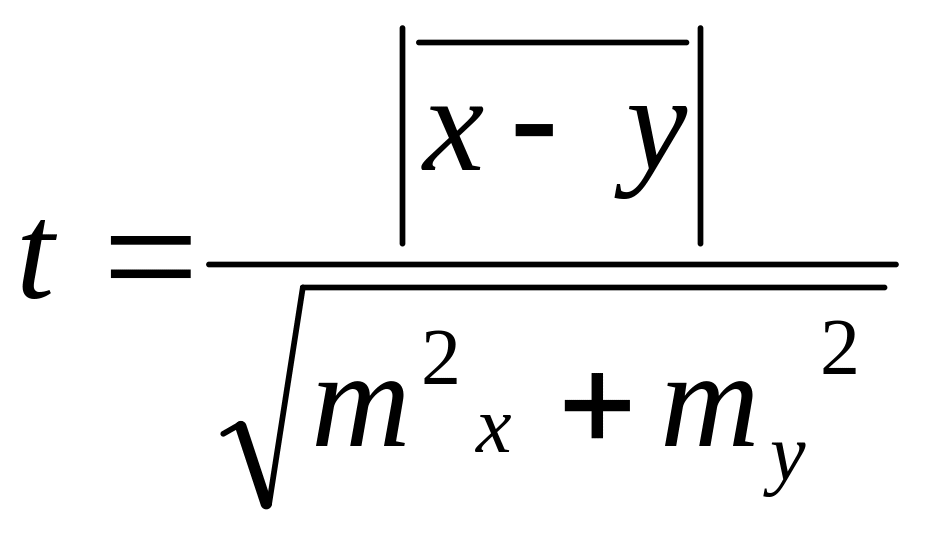де , - середні арифметичні порівнюваних груп; m₁,m₂ – помилки репрезентативності порівнюваних груп.

При вибраній надійності P для досліджуваного об'єму вибірки (n₁+n₂-2) відповідно до таблиці Ст’юдента знаходимо граничне значення критерію t_гр. Достовірність відмінності порівнюваних груп визначається при зіставленні обох критеріїв: t ≥ tгр - відмінність достовірна; t ≤ tгр - відмінність недостовірна.

Критерій Стьюдента дозволяє оцінювати вибірки на стабільність показників; достовірність та відмінність показників.

Параметричний критерій Фішера

Даний критерій застосовується як параметричний для порівняння різновеликих малих і середніх вибірок. Дотримання нормального закону розподілу необов'язкове. За допомогою критерію Фішера можна порівняти дисперсії вибірок. Таким чином, критерій застосовується у разі порівняння груп по чиннику розсіювання, тобто оцінюється порівняльна характеристика груп на стабільність. Визначається критерій Фішера по формулі

,

де D₁, D₂ – дисперсії порівнюваних вибірок. При цьому D₁>D₂.

При заданій надійності P і об'ємах порівнюваних вибірок n₁=19 і n₂=17 з таблиці Фішера знаходимо граничне значення критерію F_гр. При порівнянні критеріїв визначаємо достовірність відмінності вибіркових середніх: якщо F ≥ F_гр – достовірно; якщо F < F_гр – недостовірно.

Практична частина

Вправа 1. Порівняти показники Гарвардського степ-тесту юних спортсменів 11 – 12 років (х_і) та 13 -14 років (у_і) та зробити висновок про динаміку їхньої працездатності.

Рішення. Знайдемо основні характеристики варіаційного ряду 1 групи спортсменів 11 – 12 років (х_і):

хі	ni	xi*ni
85	2	170	-6	36	72
88	3	264	-3	9	27
90	7	630	-1	1	7
93	4	372	2	4	16
95	3	285	4	16	48
98	1	98	7	49	49
	20	1819			219

1. Для визначення середньої арифметичної скористаємося сумою даних, обчислених в графі 3 табл.= 1819:

,

а також об'єм сукупності =20. По формулі знаходимо

.

2. У даному варіаційному ряду мода як варіант, що має найбільшу частоту представлена: Мо = 90

3. Значенню медіани відповідає значення х, яке знаходиться на серединній позиції варіаційного ряду з індексом k за формулою:

На позиції k = 10,5 знаходиться значення х = 90, отже Ме = 90

4. Дисперсія знаходиться за формулою:

5. Середнє квадратичне відхилення:

6. Коефіцієнт варіації:

7. Похибка репрезентативності вказує наскільки вибірка відповідає генеральній сукупності та знаходиться за формулою:

Знайдемо основні характеристики варіаційного ряду 2 групи спортсменів 13 – 14 років (у_і):

уі	ni	уi*ni
95	2	190	-6	36	72
99	4	396	-2	4	16
100	5	500	-1	1	5
103	6	618	2	4	24
105	2	210	4	16	32
108	1	108	7	49	49
	20	2022			198

1. Для визначення середньої арифметичної скористаємося сумою даних, обчислених в графі 3 табл.= 2022:

,

а також об'єм сукупності =20. По формулі знаходимо

.

2. У даному варіаційному ряду мода як варіант, що має найбільшу частоту представлена: Мо = 103

3. Дисперсія знаходиться за формулою:

4. Середнє квадратичне відхилення:

5. Коефіцієнт варіації:

7. Похибка репрезентативності вказує наскільки вибірка відповідає генеральній сукупності та знаходиться за формулою:

Висновок. Порівнюючи показники працездатності двох груп юних спортсменів за допомогою критерію Ст’юдента, оцінюємо середні значення:

При надійності Р = 0,95 та об’ємах вибірок n₁ + n₂ – 2 = 20 + 20 – 2 = 38 з таблиці Ст’юдента знаходимо t_гр = 2,02.

Так як t > t_гр, приходимо до висновку, що різниця між порівнюваними групами статистично достовірна. Це значить, що показники Гарвардського степ – тесту у юних спортсменів 13 – 14 років відрізняються від аналогічних показників спортсменів 11 – 12 років. Таким чином, в досліджуваному віці спортсменів спостерігається значне збільшення працездатності.

Вправа 2. Поглинання кисню, л/мін, зміряне під час тривалої роботи на витривалість у двох груп спортсменів xi і yi. Визначити, чи принципова відмінність між цими групами по стабільності поглинання кисню.

Рішення. Знайдемо основні характеристики варіаційного ряду 1 групи (х_і).

xi	ni	xi*ni	xi-x	(xi-x)^2	(xi-x)^2*ni
4.0	7	28.0	-0.3	0.09	0.63
4.1	9	36.9	-0.2	0.04	0.36
4.2	8	33.6	-0.1	0.01	0.08
4.4	10	44.0	0.1	0.01	0.10
4.6	4	18.4	0.3	0.09	0.36
4.7	3	14.1	0.4	0.16	0.48
	41	175.0			2.01

1. Для визначення середньої арифметичної скористаємося сумою даних, обчислених в графі 3 табл.= 175,0: ,

а також об'єм сукупності =41. По формулі знаходимо .

2. У даному варіаційному ряду мода як варіант, що має найбільшу частоту представлена: Мо = 4,4

3. Значенню медіани відповідає значення х, яке знаходиться на серединній позиції варіаційного ряду з індексом k за формулою:

На позиції k = 21 знаходиться значення х = 4,2, отже Ме = 4,2

4. Дисперсія знаходиться за формулою:

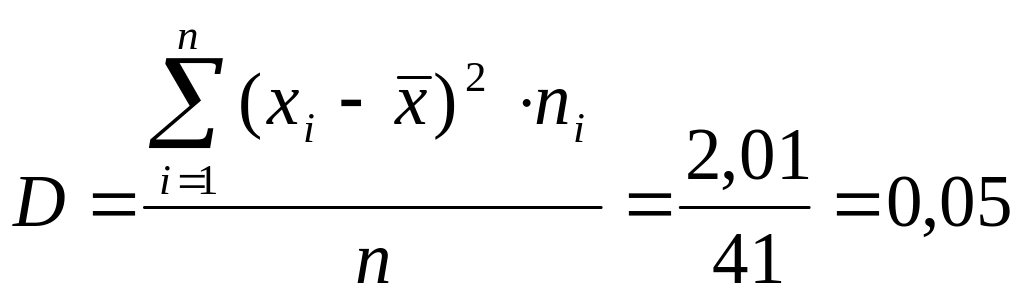
5. Середнє квадратичне відхилення:

6. Коефіцієнт варіації:

Знайдемо основні характеристики варіаційного ряду 2 групи (у_і):

уі	ni	yi*ni	yi-y	(yi-y)^2	(yi-y)^2*ni
4.0	2	8.0	-0.4	0.16	0.32
4.3	4	17.2	-0.1	0.01	0.04
4.5	9	40.5	0.1	0.01	0.09
4.6	3	13.5	0.2	0.04	0.12
4.7	1	4.7	0.3	0.09	0.09
	19	83.9			0.66

1. Для визначення середньої арифметичної скористаємося сумою даних, обчислених в графі 3 табл.= 83,9:

,

а також об'єм сукупності =19. По формулі знаходимо

.

2. У даному варіаційному ряду мода як варіант, що має найбільшу частоту представлена: Мо = 4,5

3. Дисперсія знаходиться за формулою:

4. Середнє квадратичне відхилення:

5. Коефіцієнт варіації:

Висновок. Знаходимо значення критерію Фішера за формулою

При надійності Р =0,95, об'ємах вибірок n₁=41 і n₂=19 граничне значення критерію F_гр = 2,0. Оскільки 1,7 < 2,0 (F < F_гр), відмінності між групами статистично недостовірно, тобто групи різні неістотно.