Методи знаходження ймовірностей.

Існують різні методи визначення вірогідності як чисельної міри ступеня об'єктивної можливості події. Перш за все розглянемо так зване частотне визначення.

Припустимо, що було проведено N випробувань і в результаті досліджувана випадкова подія А з'явилося n раз. Число і прийнято називати частотою події А, а відношення числа випробувань n, при яких подія А відбулося, до загального числа виконаних дослідів (випробувань) N є відносною частотою події А.

При невеликому числі дослідів відносна частота події носить значною мірою випадковий характер і може помітно змінюватися від однієї групи дослідів до іншої. Проте при збільшенні числа дослідів відносна частота події поступово втрачає свій випадковий характер. Випадкові обставини, супроводжуючі кожен окремий досвід, в масі дослідів взаємно погашаються, і частота поступово стабілізується біля деякої постійної величини. Це властивість стійкості частот при великому числі однорідних дослідів - одна з найхарактерніших закономірностей, спостережуваних в масових випадкових явищах.

Як ілюстрація розглянемо кидання монети. Існують два можливі результати - “орел” і “решка”. Визначимо експериментальним шляхом відносну частоту появи “решки”. Для цього кинемо монету 10, 100 і т.д раз і запишемо результати випробування в таблицю.

Таблиця 14.

Результати дослідження ймовірності випадіння двох подій

Число кидків	Число		Відносна частота
	орлів	Решок
10 100 1000 10000	7 39 565 4968	3 61 445 5032	0,3 0,61 0,445 0,5032

Результати показують, що відносна частота випадання “решки” із збільшенням дослідів прагнути до 0,5. Знаменитий статистик К.Пірсон кидав монету 24000 разів і одержав при цьому 11988 “решок”, що дає відносну частоту 0,4995, надзвичайно близьку до 0,5.

Стійке значення відносної частоти можна прийняти як об'єктивну числову міру ступеня можливості появи події А (тобто вірогідність). Позначимо це значення через Р (А). Розглянемо математичне слідство такого частотного визначення вірогідності. Використовуючи поняття межі, визначимо вірогідність як

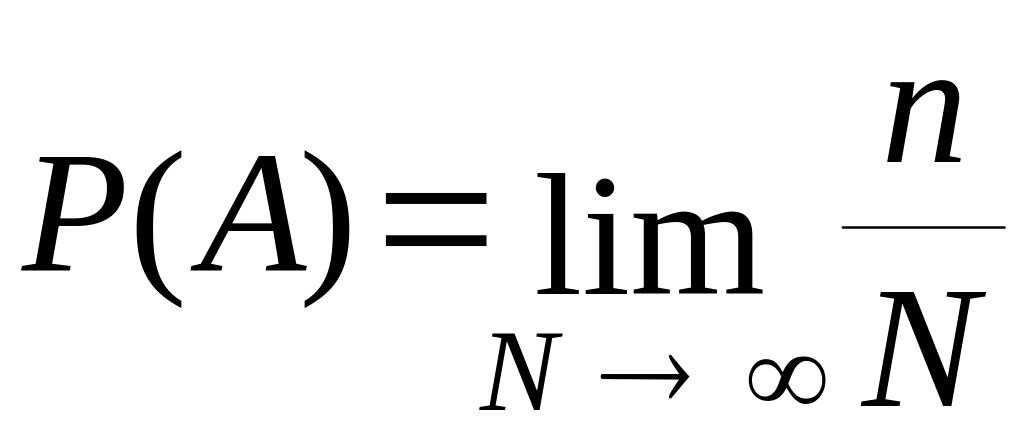
тобто вірогідність події А можна представити як межу відносної частоти події при числі випробувань, прагнучому до нескінченності. Враховуючи, що n ніколи не може перевершити N, то для будь-якої події А його вироятность знаходиться в межах 0  Р (А)  1 і не може бути негативною.

До поняття вірогідності можна підійти і геометричним шляхом. Розглянемо як приклад двомірний випадок. Припустимо, що на площу S впав спортивний снаряд. Визначимо вірогідність попадання снаряда на площу SА як безрозмірне відношення

Представлене таким чином відношення визначає поняття геометричної вірогідності в двовимірному просторі. Аналогічно можна ввести вірогідність для одновимірного, тривимірного і багатовимірного просторів.

Сучасних математиків не задовольняє частотне або геометричне визначення вірогідності, вони віддають перевагу іншому, абстрактнішому, але коректне, що спирається на теорію множин.

Розглянемо деякий експеримент, результат якого залежить від випадковості. Розглядатимемо результати експерименту як елементи деякої множини. Наприклад, при підкиданні гральної кістки можливими результатами можуть бути: 1, 2, 3, 4, 5, 6.., а при підкиданні монети - орел або решка.

Множина, що містить всі можливі результати деякого експерименту називається простором подій (повною групою подій) і позначається символом .

Точки простору подій, тобто можливі результати експерименту, називаються елементарними подіями. У розглянутих прикладах множини містять в собі 6 або 2 елементу.

Будь-якій події А може відповідати деяка підмножина простору подій , а саме безліч тих елементарних подій, при настанні яких відбудеться подія А. Наприклад, якщо А означає, що гральна кістка випаде на непарне число, то подія А відповідає підмножинам простору подій , що містить елементи 1, 3, 5.

Засновником теоретико-множинного числення вірогідності є Колмогоров А.Н. Виділимо систему S підмножин простору подій , для якої встановлені наступні умови:

1. Порожня множина і повний простір подій  повинні бути системи S.

2. Якщо події А1, А2, ... є елементом системи S, то сума і різниці подій таких повинні бути елементами системи S. Система множин, задовольняюча цією умовою називається  - алгеброю.

Отже, подіями є такі підмножини , які є елементами  - алгебра системи S.

В деяких випадках система S містить всі підмножини простору подій , а в інших - лише певні підмножини .

Аксіоматичним шляхом математичне поняття вірогідності введене таким чином. До кожного елементу  -алгебри системи S, тобто кожній події, пов'язаній з даним експериментом, наказує число Р (А), назване вірогідністю даної події, для якого встановлюються наступні обмеження:

1. 0  Р (А)  1 (вірогідність будь-якої події знаходиться в межах

від 0 до 1);

2. Р () = 0, Р() = 1 (вірогідність неможливої події рівна 0,

а вірогідність достовірної події рівна 1);

3) якщо Аi  $ і Аi Aj =  (i  j), то Р (А1 + А2 +...) = Р (А1 )

+ (А2 )+...

тобто вірогідність суми подій, що попарно виключають один одного, співпадає з сумою вірогідності цих подій (див. п. 3.3).

Вищеперелічені умови називаються системою аксіом теорії вірогідності по Колмогорову.

Відзначимо, представлення вірогідності через межу відносної частоти при великій кількості експериментів задовольняє справжнім аксіомам. На підставі цих аксіом вже може бути складена строга математична теорія вірогідності.