Приклад

Визначити, стійка чи рекурсивна ЛДС, імпульсна характеристика (IX) якої має вид дискретної експоненти

Рішення. Підставивши дану IХ в (4.25), отримаємо ряд типу (3.20)

(4.27)

при q= область його збіжності .

У цій області імпульсна характеристика має вигляд затухаючої експоненти, а ЛДС, згідно критерію (4.25), є стійкою.

Поза області збіжності, при |a| 1, ряд (4.27) виявляється розбіжним

а ЛДС, згідно критерію (4.25), нестійкою.

Узагальнюючи даний результат, можна зробити наступні висновки:

- Рекурсивні ЛДС (БИХ-системи) вимагають перевірки на стійкість;

- Імпульсна характеристика стійкою рекурсивної ЛДС має характер затухаючої функції часу.

8. Дискретні перетворення сигналів

 

Крім звичного подання сигналів і функцій у вигляді залежності їх значень від певних аргументів (часу, лінійної або просторової координати тощо) при аналізі й обробці даних широко використовується математичний опис сигналів по аргументах. Можливість такого опису визначається тим, що будь-який як завгодно складний за своєю формою сигнал, що не має нескінченних значень на своєму інтервалі, можна представити у вигляді суми більше простих сигналів, і, зокрема, у вигляді суми найпростіших гармонійних коливань, що виконується за допомогою перетворення Фур'є. Відповідно, математично розкладання сигналу на гармонічні складові описується функціями значень амплітуд і початкових фаз коливань по неперервному або дискретному аргументі. Сукупність амплітуд гармонічних коливань розкладання називають амплітудним спектром сигналу, а сукупність початкових фаз – фазовим спектром. Обидва спектри разом утворюють повний частотний спектр сигналу, що по точності математичного подання тотожний динамічній формі опису сигналу.

Крім гармонічного ряду Фур'є, застосовуються й інші види розкладання сигналів: по функціях Уолша, Адамара, Вейвлета та інших, крім того, існують розкладання по поліномах Чебишева, Лаггера, Лежандра та інших. У ЦОС широко використовується дискретне перетворення Фур'є (ДПФ, discrete Fourier transform) і алгоритм його швидкого обчислення – швидке перетворення Фур'є (ШПФ). Вони дозволяють адекватно описувати в частотних координатах всі, крім самих миттєвих (< 1 с) сигналів; усічені по частоті Фур'є-компоненти описують дані більш правдоподібно, ніж будь-які інші степеневі ряди.

 

7.5.1. Спектр Фур'є неперервних та дискретних сигналів.

 

Нехай   – неперервний сигнал, що задовольняє умові  . Сигнал   у цьому випадку може бути представлений у вигляді інтегрального розкладання по системі комплексних синусоїдальних функцій – інтеграла Фур'є:

.          (1.1)

де   – комплексна функція, що визначає амплітуду та фазову затримку комплексної синусоїди із частотою  : . У загальному випадку ця функція визначена на всій осі частот   і називається вона Фур'є-спектром сигналу  .

У свою чергу Фур'є-спектр   може бути отриманий з вихідного сигналу   за допомогою співвідношення:

                         (1.2)

Співвідношення (1.1), (1.2) являють собою пари інтегральних перетворень Фур'є, причому (1.2) – пряме перетворення Фур'є, (1.1) – іобернене перетворення Фур'є.

Відмітимо, що сигнал   и Фур'є-спектр   – дві взаємнооднозначні характеристики, перша є часовим представленням сигналу, друга – частотним. Часове представлення більш наочне та звичне для повсякденного сприйняття, друге – менш наочне, але винятково корисне при математичному описі перетворень сигналів у лінійних системах з постійними параметрами.

Основні властивості Фур'є-спектра  :

1. Функція   в загальному випадку є комплексною :

.

Функцію  називають амплітудним спектром (іноді магнітудою спектра), вона визначає дійсну амплітуду синусоїди із частотою  , що приймає участь у формуванні сигналу. Функцію   називають фазовим спектром, вона показує фазовий зсув, якому варто піддати комплексну синусоїду частоти   перед підсумовуванням при відновленні вихідного сигналу.

2. Внаслідок дійсності сигналу   функція   має комплексно-спряжену симетрію

,      

,           

3. Енергія спектра Фур'є обмежена й дорівнює енергії вихідного сигналу (рівність Парсеваля):

У теорії безперервних лінійних систем з постійними параметрами широко використовується поняття перетворення Лапласа (s - перетворення):

,                         (1.3)

функції, визначеної на комплексної s- площині:  .

При цьому пряме перетворення Фур'є (1.2) може розглядатися як перетворення Лапласа, обчислене на уявній осі в s-площині:

.

У зв'язку із цим, у літературі часто можна зустріти позначення для Фур'є-спектра –  , в якому є вказівка на те, що це спектр саме неперервного сигналу.

В теорії дискретних лінійних систем замість s-перетворення Лапласа широко використовується поняття Z-перетворення дискретного сигналу

                         (1.4)

Z-перетворення має сенс, для тих значень комплексної змінної z, при яких ряд (1.4) збігається.

Z-перетворення лінійне, завдяки чому воно успішно використовується при описі лінійних дискретних систем. Вихідна послідовність може бути відновлена за допомогою оберненого Z - перетворення :

    

,                        

де С – замкнутий контур, що охоплює все особливі точки функції  .

Спектр Фур'є дискретних сигналів. Спектром Фур'є послідовності  називають комплексну функцію 

                         (1.5)

                                    (1.6)

Вираз (1.6) показує, як вихідна послідовність може бути зібрана з дискретизованих комплексних синусоїд різних частот, узятих з вагами  . Порівняння (1.5) з (1.4) показує, що спектр Фур'є   – є просто Z-перетворенням, обчисленим на одиничній окружності   в комплексній Z-площині. Властивості спектра Фур'є дискретних сигналів подібні до властивостей спектра Фур'є неперервних сигналів. Однак є принципова відмінність. Спектр  періодичний по частоті з періодом  . Тому його значення розглядають на одному періоді – або  , або  .

9.Z - перетворення.

Ефективність частотного аналізу дискретних сигналів істотно зростає, якщо замінити перетворення Лапласа Z - перетворенням. У цьому випадку зображення сигналу X (p), яке представляє собою трансцендентну функцію змінної P = d + jw, замінюється Z - зображенням сигналу X (Z), яке є раціональною функцією змінної Z = x + jy.

Формули Z - перетворення виходять з формули Лапласа (1.6) заміною змінних

epT = Z. (1.7)

Підстановка (1.7) та її похідної

dZ / dp = TepT

в (1.6) приводить до формул прямого і зворотного Z - перетворення

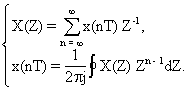 (1.8)

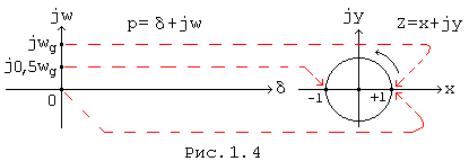
Точки на уявної осі комплексного змінного p = d + jw, тобто точки p = jw, визначають реально частотні характеристики сигналу. Уявної осі відповідає на площині Z одиничне коло, тому що в цьому випадку згідно (1.7)

Z = ejwT =   (1.9)

Тому безперервного росту змінної на уявної осі площині p = d + jw, відповідає багаторазовий обхід одиничному колі на площині z = x + jy (Мал. 1.4). Цим фактом пояснюється, зокрема, та обставина, що інтегрування у формулі зворотного z - перетворення (1.8) здійснюється уздовж одиничному колі площині z замість інтегрування уздовж прямої паралельної уявної площини p.

Враховуючи вищевикладене та формули (1.7), (1.9) можна стверджувати, що ліва полуплоскость змінного p = d + jw відображається на площину одиничного кола змінного z = x + jy, права полуплоскость - на площину z за межами одиничного кола.

Підстановка (1.9) в z - зображення сигналу призводить до спектру цього сигналу, підстановка (1.7) дає зображення по Лапласа.

Приклад. Визначити спектр та побудувати графіки модуля й аргументу спектральної щільності сигналу x (nT) = {a; b} (Мал. 1.5, а).

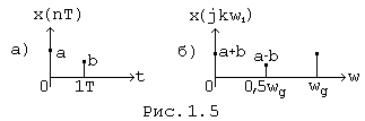
Рішення.

Z - зображення сигналу згідно (1.8)

X (Z) =   x (nT) Zn = x (0T) Z-0 + x (1T) Z-1 = a + bZ-1

Звідси підстановкою (1.9) визначаємо спектр сигналу

X (jw) = a + be-jwT.

Графіки модуля й аргументу спектральної щільності наведені на малюнку 1.6, а, б на інтервалі частот [0; wд].

Поза інтервалу частот [0; wд] частотні залежності повторюються з періодом wд.

Основні теореми Z - перетворення.

Перерахуємо без доведення теореми z - перетворення, які потрібні в наступних розділах.

1. Теорема лінійності.

Якщо x (nT) = ax1 (nT) + bx2 (nT),

то X (Z) = a X1 (Z) + bX2 (Z).

Теорема запізнювання.

Якщо x (nT) = x1 (nT - QT),

то X (Z) = X1 (Z) ZQ.

Теорема про згортку сигналів.

Якщо X (nT) =   x1 (kT) x2 (nT - kT),

то X (Z) = X1 (Z) X2 (Z).

Теорема про примноження сигналів.

Якщо x (nT) = x1 (nT) x2 (nT),

то X (Z) =   X1 (V) X2 (   ) V-1 dV,

де V, Z - змінні на площині Z.

Теорема енергій (рівність Парсеваля).

 x2 (nT) =   X (Z) X (Z-1) Z-1 dZ.

Z - перетворення дискретних сигналів має значення рівне значенню перетворення Лапласа безперервних сигналів.

Дискретне перетворення Фур'є.

Якщо сигнал обмежений у часі значенням tu, а його спектр - частотою wв, то він повністю характеризується кінцевим числом відліків N як в тимчасовій, так і в частотній областях (Мал. 1.7, а, б):

N = tu / T - в тимчасовій області, де T = 1/fд,

N = fд/f1 - в частотній області, де f1 = 1/tu.

Дискретного сигналу відповідає періодичний спектр, дискретного спектру буде відповідати періодичний сигнал. В цьому випадку відліки X (nT) = {X0; X1; ... XN-1} є коефіцієнтами ряду Фур'є періодичної послідовності X (jkw1), період, який дорівнює wд. Відповідно, звіти X (jkw1) = {X0; X1; ... XN-1} є коефіцієнтами ряду Фур'є періодичної послідовності X (nT), період, який дорівнює tu.

Зв'язок відліків сигналу і спектру встановлюється формулами дискретного перетворення Фур'є (ДПФ). Формули ДПФ випливають з формул Фур'є для дискретних сигналів (1.5), якщо безперервну змінну w замінити дискретної змінної kw1, тобто

w ® kw1, dw ® w1.

Після заміни змінної в (1.5) отримаємо

X (jkw1) =   x (nT)   ,

x (nT) =   X (jkw1)   .

Звідси після підстановки w1 = wд / N, T = 2p/wд формули ДПФ приймають остаточний вигляд

X (jkw1) =   x (nT)   - Пряме ДПФ,

x (nT) =   X (jkw1)   - Зворотне ДПФ (1.10)

Сигнал з обмеженим спектром має, строго кажучи, нескінченну довжину в часі і, відповідно нескінченне число відліків і безперервний спектр. Спектр залишиться безперервним, якщо число відліків сигналу обмежити кінцевим числом N. Формули (1.10) в цьому випадку будуть висловлювати зв'язок між N відліками дискретного сигналу та N відліками його безперервного спектру, який можна повністю відновити за його відліками.

Приклад. Визначити відліки спектру сигналу на Рис. 1.5, а.

Тут N = 2 тому X (jkw1) =   x (nT) e-jpkn отже

X (j0w1) =   x (nT) e-j0 = x (0T) + x (1T) = a + b

X (j1w1) =   x (nT) e-jpn = x (0T) e-j0 + x (1T) e-jp a = - b

графік відліків спектру наведено на Рис. 1.5, б, де w1 = wд / N = 0,5 wд.

Сигнал з кінцевим числом відліків N має спектр, який повторює з кінцевою похибкою спектр сигналу з нескінченним числом відліків: спектри співпадають на відлікових частотах kw1 і відрізняються на інших частотах. Відмінність спектрів тим менше, чим більше N. Справді, реальні сигнали мають кінцевою енергією і, отже, починаючи з деякого номера відліку іншими номерами можна знехтувати через їх малості, що не матиме помітного впливу на спектр сигналу.

Приклад. Здійснити дискретизацію експоненціального імпульсу X (t) = Ae-at = 1 e-10t і порівняти спектри вихідного і дискретного сигналів.

Рішення.

Графік сигналу X (t) представлений на Рис. 1.8

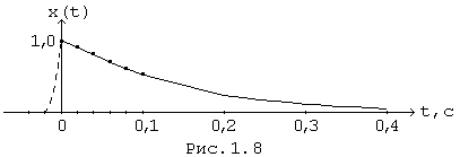
Нехай T = 0,02 с. У цьому випадку плавним сполученням відліків сигналу (штрихова лінія на Рис. 1.8) сигнал відновлюється задовільно хоча помітні спотворення в околиці точки t = 0, тому помилки накладення будуть певним чином впливати на спектральні характеристики.

Нехай tu = 0,4 с. У цьому випадку

N = tu / T = 20.

Розрахунок спектру за формулою прямого ДПФ в точці w = 0 (k = 0) запишеться так

X (j0w1) = 1,0 + 0,8187 + 0,6703 + 05488 + 0,4493 + 0,368 + 0,3012 + 0,2466 + 0,2019 + 0,1653 + 0,1353 + 0,1108 + 0 , 09072 + 0,07427 + 0,06081 + 0,04979 + 0,04076 + 0,03337 + 0,02732 + 0,02237 = 5,41

Істинне значення спектру в точці w = 0 можна визначити знаючи спектр аналогового експоненціального імпульсу

Xa (jw) =   , Отже Xa (j0) =   = 0,1.

щоб порівняти спектри дискретного і безперервного сигналів, дискретний спектр необхідно денорміровать множенням на T, так як формули Фур'є для дискретних сигналів застосовуються в нормованому вигляді. Тому

X (jow1) = 5,41 T = 5,42 ч0, 02 = 0,1082.

Таким чином збіг спектрів Xa (jw) і X (jw) в точці w = 0 цілком задовільний. Деяка неточність пояснюється впливом помилок накладення.

Доречно зауважити, що вибір кроку дискретизації досить контролювати в точках максимальної крутості вихідної функції X (t). У розглянутому прикладі такою точкою є момент часу t = 0.

На закінчення відзначимо, що формули ДПФ спрощують розрахункові процедури за взаємною перетворенню сигналів та їх спектрів, що особливо важливо для технічних систем, що функціонують У реальному масштабі часу. В таких випадках застосовується алгоритм швидкого перетворення Фур'є (ШПФ), заснований на формулах ДПФ. Прискорена процедура розрахунків за алгоритмом ШПФ досягається за рахунок виключення повторних арифметичних операцій, характерних для розрахунків за формулами ДПФ.