7.3. Размерно-ограниченные кристаллические среды.

Дискретность волнового вектора

В настоящее время произ­водится все возрастающее количество устройств и структур, имеющих один или несколько размеров порядка 100 Å или меньше. Естественно, возникает вопрос о влиянии размерного ограничения на свойства фоно­нов в таких наноструктурах и о свойствах фононных взаимодействий в них.

До сих пор мы исследовали свойства фононов или в бесконечном кристалле, либо в кристалле с периодическими условиями. При отсутствии дефектов структуры и примесей фононы являются коллективными возбуждениями, которые описываются на языке блоховских волн. В случае ограничения размера кристалла необходимо учитывать те колебания системы, которые связаны с поверхностными атомами. Для этого случая можно использовать теорему Ледермана, в которой рассматривается зависимость колебательных состояний от размеров колебательной системы, и утверждается, что макроскопический подход применим только в случае, если число решений колебательной системы, связанных с граничными атомами, составляет более половины от общего числа решений. В противном случае приближение бесконечного кристалла некорректно и может вызывать ошибки. Математически основной вывод из теоремы Ледермана можно отразить неравенством: N³/2>6N², где N – число элементарных ячеек вдоль одной из граней куба (колебательная система для простоты имеет кубическую форму). Если учесть, что в элементарной ячейке содержатся не менее одного атома, то для выполнения неравенства колебательная система должна состоять более чем из 1700 атомов. Реальные же нанообъекты, которые представляют собой гетероструктуры, содержат слои, составленные из значительно меньшего числа частиц. В условиях конфайнмента, которые могут быть определены теоремой Ледермана, необходимо учитывать особые свойства колебательных систем, которые начинают проявляться при переходе в нанообласть. Центральной темой этой главы является описание оптических и акустических фононов и их взаимодействий в наноструктурах.

Фононные возбуждения в наноструктурах неизбежно испытывают влияние эффек­та размерного ограничения («конфайнмента»). Это явление в некоторой степени сходно с эффектом запирания электрона в квантовой яме.

Рассмотрим хорошо известную волновую функцию электрона в бесконечно глубокой квантовой яме, имеющей ширину N_za, где N_z – в направлении z, а a – период решетки. Для свободной частицы с эффективной массой m, движение которой в кристалле в направлении z ограничено непроницаемыми барьерами (т.е. барьерами с бесконечной потенциальной энергией) конфайнментные состояния можно получить, решая стационарное уравнение Шрёдингера. Собственные волновые функции ψ_n(z) соответству­ющих энергетических состояний могут быть представлены следующим образом: в направлениях, параллельных границам раздела, — в виде плоских волн, а в направлении z – как связанные состояния частицы в бесконечно глубокой квантовой яме:

.

Здесь k и r – проекции радиус-вектора r и волнового вектора k на плос­кость, параллельную границам раздела, k_г =nπ/N_z , а n=1,2,3.... – нумерует собственные значения энергии:

.

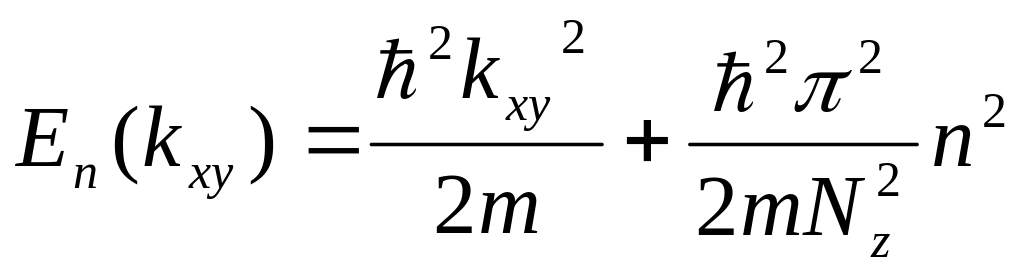Величина А есть площадь границы раздела, по которой нормирована волновая функция электрона. Ясно, что основной эффект размерного ограничения в направлении z состоит в том, что z-компонента волнового вектора ограничена дискретными значениями, кратными π/N_z , что приводит к сокращению фазового пространства (рис. 52).

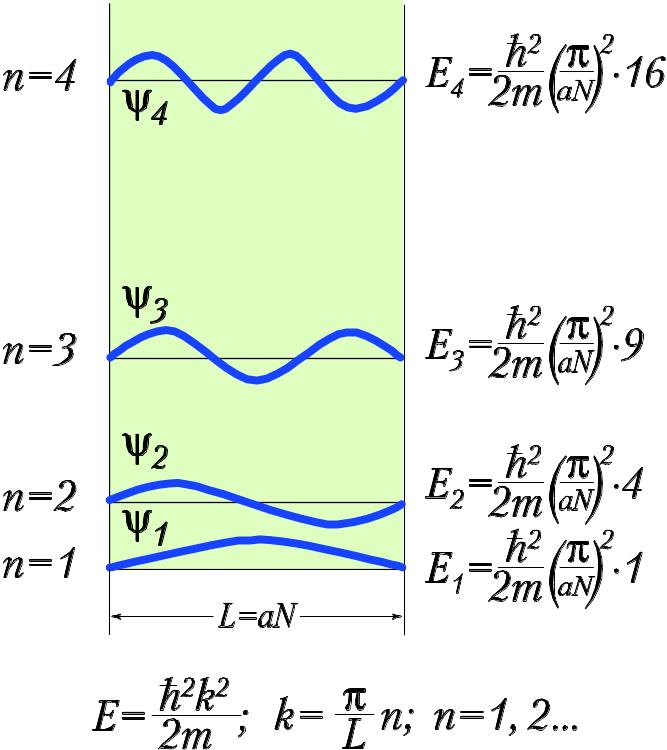
Рис. 52. Волны де-Бройля в одномерном ящике длины L=aN. Энергии собственных состояний растут как квадраты натуральных чисел n.

Таким образом, размерное квантование влияет на электроны в квантовой яме. Это влияние возникает, когда разрешенные энергии электронов в яме соответствуют запрещенным энергиям в барьере (т.е. состояниям запрещенной зоны). Фононы, подобно электронам, также можно представить в виде блоховских волн с дисперсионными соотношениями, дающими зависимость разрешенных энергий (т.е. частот) от блоховского волнового вектора. Поэтому и для фононов в квантовых ямах и сверхрешетках также могут возникать эффекты квантования.

Размерное ограничение фононов приводит к сходным, как и для электрона, ограничениям в фазовом пространстве, накладываемым на волновой вектор фонона q, связанного с граничными условиями равенства нулю смещений атомов на границах раздела. Волновые векторы оптических фононов в диэлектрическом слое толщины d по аналогии с задачей об электроне в бесконечно глубокой квантовой яме также даются выражением q_z = nπ/dN_z. C помощью спектроскопии комбинаци­онного рассеяния света было показано, что волновые векто­ры q_z = nπ/dN_z оптических фононов, находящихся в квантовой яме, образованной десятью монослоями вида AlAs/GaAs/AlAs, настолько чувствительны к изменениям N_z, что изменение толщины ямы все­го лишь на один атомный слой сразу же проявляется в измене­нии q_z! Поэтому фононы в наноструктурах действительно ограничены, и существующие волновые векторы фононов хорошо описыва­ются относительно простыми континуальными моделями фононного конфайнмента. Поскольку эффект размерного ограничения фононов в нано­структурах приводит к сокращению их фазового пространства, очевидно, что в наноструктурах этот эффект будет оказывать влияние как на взаимодействие фононов друг с другом, так и с носителями зарядов.

Возникновение новых оптически активных мод в области акустических колебаний решеток вследствие "фолдинга" из-за наличия сверхпериодичности, возникновение конфайнментных мод, локализованных в соответствующих слоях SL, и появление интерфейсных мод в случае рассмотрения дипольных колебаний многократно обсуждалось в литературе для описания реальных колебательных состояний и получения характеристической информации о SL.