Особенности функции g(), обусловленные различными критическими точками

Тип точки	Обозна-чение	поведение g() вблизи c
		c	c
Минимум	Po	0	 (c2-2)1/2
Седловая точка	P1	 (c2-2)1/2	const
Седловая точка	P2	const	 (c2-2)1/2
Максимум	P3	 (c2-2)1/2	0

Вид функции плотности частот вблизи этих точек показан на рис. 42a. Существует важная теорема Ван-Хова, утверждающая, что в трехмерном случае спектр частот колебаний каждой ветви должен содержать, по крайней мере, точки минимума (P₀) и максимума (P₃) и по трем критическим седловым точкам каждого типа (P₁ и P₂). Важно, что производная на высокочастотном конце спектра должна стремиться к – (критическая точка P₃).

Существование особенностей функции g() является следствием дискретности кристаллической решетки. В трехмерном случае изолированная критическая точка приводит к разрыву лишь производной g(), а не самой функции. Кроме аналитических критических точек существует другие критические точки, которые могут давать более сильные особенности на функции распределения плотности частот. Это относится к тем случаям, когда в критической точке вторая производная по волновому вектору равна нулю. В частности, критические точки объемоцентрированной кубической решетки, для которой дисперсионная формула имеет вид:

,

где i=1/2a_ok_i, и a – постоянная решетки. Уравнения, определяющие критические точки, имеют вид:

cos₁ cos₂ sin₃ = 0

cos₁ sin₂ cos₃ = 0

sin₁ cos₂ cos₃ = 0.

Решение этой системы показывает, что точки (0,0,0), (,,), (/2,/2,/2) являются критическими, причем первые две из них аналитические, последняя – неаналитическая. Эта точка (/2,/2,/2) является точкой пересечения трех взаимно-перпендикулярных плоскостей постоянной частоты ₁=/2, ₂=/2, ₃=/2 и обуславливает появление у функции g() особенности вида ln2|²–1/2_o²|.

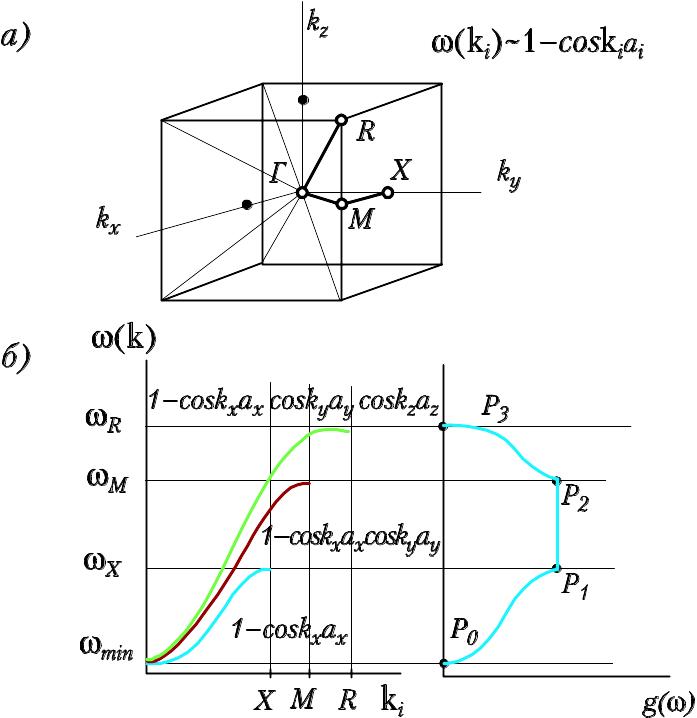
Рис. 35. Появление особенностей Ван-Хова в простой кубической решетке. а) зона Бриллюэна простой кубической решетки и симметричные точки зоны Г, X, M и R. б) дисперсионные зависимости одной ветви, нарисованные для случая направлений (100), (110) и (111), и имеющие приблизительный функциональный вид 1–cos(k_ia_i) для каждого направления k_i. Справа показана получающаяся для этого случая функция плотности состояний g().

На рис. 36 показан спектр собственных частот кристалла меди отдельно для трех ветвей. Он получен путем решения векового уравнения для 5600 значений волнового вектора k, равномерно распределенных по неприводимой 1/48 части зоны Бриллюэна для различных отношений силовых постоянных взаимодействий между атомами. Очевидно, что такое большое количество вычисленных частот дает спектр, в котором отчетливо видны особенности Ван-Хова. Однако в ряде случаев возможна компенсация особенностей функции плотности частот. В трехмерном случае, например, возможна компенсация особенностей, обусловленных минимумом и седловой точкой P₂, а также максимумом и седловой точкой P₁ в различных ветвях.

Существование особенностей функции распределения собственных частот было показано в расчетных спектрах для определенны моделей кристаллов. Однако, окончательно было не ясно, присуще ли наличие критических точек только рассмотренным частным моделям или их наличие носит общий характер. Ответ на этот вопрос дал Ван-Хов, который показал, что существование критических точек в семействе плоскостей постоянной частоты в k-пространстве, а, следовательно, и существование особенностей функции распределения частот является необходимым следствием периодичности решетки в обычном пространстве.

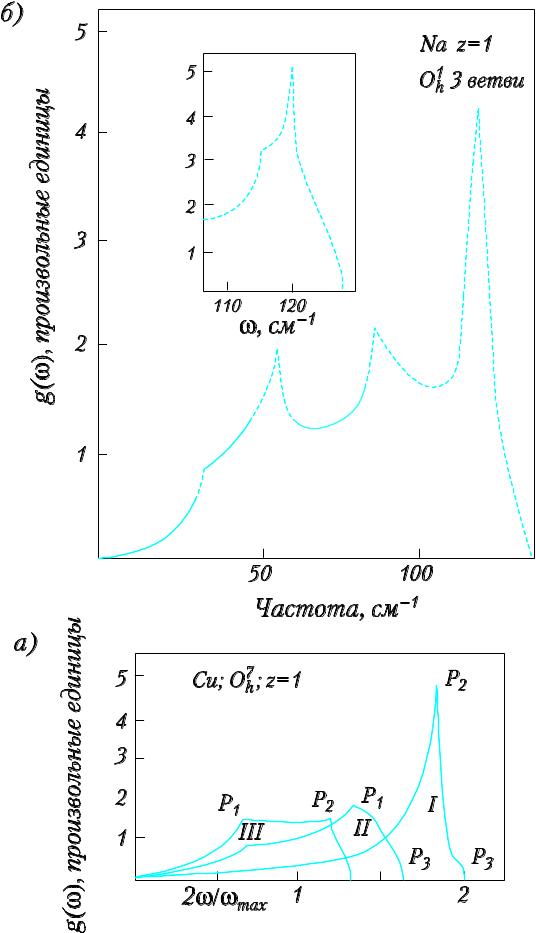
Рис. 36. а) Спектр трех ветвей собственных частот кристалла меди, вычисленный для модели с центральным взаимодействием между ближайшими и следующими за ними соседями. б) Спектр кристалла натрия, рассчитанный для 24.576.000 значений волнового вектора в первой зоне Бриллюэна.

Топологическое обоснование существования аналитических критических точек в двумерном случае состоит в следующем. На рис. 42б показано несколько элементарных ячеек обратного k-пространства. Поскольку дисперсионная зависимость (k₁,k₂) непрерывна и периодична в пространстве волновых векторов k, то в каждой ячейке она должна иметь, по крайней мере, один максимум и один минимум. Пусть расположение максимума в каждой ячейке отмечено знаком , а положение минимума функции (k) – черными кружками. Если максимумы A и B в соседних ячейках соединить произвольной кривой, то на ней будет один минимум, т.е. точка, в которой значение функции (k) принимает меньшее значение, чем в соседних точках. Аналогичные точки есть и на любых других кривых, соединяющих рассматриваемые максимумы A и B. Геометрическое место всех таких точек образует непрерывную кривую, проходящую через абсолютные минимумы C и D в элементарно ячейке обратного пространства. Ясно, что на этой кривой минимумов будет точка, в которой функция (k) принимает наибольшее значение. Эта точка должна быть седловой. Действительно, если двигаться вдоль кривой 4 от C к D, то она будет соответствовать относительному максимуму, а если двигаться по кривой 2 от A к B – относительному минимуму. В двумерной случае в элементарной ячейке обратного пространства имеется две таких седловых точки. Аналогично эвристическое рассмотрение можно провести и в случае трехмерной решетки, что приводит к результатам, установленным Ван-Ховом. В трехмерном случае седловые точки будут двух типов, а дисперсионная функция будет иметь по три точки каждого типа.